DETERMINANTE - Geometria plana / Lista 2

DETERMINANTE
-
Geometria plana / Lista 2
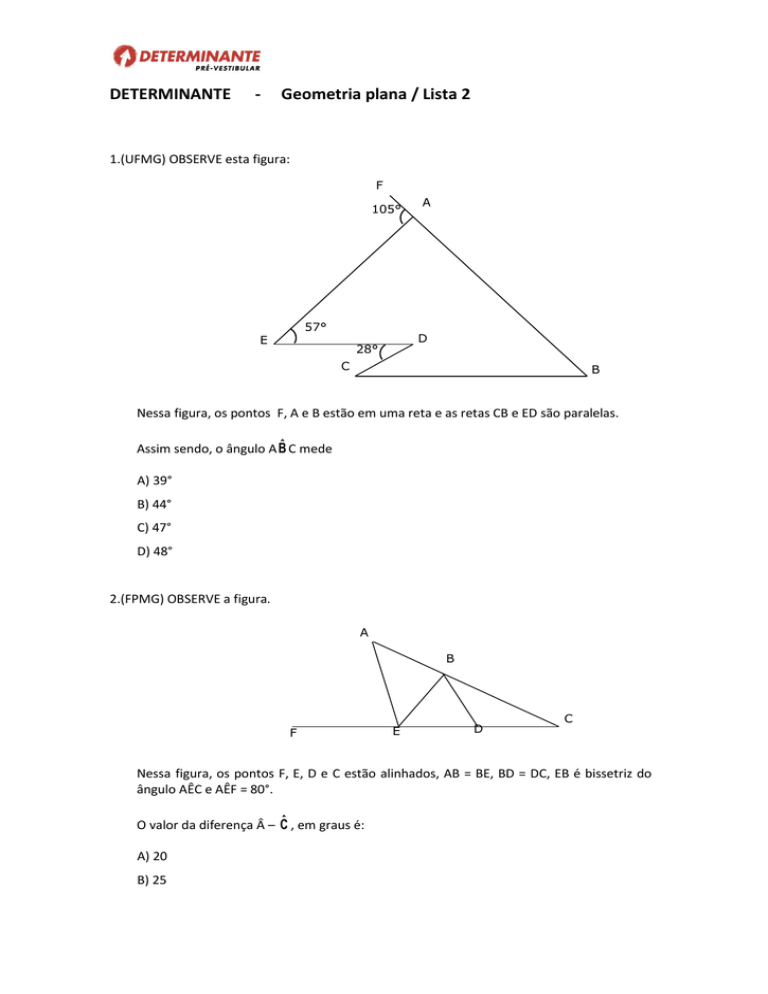
1.(UFMG) OBSERVE esta figura:
F
105°
57°
E
A
D
28°
C
B
Nessa figura, os pontos F, A e B estão em uma reta e as retas CB e ED são paralelas.
Assim sendo, o ângulo A B̂ C mede
A) 39°
B) 44°
C) 47°
D) 48°
2.(FPMG) OBSERVE a figura.
A
B
F
E
D
C
Nessa figura, os pontos F, E, D e C estão alinhados, AB = BE, BD = DC, EB é bissetriz do
ângulo AÊC e AÊF = 80°.
O valor da diferença  – Ĉ , em graus é:
A) 20
B) 25
C) 30
D) 35
3.(UFMG) Nessa figura, AB = AC, BD bissetriz de A B̂ C, CE bissetriz de B Ĉ D e a medida do ângulo
A Ĉ F é 140°.
A medida do ângulo DÊC, em graus, é:
A
E
D
x
A) 20
B) 30
C) 40
140º
B
C
D) 50
E) 60

radianos. A medida do ângulo agudo
7
formado pelas bissetrizes internas dos ângulos Ĉ e B̂ , em radianos, é
4.(UFMG) Em um triângulo ABC, o ângulo  mede
A)

7
B)
2
7
C)
3
7
D)
4
7
E)
5
7
F
5.(UFMG) Com base nos dados da figura, pode-se afirmar que o maior segmento é:
A
E
70°
A) AB
B) AE
65°
C) EC
55°
D) BC
E) ED
65°
°
D
C
B
6.(UFMG) No triângulo ABC tem-se: AB = AC, BD = DE = EC e BÂD = A B̂ D. A medida do ângulo
BÂD é:
A
B
A) 200
B) 22030’
C) 250
D) 300
E) 37030’
D
E
C
7.(UFMG) Num triângulo equilátero ABC, de 8cm de lado, traça-se MN paralelo ao lado BC, de
modo que ele se decomponha num trapézio e num novo triângulo. O valor de MN para o qual
o perímetro do trapézio seja igual ao do triângulo AMN é:
A) 2cm
B) 3cm
C) 4cm
D) 5cm
E) 6cm
8.(UFMG) Sejam O, M, N e P, respectivamente, o ponto de encontro das mediatrizes e os pontos
médios dos lados AB, BC e AC do triângulo ABC. Se os ângulos PÔM, MÔN e NÔP são
proporcionais, respectivamente, aos números 4, 6 e 8, então os ângulos do triângulo ABC
medem, em graus,
A) 30°, 60°, 90°
B) 20°, 70°, 90°
C) 30°, 50°, 100°
D) 20°, 60°, 100°
E) 30°, 45°, 105°
9.(UFMG) Num triângulo retângulo um dos ângulos mede 32o. O ângulo formado pela altura e
mediana relativas à hipotenusa mede:
A) 24°
B) 26º
C) 28°
D) 30°
E) 32°
10.(UFMG)O comprimento de uma mesa retangular é o dobro de sua largura. Se a mesa tivesse
45cm a menos de comprimento e 45cm a mais de largura, seria quadrada.
Assim sendo, a área da mesa é de
A) 1,62m2.
B) 1,45 m2.
C) 1,58 m2.
D) 1,82 m2.
11.Na figura, ABCD é um paralelogramo, EF AD e AE = ED. Se BÂF = 40°, então, B Ĉ D, em graus,
mede
A
B
E
D
A) 100°
B) 110°
C) 120°
D) 130°
F
C
12. As bases MQ e NP de um trapézio medem 42cm e 112cm, respectivamente. Se o ângulo
^
^
MQP mede o dobro do ângulo PNM , então o lado PQ mede, em cm
A) 133
B) 91
C) 77
D) 70
13) (Ufes)
Na figura acima, as retas r e s são paralelas. A somadas medidas dos ângulos indicados
na figura é
a) 180°
b) 270°
c) 360°
d) 480°
e) 540°
14) (Fuvest) Na figura adiante, ABCDE é um pentágono regular. A medida, em graus,
do ângulo ASSINALADO
a) 32°
b) 34°
c) 36°
d) 38°
e) 40°
15) (Puc-rio) Os ângulos internos de um quadrilátero medem 3x - 45, 2x + 10, 2x + 15
e x + 20 graus. O menor ângulo mede:
a) 90°
b) 65°
c) 45°
d) 105°
e) 80°
16) (IBMEC) Considere um hexágono equiângulo (ângulos internos iguais) no qual quatro
lados consecutivos medem 20 cm, 13 cm, 15 cm e 23 cm, conforme figura abaixo. O
perímetro do hexágono, em cm, é
a)
71
b) 68
c) 76
d) 84
e) 99
17) (Fatec) Dada a figura, o ângulo ADC é reto.
Sobre as sentenças
I. O triângulo CDE é isósceles.
II. O triângulo ABE é equilátero.
III. AE é bissetriz do ângulo BÂD.
é verdade que
a) somente a I é falsa.
b) somente a II é falsa.
c) somente a III é falsa.
d) são todas falsas.
e) são todas verdadeiras.
18) (Unifesp) Pentágonos regulares congruentes podem ser conectados, lado a lado,
formando uma estrela de cinco pontas, conforme destacado na figura.
Nestas condições, o ângulo š mede
a) 108°.
b) 72°.
c) 54°.
d) 36°.
e) 18°.
19) (Unesp ) Considere as seguintes proposições:
- todo quadrado é um losango;
- todo quadrado é um retângulo;
- todo retângulo é um paralelogramo;
- todo triângulo eqüilátero é isósceles.
Pode-se afirmar que:
a) só uma é verdadeira.
b) todas são verdadeiras.
c) só uma é falsa.
d) duas são verdadeiras e duas são falsas.
e) todas são falsas.
20) (Fuvest) No retângulo a seguir, o valor, em graus, de α + β é
a) 50
b) 90
c) 120
d) 130
e) 220
Gabarito
1) D
2) A
3) C
4) C
5) A
6) D
7) E
8) D
9) B
10) A
11) B
12) D
13) E
14) C
15) C
16) E
17) E
18) D
19) B
20) D