Laboratório de Física

infinito. Mas na prática realiza-se um numero limitado de medidas, N, por exemplo, resultando
assim numa estimativa do valor verdadeiro e não do valor definitivo. A média de N medidas de
igual confiabilidade de uma grandeza ( X ) será:
X 
Laboratório de Física
Nome:
Data:
EXPERIMENTO Nº 01: MEDIDAS – TEMPO DE REAÇÃO
1)Objetivos : Ao término da atividade deveremos estimar o tempo de reação de um individuo
através de uma medida indireta.
2)Introdução : No laboratório, para alcançar a compreensão de um fenômeno físico é preciso
adotar um procedimento que se possa repetir e variar tantas vezes quantas for necessário, até que
se tenha obtido suficientes dados de observação. Esses dados são, invariavelmente, obtidos
através de processos de medidas. O ato de medir é, portanto, um processo fundamental e nada
trivial na análise experimental de um fenômeno.
Na obtenção de uma medida podem ocorrer dois tipos de erros: o sistemático e o
aleatório. O sistemático deveria ser evitado de todas as formas e, na realidade, nunca deveria
ocorrer em um experimento. Contudo, um instrumento mal calibrado ou defeituoso, um
observador que repete um erro de operação ou interpretação de leitura, ou fatores externos ao
laboratório, como fatores climáticos, são todas fontes de erro sistemático.
O erro aleatório é devido à flutuações dos resultados das medidas em torno de um valor
médio. Essa flutuação de uma medida para outra acarreta uma imprecisão na medida.
Para tanto deve-se ter em mente a diferença entre exatidão e precisão, um valor exato é
aquele que se encontra próximo do verdadeiro resultado de uma medida. Um valor preciso mede
de quanto exato é o resultado, sem referência do “verdadeiro” valor.
Qual é, então o valor de uma grandeza que se quer medir? Essa pergunta nem sempre tem
uma resposta simples, porque geralmente o próprio processo de medida esconde aquilo que se
procura, o valor verdadeiro da grandeza. Há, contudo, situações em que a resposta é facilitada,
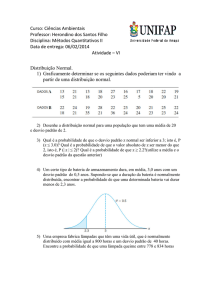
como numa distribuição de medidas com uma freqüência que obedece à curva de
“Gauss”(distribuição normal de freqüências representada na figura abaixo).
18
16
N
( x1  x 2  x3  ...  x N )
x
 n
N
n 1 N
(1)
e X aproxima tanto mais do valor verdadeiro X quanto maior for N. Mas, para todos os efeitos,
considera-se X como a melhor estimativa do valor verdadeiro X .
Devido a natureza estatística do erro aleatório, é impossível determinar seu valor
verdadeiro, sendo somente possível estimar seu valor provável. Para calcular o erro aleatório, é
necessário definir algumas relações.
O desvio X n de uma medida qualquer X n em relação ao valor médio é a diferença entre
o valor de uma medida individual X n da grandeza e seu valor mais provável X , sendo
representado por
X n  X n  X (2)
O desvio padrão , é um dos fatores utilizados pela estatística para indicar a tendência
das medidas de se distribuírem em torno do seu valor mais provával. Pode ser obtido
matemáticamente através da expressão:
 X 
2
 
n
N 1
(3)
O desvio padrão da média (m), tem interpretação análoga à do desvio padrão.
Tendo-se M conjuntos de N medidas de uma grandeza, obtêm-se, para cada conjunto
uma média M . O desvio padrão da média (m), é um dos indicadres da tendência do
conjunto de M médias m de se ditribuírem em torno do seu valor médio. No entanto, m
pode ser obtido a partir do primeiro conjunto de medidas através da expressão:
m 

(4)
N
A partir das definições anteriores, o erro aleatório pode ser estimado através da
expressão
E a  t. m (5)
Onde t é o coeficiente de Student, que pode assunir diferentes valores, dependendo do número de
medidas e da confiabilidade desejada. Por simplicidade será adotado t como sendo 1. Neste caso,
portanto, o erro aleatório provável Ea será numéricamente igual ao desvio padrão da média (m).
Essas definições são de grande valia, na apresentação do resultado de uma medida,
estabelecendo a precisão atribuída ao valor verdadeiro, calculado a partir de N medidas de igual
confiabilidade, logo a maneira de expressar a medida de uma certa grandeza é, portanto,
Freqüência
14
X  X m
12
10
3)Material necessária:
01 régua de 50
01 calculadora
8
xmed
-x
6
0
5
10
15
20
+ x
25
30
35
40
Medidas
Nessa curva X tem propriedades características: é a média aritmética das medidas e é a
mediana, dividindo a área da curva em duas partes iguais.
Pode-se provar que numa distribuição normal de freqüências, a média é o valor
verdadeiro da medida, sempre que o numero de medidas é muito grande, teoricamente deveria ser
4) Procedimento Experimental:
Grandes atletas conseguem correr os 100m em 10 segundos. Na obtenção dessa marca é
extremamente importante a reação do atleta na arrancada. Atirador de tiro ao prato devem reagir
muito rapidamente para acertar o prato lançado com grande velocidade.
Nesta atividade você encontrará o seu tempo de reação, de um modo mais simples. Você
apóia seu antebraço sobre a mesa, de forma que sua mão fique livre. Um colega segura uma
régua verticalmente, de tal modo que o “0” da escala coincida com a parte inferior de sua mão,
conforme o desenho. Ele larga a régua, sem aviso prévio, e você deve segura-la firmemente o
quanto antes.
Repita este procedimento 15 vezes, e anote, cada vez na tabela abaixo, quantos
centímetros a régua percorreu.
5) Andamento das atividades:
a) Determine o valor médio da distância “h” percorrida pela
régua, o desvio padrão , e por fim o desvio padrão da
média da medida (h), justificando o numero de algarismos
significativos.
Esta atividade é um exemplo de medida indireta de
uma grandeza, porque o tempo de reação é obtido a partir de
“h”. Neste caso, é importante saber como expressar o desvio
padrão t, conhecido o desvio h. O desvio padrão t da
medida dos “t” poder ser determinado a partir do desvio
padrão da media dos “h” da seguinte maneira:
2h
g
b) Expresse seu tempo de reação na forma t  t   m .
t 
Medida
1
2
3
4
5
6
7
8
9
10
11
12
X=
t
 h , onde t 
h
X n  X n  X
 X  =
2
n
X n
2