Lista de Exercícios – Circuitos II

Lista de exercícios de Circuitos Elétricos II - Laplace
Prof. Marcelo Semensato
IFG/Jataí
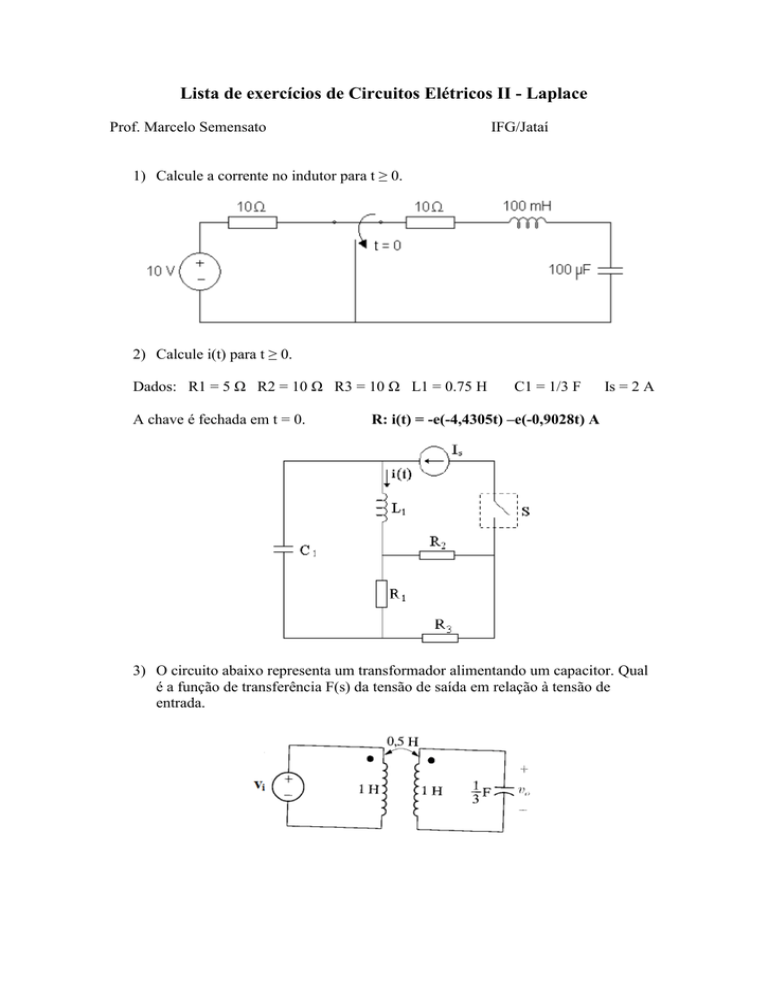
1) Calcule a corrente no indutor para t ≥ 0.
2) Calcule i(t) para t ≥ 0.
Dados: R1 = 5 Ω R2 = 10 Ω R3 = 10 Ω L1 = 0.75 H
A chave é fechada em t = 0.
C1 = 1/3 F
Is = 2 A
R: i(t) = -e(-4,4305t) –e(-0,9028t) A
3) O circuito abaixo representa um transformador alimentando um capacitor. Qual
é a função de transferência F(s) da tensão de saída em relação à tensão de
entrada.
4) Determine as tensões nos nós (V1 e V2).
5) A chave é aberta em t = 0 e, Vs = 16 V, R1 = 12 , R2 = 8 , C1 = 1/36 F e L1 =
1 H, determine ix(t) e vR(t)
R: ix = -0.75e(-2t) -1,25e(-18t) A
6) Calcule v(t) para t ≥ 0
R: v(t) = 27 -9e(-2.67t) V
vR(t) = 6e(-2t) +10e(-18t) V
7) Calcule a tensão no indutor para t ≥ 0
8) Determine i(t) para t ≥ 0. A chave é fechada em t = 0.
Sendo : R1 = 4 Ω, C1 = 1/16 F, L1 = 0,25 H, Vs = 20 V
9) O capacitor encontra-se incialmente descarregado. Em t=0 segundo a chave é
comutada para a posição 1. Em t=100 ms a chave é comutada para 2. Calcule a
corrente iC.
10) Determine i(t) t ≥ 0. A chave é aberta em t = 0.
R1=R2=R3= 6 Ω
C1 = 1/8 F
L1 = 0,5 H
Vs1 = 10 V
Vs2 = 30 V
R: i(t) = 0 A
11) Determine i(t) para t ≥ 0
12) Determine i(t) para t ≥ 0.
R : i(t) = -5e(-t)cos(7t+90º) A
13) Determine vL(t) para t ≥ 0. A chave é aberta em t = 0.
14) Calcular i1(t) para t ≥ 0.
15) O circuito abaixo está operando em regime permanente para t < 0. Em t = 0, a
chave é fechada. Determine o valor de vo(t) para t ≥ 0.
R: v(t) = 9,6e(-t) V
16) Determine a tensão e(t) em função do tempo, sendo i(t) = 10 µ(t) A. Resolver
por nós.
17) Determine i(t) quando a chave é comutada da posição 1 para 2.
R: i(t) = 4 -6e(-2500t) A
18) Determine a corrente i(t) para t ≥ 0, sendo E = 100 V e Ic = 15 A.
19) A chave estava fechada na posição 1 por um longo tempo, em t = 0 segundos a
chave é comutada para a posição 2. Determine a corrente no capacitor para t ≥ 0
segundos.