Exercicios Matemática Pacote

GEOMETRIA PLANA
Prof. Elisete S. O.
EXERCÍCIOS - PARTE 1
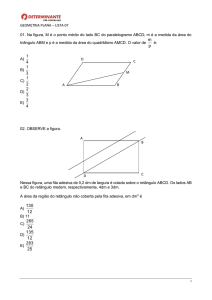
1) (PUC) Se a área do retângulo é de 32 cm2 e os triângulos formados são isósceles, então o
perímetro do pentágono hachurado, em cm, é:
39
a)
b) 10+7 2 c) 10 + 12 2 d) 32 e) 70 2
2
Letra B
h = 4 cm
3 cm
2) (livro) Uma casa ocupa a quarta parte de um terreno de 30 m por 20 m. O restante é usado
como quintal.
600 m2
a) Qual a área total do terreno?
b) Quantas caixas de piso serão necessárias para pavimentar o quintal, sabendo que cada caixa
comporta 1,5 m2 de piso?
300 caixas
3) (livro) Ache a área do setor circular da figura com raio 18 cm e ângulo de 30°:
27  cm2
4) (livro) Ache a área de um retângulo, sabendo que a diagonal mede 10 m e o perímetro 28 m.
48 m2
5) (livro) Numa cozinha de 3 m de comprimento, 2 m de largura e 2,80 m de altura, as portas e
janelas ocupam uma área de 4 m2. Para azulejar as 4 paredes é aconselhável a compra de 10% a
mais da metragem. Calcule a metragem a ser comprada.
26,40 m2
6) (UFRGS) O apótema de um triângulo eqüilátero inscrito em um círculo mede 1 cm. A área,
em cm2, do hexágono inscrito neste círculo é:
Letra D
a) 3
b) 3√ 3 / 2
c) 4√ 3
d) 6√ 3
e) 24√ 3
7) (F.C.CHAGAS) Determine a área da região hachurada nos casos:
a)
Raio = 6 cm
3,25 m2
9
GEOMETRIA PLANA
Prof. Elisete S. O.
b)
2π - 4 cm2
lado=2 cm
9(4- π ) cm2
c)
raio = 3 cm
8) (Provas) Por quanto deve ser multiplicado o raio de um círculo para que sua área triplique?
a) 3 b) 3 c) 6 d) 6 e) 9
Letra B
9) (Provas) Aumentando em 15% uma das diagonais de um losango e a outra em 20%, a área do
mesmo sofrerá um aumento de:
Letra D
a) 28% b) 30% c) 35% d) 38% e) 40%
10) (Provas) O círculo de um setor circular tem raio 6 e ângulo de 100o. A área deste setor é:
a) 6 b) 10 c) 6 π d) 10 π e) π
Letra D
11) (Provas) Determine a área do:
a) Quadrado inscrito em um círculo de 5 m de raio.
50 m2
b) Hexágono regular inscrito em um círculo de raio 4 m.
24 3 m2
c) Triângulo eqüilátero inscrito em um círculo de raio 6 m.
27 3 m2
12) (livro) Ache a área de um triângulo eqüilátero cujo perímetro é igual a 45 dm.
225 3 2
dm
4
13) (livro) A área de um triângulo retângulo é 12 dm 2. Se um dos catetos é
2
do outro, calcule a
3
medida da hipotenusa desse triângulo.
2 13 dm
10
GEOMETRIA PLANA
Prof. Elisete S. O.
14) (livro) Veja as medidas de um terreno pentagonal, na figura.
40 cm
30 cm
30
cm
40 cm
1950 cm2
a) Determine a área da superfície desse terreno.
b) Calcule o preço do terreno se o metro quadrado custa R$ 30,00.
R$ 58.500,00
15) (livro) Ache a área da região colorida da figura. Dados R = 5 m e r = 3 m.
16 π m2
16) (livro) Uma praça é formada de um retângulo de comprimento 100 m e largura 40 m e dois
semicírculos com diâmetro coincidindo com o lado menor
do retângulo.
Em torno da praça será constituída uma calçada de 3 m de largura, cujo preço por metro
quadrado é de R$ 50,00. Calcule o custo total desse projeto, usando π = 3,14. R$ 50.253,00
17) (livro) Calcule a área de um setor circular de amplitude 120o, num círculo de diâmetro 30 cm.
75 π cm2
18) (livro) Dois círculos concêntricos, tem raios de 50 cm e 40 cm, conforme a figura. Calcule a
área da superfície entre os dois setores circulares.
75 π cm2
11
GEOMETRIA PLANA
Prof. Elisete S. O.
19) (livro) Calcule a área de um quadrado inscrito numa circunferência de 3 cm de raio.
18 cm2
20) (livro) Na circunferência de raio 2 cm está inscrito num hexágono regular. Qual é a área desse
polígono?
6 3 cm2
21) (livro) Uma circunferência tem 10 cm de raio. Determine:
a)A medida do lado e medida do apótema do quadrado inscrito na circunferência. 10 2 cm e 5 2 cm
b)A medida do lado e a medida do apótema do hexágono regular inscrito na circunferência.
10cm e
5 3 cm
c)A medida do lado e a medida do apótema do triângulo eqüilátero inscrito na circunferência.
10 3 cm e 5cm
22) (livro) Determinar o raio da circunferência inscrita no hexágono regular cujo lado mede 4 cm.
2 3 cm
23)(livro) Uma estrela de seis pontas, regular, é formada por 2 triângulos eqüiláteros entrelaçados. A
razão entre a área de um dos triângulos e a área da estrela vale:
a) 1 b) ½ c) ¾ d) 1/6 e) 2/3
Letra C
**************************************************************
SIMULADO
1)
Em um restaurante, qual família come mais pizza: aquela que pede uma grande de 43 cm de diâmetro
ou aquela que pede duas médias de 30 cm de diâmetro?
2)
Um triângulo inscrito em uma circunferência, tem apótema 4 cm. Encontre a área desse círculo.
3)
As diagonais de um losango medem juntas 30 cm e a medida de uma é o dobro da outra. Calcule a área
desse losango.
4)
Uma escola tem seus canteiros de forma geométrica. Um deles é o trapézio abaixo. Encontre sua área e
seu perímetro.
5m
4m
5)
8m
Encontre a área da figura abaixo, use 3,14.
8 cm
6 cm
12 cm
3 cm
12
GEOMETRIA PLANA
Prof. Elisete S. O.
6)
Um quarto possui 7 m de comprimento, 5m de largura e 3m de altura, tendo uma porta de 1m por 2m e
uma janela quadrada de 1m de lado. Deseja-se pintar as quatro paredes internas e o teto do quarto,
2
excetuando-se a janela, a porta e o chão. A área a ser pintada (m ) é?
7)
O retângulo da bandeira do Brasil, cuja externa ao losango é pintada de verde, mede 2 m de
comprimento por 1,40 m de largura. Os vértices do losango estão distantes das laterais 17 cm, e o
círculo azul tem raio 35 cm. Para transformar metros para cm multiplique por 100, assim a resposta será
2
em cm . Qual a área da região verde?
8) Encontre a área da parte colorida, na figura abaixo, sendo os diâmetros 8 cm e 2 cm:
9) Um cavalo se encontra preso num cercado de pastagem, cuja forma é um quadrado, com lado
medindo 50 m. Ele está amarrado a uma corda de 40 m que está fixada num dos cantos do
quadrado. Use π = 3,14 e calcule a área do quadrado que o cavalo não conseguirá alcançar.
10) A diferença entre os perímetros de dois quadrados é 32m e a diferença entre as áreas é de
176 m2. Calcule as medidas dos lados desses quadrados.
11) Calcule a área de um losango, cujo perímetro mede 120 cm e a diagonal maior 48 cm.
Boa Prova.
13
GEOMETRIA ESPACIAL
Prof. Elisete S. O.
EXERCÍCIOS - PARTE 2
1) Um prisma triangular regular tem aresta lateral de 9 cm e aresta da base 4cm. Determine:
a) a área da base
b)a área lateral c) a área total d) o volume
a) 4 3 cm2 b) 108 cm2 c) 108 + 8 3 cm2
d) 36 3 cm2
2) Calcule o volume de ar contido em um galpão com a forma e dimensões dadas pela figura a
seguir:
384 m3
3) (UFRGS) Deseja-se elevar em 20cm o nível de água da piscina de um clube. A piscina é
retangular, com 20m de comprimento e 10m de largura. A quantidade de litros de água a ser
acrescentada é:
Letra D
a) 4000 b) 8000 c) 20000 d) 40000 e) 80000
4) Num paralelepípedo retângulo a soma das medidas das arestas é igual a 36 cm. Se estas
medidas estão em PA, calcule a área total do paralelepípedo, sabendo que seu volume é 15
cm3.
46 cm2
5) (PUCRS) Um cubo tem 96m2 de área total. Em quanto deve ser aumentada a sua aresta para
que seu volume se torne igual a 216m3?
2m
6) (PUCRS) Selecionando-se um cubo segundo duas arestas opostas, conforme a figura, obtém-se
um retângulo de 6 2 m2 de área. A diagonal desse cubo, em m, mede:
a) 18 b) 6 6 C) 2 3 D) 2 2 E) 3 2
Letra
E
7) Um prisma hexagonal regular lateral tem aresta 6 3 cm e a aresta da base 2 cm. Encontre seu
volume.
108 cm3
8) Uma pirâmide triangular regular tem todas as arestas iguais a 6 cm. Determine:
a) o apótema da base e da pirâmide
b) a altura da pirâmide
c) a área total e o volume
a) 3 cm e 3 3 cm
b) 2 6 cm
c) 36 3 cm2 e 18 2 cm3
14
GEOMETRIA ESPACIAL
Prof. Elisete S. O.
9) Determine o volume de uma pirâmide, cuja planificação é:
16
3
cm3
3 2 cm
2 cm
10) A altura de uma pirâmide hexagonal regular mede 12 cm e o apótema da base mede 5 cm.
Determine a área total da pirâmide.
108 3 cm2
11) Em uma pirâmide quadrangular regular, a área da base é 256 dm2 e a área lateral é 320 dm2.
Ache a altura da pirâmide.
6 dm
12) O volume de um cilindro eqüilátero é 54π cm3. Qual a sua área total.
54π cm2
13) Calcule o volume do sólido gerado pela rotação de 360o do retângulo da figura em torno do eixo y.
Y ( cm)
6
60π cm2
1
X (cm)
2
4
14) A carga de uma caneta esferográfica tem 2 mm de diâmetro e 10 cm de altura. Se uma pessoa
gasta mais ou menos 10 mm3 de tinta por dia, quanto tempo a carga vai durar?
31 dias
15) Calcule o volume do cilindro reto inscrito num cubo cujo volume é 64 cm3.
16π cm3
16) O que acontece com o volume de um cilindro reto se dobrar o raio de sua base e dividirmos a sua
altura por dois?
Dobra de valor
17) A área de um cone circular reto é 15π m2 e a área total é 24π m2. Calcule a medida do raio do cone.
18) Um cone reto tem 40 cm de altura e 30 cm de raio de base. Ache:
a) a área total
b) o volume
a) 2400 π cm2
3m
b) 12000 π cm3
19) Calcule o volume e a área da esfera inscrita num cubo cuja área total é 216 m2.
36π cm2 e 36π cm3
20) Se a aresta de um cubo inscrito numa esfera mede 2 cm, então a área desta esfera mede, em cm2:
a) 16 π
b) 14 π
c) 12 π d) 10 π
e) nda
Letra C
21) Em um cone circular reto de 18 cm de altura, inscreve-se uma esfera de 5 cm de raio. Determine o
3
volume do cone.
150π cm
22) (PUCRS) Se um prisma quadrangular regular tem área total igual a 10 vezes a área da base, então
a razão entre a sua altura e a aresta da base é:
Letra D
a) ½
b) 1 c) 3/2 d) 2
e) 3
15
16