ESPAÇOS VETORIAIS EUCLIDIANOS Produto interno - ICEB-UFOP

UNIVERSIDADE ESTADUAL DE MATO GROSSO DO SUL – UEMS
ESPAÇOS VETORIAIS EUCLIDIANOS
Produto interno em espaços vetoriais
Estamos interessados em formalizar os conceitos de comprimento de um vetor e
ângulos entre dois vetores. Esses conceitos permitirão uma melhor compreensão do que
seja uma base ortogonal e uma base ortonormal em um EV e, principalmente, nos darão
a noção de “medida” que nos leva a precisar conceitos como o de área, volume,
distância, etc.
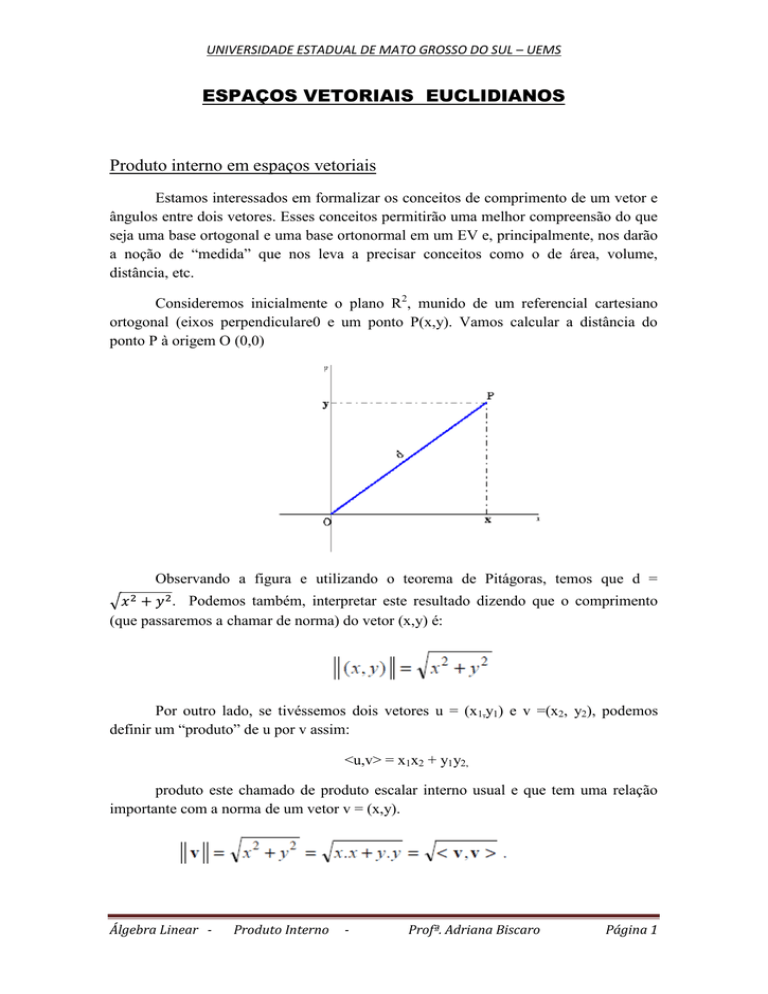
Consideremos inicialmente o plano R2, munido de um referencial cartesiano
ortogonal (eixos perpendiculare0 e um ponto P(x,y). Vamos calcular a distância do
ponto P à origem O (0,0)
Observando a figura e utilizando o teorema de Pitágoras, temos que d =
. Podemos também, interpretar este resultado dizendo que o comprimento
(que passaremos a chamar de norma) do vetor (x,y) é:
Por outro lado, se tivéssemos dois vetores u = (x1,y1) e v =(x2, y2), podemos
definir um “produto” de u por v assim:
<u,v> = x1x2 + y1y2,
produto este chamado de produto escalar interno usual e que tem uma relação
importante com a norma de um vetor v = (x,y).
Álgebra Linear -
Produto Interno
-
Profª. Adriana Biscaro
Página 1
UNIVERSIDADE ESTADUAL DE MATO GROSSO DO SUL – UEMS
Se, ao invés de trabalharmos no R2, estivéssemos trabalhando no R3 (munidos de
um referencial cartesiano ortogonal), teríamos encontrado uma expressão similar para o
produto escalar:
E a mesma relação com a norma de um vetor v = (x,y,z)
Voltando ao caso do plano, se tivéssemos trabalhando com um referencial não
ortogonal (eixos não perpendiculares), e quiséssemos calcular a distância da origem até
um ponto P (cujas coordenadas em relação ao referencial fossem (x,y)), teríamos,
usando o Teorema de Pitágoras:
Obseve que, se usássemos o produto escalar
neste caso não valeria a relação
seguinte regra para o produto:
=
=
, mas ela passaria a valer se usássemos a
Portanto, novamente a noção de distância poderia ser dada a partir de um
produto interno de vetores. Concluímos destes exemplos, que o processo usado para se
determinar “medidas” num espaço pode variar e, em cada caso, precisamos ser bem
claros sobre qual produto interno estamos trabalhando.
Álgebra Linear -
Produto Interno
-
Profª. Adriana Biscaro
Página 2
UNIVERSIDADE ESTADUAL DE MATO GROSSO DO SUL – UEMS
Definição: Seja V um EV real. Um produto sobre V é uma função f: VxV  R
que a cada par de vetores v1 e v2, associa um número real, denotado por <v1, v2>, e que
satisfaz as seguintes propriedades:
P1 u.v = v.u
P2 u. (v + w) = u.v + u. w
P3 (αu).v = α(u.v) para todo real α
P4 u.u ≥ 0 e u.u = 0 se, e somente se, u = 0.
Exemplo:
1) No espaço vetorial V = R2, a função que associa a cada par de vetores
u = (x1, y1) e v= (x2, y2) o número real u.v = 3x1x2 + 4y1y2 é um produto interno.
2) O número u.v = 2x1x2 + y12y22 sendo u = (x1, y1) e v = (x2, y2) não define no R2
um produto interno.
Álgebra Linear -
Produto Interno
-
Profª. Adriana Biscaro
Página 3
UNIVERSIDADE ESTADUAL DE MATO GROSSO DO SUL – UEMS
Exercícios:
1) Em relação ao produto interno usual do R2, calcular u.v, sendo dados:
a) u = (-3,4) e v = (5,-2)
b) u = (6,-1) e v = (1/2, -4)
c) u = (2,30 e v =(0,0)
2) Para os mesmos vetores do exercício anterior, calcular u.v em relação ao
produto interno: u.v = 3x1x2 + 4y1y2.
3) Consideremos o R3 munido do produto interno usual. Sendo v1 = (1,2,-3), v2
=(3,-1,-1) e v3 = (2,-2,0) do R3, determinar o vetor u tal que u.v1 = 4, u.v2 = 6
e u.v3 = 2.
4) Seja V = {f: [0,1]  R; f é contínua} o EV munido do produto interno:
Determinar h1. h2 e h1.h1, tais que h1, h2 ∈ V e h1(t) = t e h2(t) = t2.
Espaço Vetorial Euclidiano
Um EV real, de dimensão finita, no qual está definido um produto interno é um
EV euclidiano.
Módulo de um Vetor
Dado um vetor v de um EV euclidiano V, define-se módulo, normal ou
comprimento de v o número real não-negativo, indicado por |v|, definido por:
|v| =
Se u = (x1,y1,z1) ∈ R3 , tem-se:
|u| =
=
Distância entre dois vetores
Chama-se de distância entre dois vetores (ou pontos) u e v o número real
representado por d(u,v) e definido por:
d(u,v) = |u-v|
Sendo u = (x1,y1,z1) , v = (x2,y2,z2)∈ R3 com produto interno usual, tem-se:
Álgebra Linear -
Produto Interno
-
Profª. Adriana Biscaro
Página 4
UNIVERSIDADE ESTADUAL DE MATO GROSSO DO SUL – UEMS
d(u,v) = |x1 – x2, y1-y2, z1 – z2|
d(u,v) =
Observações:
1) Se |v| = 1 , isto é, v.v = 1, o vetor v é chamado vetor unitário, diz-se que V
está Normalizado.
2) Todo vetor não nulo v ∈ V pode ser normalizado, fazendo:
Observemos que:
E, portanto,
é unitário.
Exemplo: Considerando V = R3 com o produto interno v1.v2 = 3x1x2 + 2y1y2 +
z1z2, sendo v1= (x1, y1,z1) e v2= (x2, y2,z2). Dado o vetor v = (-2,1,2) ∈ R3, em
relação a esse produto interno, determine o vetor u, normalizando v:
Propriedades do Módulo de um Vetor
Seja V um EV euclidiano, tem-se:
I. │ v│≥ 0, ∀ v ∈ V e │v= 0, se, e somente se, v = 0.
II. │αv│= │α││v│, ∀v∈ V, ∀α∈ R
Demonstração:
| αv| =
Álgebra Linear -
=
Produto Interno
= |α|.
-
= |α|.|v|
Profª. Adriana Biscaro
Página 5
UNIVERSIDADE ESTADUAL DE MATO GROSSO DO SUL – UEMS
III. │u.v│≤│u││v│, ∀u,v∈ V
Se u ou v = 0 vale a igualdade:
|uv| = |u|.|v| = 0
Se nem u, nem v são nulos, para qualquer α
(u + αv).(u + αv)
R vale a desigualdade:
0
Pelo axioma P4, Efetuando o produto interno, vem:
u.u + u.( αv) + (αv.u) + α2(v.v)
0
ou,
|v|2 α2 + 2(u.v) α + |u|2
0
Obtivemos assim, um trinômio do 2º grau em α (pois |v|2 ≠ 0), que deve ser
positivo para qualquer valor de α. Como o coeficiente de α2 é sempre positivo, o
discriminante deve ser negativo ou nulo.
(2u.v)2 – 4|v|2 |u|2
2
2
2
4(u.v) - 4|v| |u|
(u.v)2
0
0
|v|2 |u|2
Considerando a raiz quadrada positiva de ambos os membros dessa
desigualdade, vem:
│u.v│≤│u││v│
Essa desigualdade é conhecida com o nome de Desigualdade de Schwarz ou
Inequação de Cauchy-Schwarz.
IV. │u+v│≤│u│+│v│,∀u,v ∈ V
Demonstração
|u+v| =
|u + v| =
|u+v|2 = |u|2 +2(u.v) + |v|2
Mas:
u.v ≤│u.v│≤│u││v│
logo,
|u+v|2 ≤ |u|2 +2|u||v| + |v|2
Ou:
Álgebra Linear -
Produto Interno
-
Profª. Adriana Biscaro
Página 6
UNIVERSIDADE ESTADUAL DE MATO GROSSO DO SUL – UEMS
|u+v|2 ≤ (|u| + |v|)2
Ou ainda,
│u+v│≤│u│+│v│
Ângulos de dois Vetores
Seja V um EV munido com um produto interno. O ângulo θ entre dois vetores
u, v ∈ V é tal que:
Exercícios:
1. Consideremos o R3 com o produto interno usual. Determinar a componente c do
vetor v = (6, -3,c) tal que |v| = 7.
2. Seja o produto interno usual no R3 e no R4. Determinar o ângulo entre os seguintes
pares de vetores:
a) u = (2,1,-5) e v = (5,0,2)
b) u =(1,-1,2,3) e v = (2,0,1,-2)
5. Seja V um EV euclidiano e u, v ∈ V. Determinar o cosseno do ângulo entre os
vetores u e v, sabendo que |u| = 3, |v| = 7 e |u +v| = 4 .
Álgebra Linear -
Produto Interno
-
Profª. Adriana Biscaro
Página 7
UNIVERSIDADE ESTADUAL DE MATO GROSSO DO SUL – UEMS
Álgebra Linear -
Produto Interno
-
Profª. Adriana Biscaro
Página 8
UNIVERSIDADE ESTADUAL DE MATO GROSSO DO SUL – UEMS
Vetores ortogonais
Seja v um EV euclidiano. Diz-se que dois vetores u e v de V são ortogonais, e se
representa por u v, se, e somente se, u.v = 0.
Exemplo: Seja V = R3 um EV euclidiano em relação ao produto interno (x1, y1).(x2, y2)
= x1x2 +2y1y2. Em relação a este produto interno, os vetores u = (-3,2) e v = (4,3) são
ortogonais, pois:
u.v = -3.(4) +2.(2).(3) = 0
Observações:
1) O vetor 0 ∈ V é ortogonal a qualquer v ∈ V.
0.v = 0
2) Se u v, então α u v para todo α∈ R.
3) Se u1 v e u2 v, então (u1 + u2) v.
Conjunto Ortogonal de Vetores
Seja V um EV euclidiano. Diz-se que um conjunto de vetores {v1, v2, ...,vn} V
é ortogonal se dois vetores quaisquer, distintos, são ortogonais, isto é, vi. vj = 0 para i≠j.
Exemplo:
No R3, o conjunto {(1,2,-3), (3,0,1), (1,-5,-3)} é ortogonal em relação ao produto
interno usual, pois:
(1,2,-3). (3,0,1) = 0
(1,2,-3) .(1,-5,-3) = 0
(3,0,1) . (1,-5,-3) = 0
Álgebra Linear -
Produto Interno
-
Profª. Adriana Biscaro
Página 9
UNIVERSIDADE ESTADUAL DE MATO GROSSO DO SUL – UEMS
Teorema:
Um conjunto ortogonal de vetores não-nulos A = {v1, v2,...,vn} é Linearmente
Independente (LI).
De fato:
Considerando a igualdade:
a1v1 + a2v2 + ...+ avn = 0
Multiplicando o produto interno de ambos os lados da igualdade, temos:
(a1v1 + a2v2 + ...+
avn) vi = 0vi
Ou,
a1(v1.vi) + ...ai(vi.vi) + ...+ a(vn.vi)= 0
Como A é ortogonal, vj . vi = 0 para j≠ i e vi.vi ≠ 0, pois vi ≠ 0. Então ai(vi.vi) = 0 implica
ai = o para i = 1, 2,3...n. Logo, A = {v1, v2,...,vn} é LI.
Base Ortogonal
Uma base {v1, v2,...,vn} de V é ortogonal se os seus vetores são dois a dois
ortogonais.
Assim, se dimV = n, qualquer conjunto de n vetores não-nulos e dois a dois
ortogonais, constitui uma base ortogonal.
Poe exemplo, o conjunto do exemplo {(1,2,-3), (3,0,1), (1,-5,-3)} é uma base ortogonal
do R3.
Álgebra Linear -
Produto Interno
-
Profª. Adriana Biscaro
Página 10
UNIVERSIDADE ESTADUAL DE MATO GROSSO DO SUL – UEMS
Base Ortonormal
Uma base B = {v1, v2,...,vn} de um EV euclidiano V é ortonormal se B é
ortogonal e todos seus vetores são unitários, isto é:
Exemplo:
Em relação ao produto interno usual, o conjunto:
1) B = {(1,0), (0,1)} é uma base ortonormal do R2 (é a base canônica).
2) B= {( ,
} é também uma base ortonormal do R2.
3) B = {(1,0,0), (0,1,0), (0,0,1)} é uma base ortonormal do R3 (é a base canônica).
4) B = {u1, u2, u3} sendo u1 = ( ,
; u2 = ( ,
, u3= (0,
,
é
também uma base ortonormal do R3.
Como vimos, o processo que transforma V em
chama-se normalização de v.
Assim, uma base ortonormal sempre pode ser obtida de uma base ortogonal,
normalizando cada vetor.
Exemplo:
A base B = {v1, v2,v3}sendo v1 = (1,1,1), v2 = (-2,1,1) e v3 – (0,-1,1) é ortogonal em
relação ao produto interno usual. Normalizando cada vetor, obtemos:
Álgebra Linear -
Produto Interno
-
Profª. Adriana Biscaro
Página 11
UNIVERSIDADE ESTADUAL DE MATO GROSSO DO SUL – UEMS
Processo de Ortogonalização de Gram-Schmidt
Para entendermos o processo de ortogonalização de Gram-Schmidt é necessário, termos
uma noção de projeção ortogonal.
Projeções ortogonais de vetores
Em muitas aplicações é importante “decompor” um vetor u na soma de dois
componentes, um paralelo a um vetor não-nulo especificado a e o outro perpendicular a
a. Se u e a são posicionados com seus pontos iniciais coincidindo com um ponto Q,
podemos decompor o vetor u, da seguinte forma: Baixamos uma perpendicular da ponto
de u para a reta ao longo de a e construímos o vetor w1 de ao pé desta perpendicular.
Em seguida tomamos a diferença
w2 = u – w1
Conforme indicado na figura, o vetor w1 é paralelo ao vetor a e w2 é perpendicular ao
vetor a e
w1 + w2 = w1 + (u – w1) = u
O vetor w1, chamdo projeção ortogonal de u sobre a, ou então componente vetorial
de u ao longo do vetor a, é denotado por proja u.
O vetor w2 é chamado componente vetorial de u ortogonal ao vetor a. Como
w2 = u – w1 , este vetor pode ser escrito com a notação:
w2 = u – proja u.
Teorema: Se u e a são vetores em R2 ou R3 e se a≠ 0, então:
Álgebra Linear -
Produto Interno
-
Profª. Adriana Biscaro
Página 12
UNIVERSIDADE ESTADUAL DE MATO GROSSO DO SUL – UEMS
Demonstração:
Sejam w1 = proja u e w2 = u – proja u. Como w1 é paralelo a a, deve ser um múltiplo
escalar de a, e portanto pode ser escrito na forma w1 = ka. Assim:
u = w1+ w2 = ka + w2
Tomando o produto escalar de a, com ambos os lados da equação anterior, temos:
u .a = ( ka + w2).a = k
+ w2.a
Mas w2.a = 0, pois w2 é perpendicular a a; portanto dá:
Como proja u = w1 = ka, obtemos:
Seja W um subespaço de dimensão finita de um espaço com produto interno V.
a) Se {v1, v2,...,vr} é uma base ortonormal de W e u é um vetor qualquer de V,
então:
projw u =
b) Se {v1, v2,...,vr} é uma base ortogonal de W e u é um vetor qualquer de V, então:
projw u =
Encontrando uma base ortogonal
Teorema: Cada espaço vetorial não-nulo de dimensão finita possui uma base
ortonormal.
Prova: Seja V um espaço vetorial não-nulo de dimensão finita com produto interno e
suponha que {u1, u2,...,un} é uma base de V. É suficiente mostrar que V tem uma base
ortogonal, pois os vetores da base ortogonal podem ser normalizados para produzir uma
base ortonormal de V. A seguinte sequencia de passos irá produzir uma base ortogonal
{v1,v2,...,vn} de V.
Passo 1: Seja v1 = u1.
Passo2: Conforme ilustrado, nós podemos obter um vetor v2 que é ortogonal a v1
tomando a componente de u2 que é ortogonal ao espaço W1 gerado por v1:
Álgebra Linear -
Produto Interno
-
Profª. Adriana Biscaro
Página 13
UNIVERSIDADE ESTADUAL DE MATO GROSSO DO SUL – UEMS
v2 = u2 – projw1u2 = u2 -
Passo 3: Para construir um vetor v3 que é ortogonal a ambos v1 e v2, calculamos a
componte de u3 que é ortogonal ao espaço W2 gerado por v1 e v2.
v3 = u3 – projw2 u3 = u3 -
Passo 4: Para determinarmos um vetor v4 que é ortogonal a v1, v2 e v3, calculamos a
componente de u4 que é ortogonal ao espaço W3 gerado por v1, v2, e v3.
v4 = u4 – projw3 u4 = u4 -
-
Continuando desta maneira, nós iremos obter, depois de n passos, um conjunto
ortogonal de vetores {v1, v2,...,vn}. Como V trem dimensão n e conjuntos ortogonais são
LI, o conjunto {v1, v2,...,vn} é uma base ortogonal de V.
A construção passo a passo acima para converter uma base arbitrária numa base
ortogonal é chamada processo de Gram-Schmidt.
Exemplo:
Considere o espaço vetorial R3 com o produto interno euclidiano. Aplique o processo de
Gram-Schmidt para transformar os vetores de base u1 = (1,1,1), u2 = (0,1,1), u3 =
(0,0,1) em uma base ortogonal {v1, v2,v3}; depois normalize os vetores da base
ortogonal para obter uma base ortonormal {q1, q2, q3}.
Álgebra Linear -
Produto Interno
-
Profª. Adriana Biscaro
Página 14
UNIVERSIDADE ESTADUAL DE MATO GROSSO DO SUL – UEMS
Exercícios:
1. Suponha que R3 tem o produto interno euclidiano. Use o processo de GramSchmidt para transformar a base {u1, u2,u3} em uma base ortonormal.
a) u1 = (1,1,1) u2 = (-1,1,0) e u3 = (1,2,1)
2. Seja V = R3 e o produto interno (x1, y1, z1).(x2, y2,z2) = 2x1x2 + 3y1y2 + z1z2.
Determinar um vetor unitário simultaneamente ortogonal aos vetores u = (1,2,1)
e v = (1,1,1).
3. Construir, a partir do vetor v1 = (1,-2,1), uma base ortogonal do R3 relativamente
ao produto interno usual e obter, a partir dela, uma base ortonormal.
4. O conjunto B = {(1,-1), (2,b)} é uma base ortogonal do R2 em relação ao
produto interno: (x1, y1).(x2, y2) = 2x1x2 + y1y2. Calcular o valor de b e
determinar , a partir de B, uma base ortonormal.
5. Em relação ao produto interno usual, determinar uma base ortonormal do
seguinte subespaço vetorial do R3: S = {(x,y,z) ∈R3/ x + y- z = 0}
6. Mostre que se f = f(x) e g = g(x) duas funções contínuas em C[a,b] e defina
=
Álgebra Linear -
é um produto interno em C[a,b].
Produto Interno
-
Profª. Adriana Biscaro
Página 15