PROFESSORA: KARINE WALDRICH 1 ICMS MA – LÓGICA E

PROFESSORA: KARINE WALDRICH
ICMS MA – LÓGICA E MATEMÁTICA – RESUMO 1 DE 4
PROFESSORA KARINE WALDRICH
Boa noite, concurseiros!!
Semana passada fiz um Periscope (me segue lá!! @karinewaldrich) sobre o
ICMS-MA (concurso da Secretaria da Fazenda do Maranhão). No bate-papo que
rolou lá falei sobre o que eu acho relevante estudar para a prova, na parte de
Lógica e Matemática.
Isso mesmo! Eu, professora de Raciocínio Lógico aqui do Ponto há 6 anos,
falando para você NÃO ESTUDAR alguns assuntos?? Estudar só alguns?
Sim!
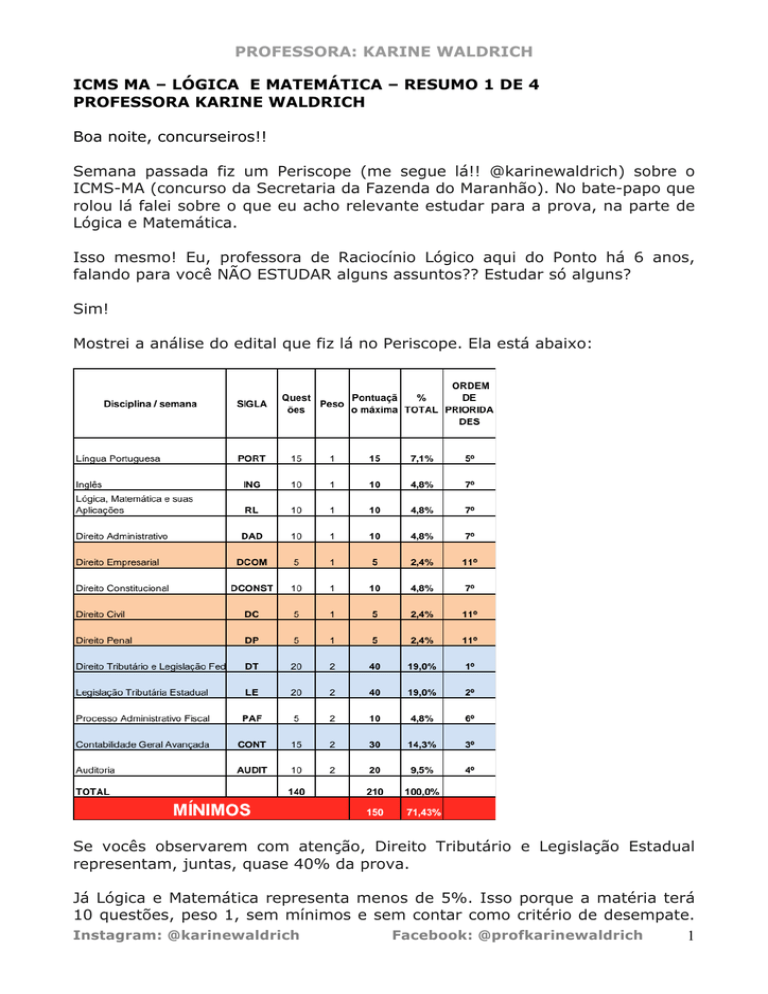
Mostrei a análise do edital que fiz lá no Periscope. Ela está abaixo:
Se vocês observarem com atenção, Direito Tributário e Legislação Estadual
representam, juntas, quase 40% da prova.
Já Lógica e Matemática representa menos de 5%. Isso porque a matéria terá
10 questões, peso 1, sem mínimos e sem contar como critério de desempate.
Instagram: @karinewaldrich
Facebook: @profkarinewaldrich
1
PROFESSORA: KARINE WALDRICH
E o edital é enorme.
Se você for estudar todos os itens do edital vai levar um tempão... Será que
não seria mais inteligente estudar só os assuntos mais fáceis e deixar o tempo
restante para as disciplinas com maior peso na prova (Direito Tributário,
Legislação Estadual e Contabilidade)?
Ora, lógico que você vai estudar só o que vale à pena, afinal você é um
concurseiro que tem FOCO E MALANDRAGEM.
No Periscope também falei sobre quais são esses assuntos que acho que valem
à pena serem estudados, por serem mais fáceis e rápidos de se estudar. São
eles:
⠀
ASSUNTO 1: Lógica: Estruturas Lógicas, Lógica de Argumentação e
Diagramas lógicos. ⠀
ASSUNTO 2: Progressões: Aritmética e Geométrica. Unidades de
Medida. ⠀
ASSUNTO 3: Matemática Comercial e Financeira: Capital e Montante,
Juros simples e Compostos, Taxa de Juros, Desconto. ⠀
ASSUNTO 4: Números e grandezas proporcionais; razão e proporção;
divisão proporcional). Regra de três Simples e Composta,
Porcentagem. ⠀
Bom, então vamos ao que interessa. Vou postar aqui na minha área no site do
Ponto, nesta e nas próximas 3 semanas, RESUMOS COM QUESTÕES
COMENTADAS FCC dos quatro assuntos acima.
Ou seja, se você resolver adotar a minha "tática de guerra" creio que
estudando pelos resumos você já estará bem preparado para fazer a prova de
Lógica e Matemática de maneira INTELIGENTE. ⠀
Os resumos serão postados às sextas-feiras. Ou seja, o cronograma é: ⠀
ASSUNTO
ASSUNTO
ASSUNTO
ASSUNTO
1:
2:
3:
4:
15/07
22/07
29/07
05/08
(HOJE) ⠀
⠀
⠀
⠀
Assim, terminaremos tudo um mês antes da prova, vai dar tempo de revisar
tudo. ⠀
Portanto, hoje veremos um breve resumo do assunto “Estruturas Lógicas,
Lógica de Argumentação e Diagramas Lógicos”, seguido de várias questões
comentadas.
Portanto, vamos começar???
Instagram: @karinewaldrich
Facebook: @profkarinewaldrich
2
PROFESSORA: KARINE WALDRICH
1.1 A Lógica. Proposições
Já vi algumas questões de concurso da FCC com a seguinte definição de
Lógica:
Lógica é o estudo das relações entre afirmações, não da verdade
dessas afirmações. Um argumento é um conjunto de fatos e opiniões
(premissas) que dão suporte a uma conclusão.
Isso não significa que as premissas ou a conclusão sejam
necessariamente verdadeiras; entretanto, a análise dos
argumentos permite que seja testada a nossa habilidade de
pensar logicamente.
(Fonte: Fundação Carlos Chagas)
Assim, em resumo:
1) A Lógica estuda relações entre afirmações, que são chamadas
proposições;
2) As premissas e conclusões não precisam ser necessariamente
verdadeiras;
3) O objetivo é pensar logicamente.
A primeira coisa a aprender quando começamos a estudar o Raciocínio Lógico
é o que são proposições.
Proposição é uma frase, ou uma equação, ou uma expressão, cujo conteúdo
pode ser considerado Verdadeiro ou Falso.
Há dois tipos de proposições: as simples e as compostas.
As proposições simples são afirmações. São frases bem no padrão que
aprendemos em Língua Portuguesa: formadas, no mínimo, por um sujeito e
um verbo.
Exemplo de proposição simples: O Brasil não ganhou a Copa de 2010.
Sabemos que a frase acima é Verdadeira. O Brasil, efetivamente, não ganhou
a Copa de 2010 (quem ganhou foi a Espanha).
Já as proposições compostas são aquelas formadas por duas ou mais
proposições simples. Elas possuem conectivos, ligando uma proposição à
outra.
Por exemplo: A Espanha ganhou a Copa de 2010 e a Holanda ficou em
segundo.
Percebam que, na frase acima, existem 3 proposições:
Instagram: @karinewaldrich
Facebook: @profkarinewaldrich
3
PROFESSORA: KARINE WALDRICH
Proposição 1 (proposição simples): A Espanha ganhou a Copa de 2010
(sabemos que é Verdadeiro).
Proposição 2 (proposição simples): A Holanda ficou em segundo (é
Verdadeiro).
Proposição 3 (proposição composta): A Espanha ganhou a Copa de 2010 e a
Holanda ficou em segundo.
Na Proposição 3, as duas proposições simples estão ligadas pelo conectivo E.
Vamos estudá-lo mais para frente, mas, para uma frase com o conectivo E ser
Verdadeira, as duas proposições simples que a formam devem ser Verdadeiras
também.
Como as duas proposições simples que a formam são realmente Verdadeiras, a
proposição composta também é Verdadeira.
Mas, se disséssemos:
O Brasil ganhou a Copa de 2010 e a Holanda ficou em segundo.
Nesse caso, teríamos uma das proposições simples Verdadeira, e a outra Falsa
(pois o Brasil não ganhou a Copa).
A proposição composta, é, portanto, Falsa, pois, como disse antes, para o
Conectivo E as duas proposições simples devem ser Verdadeiras para a
proposição composta ser Verdadeira.
Podemos utilizar outro conectivo. Se trocarmos o conectivo E pelo Ou, a frase
fica:
O Brasil ganhou a Copa de 2010 ou a Holanda ficou em segundo.
Nesse caso, também temos uma das proposições simples Verdadeira, e a outra
Falsa (pois o Brasil não ganhou a Copa).
No entanto, a proposição composta é Verdadeira. Por que? Porque, para
o conectivo OU, basta que uma das proposições simples sejam Verdadeiras
para a proposição composta ser Verdadeira.
Como a Holanda realmente ficou em segundo na Copa, a proposição composta
com o conectivo Ou é Verdadeira.
Não existem só esses conectivos. Mas a sistemática da coisa é assim. De
acordo com o conectivo usado, as mesmas proposições simples podem
resultar em proposições compostas Verdadeiras ou Falsas.
Instagram: @karinewaldrich
Facebook: @profkarinewaldrich
4
PROFESSORA: KARINE WALDRICH
Voltando a falar sobre as proposições, já sabemos que elas são afirmações de
que podemos extrair um valor lógico (uma “alma”, digamos assim). E este
valor lógico tem que ser sempre Verdadeiro ou Falso.
Dessa forma, não podem ser proposições:
• Sentenças interrogativas: “O que você comeu hoje?” – (não podemos
classificar em verdadeiro ou falso).
• Sentenças imperativas: “Vai lá e depois me conta como foi” – (também
não podemos classificar em verdadeiro ou falso).
• Sentenças exclamativas: “Que legal!!!” (como classificar em verdadeiro
ou falso?).
• Sentenças sem verbo: “Casa azul” (lembrando que “A casa é azul” possui
verbo... e pode ser classificada em verdadeiro ou falso).
• Sentenças que podem mudar de significado. Por exemplo, uma equação
formada apenas por incógnitas.
Agora, vamos ver a fundo cada conectivo. Começaremos pelo conectivo E.
1.2 Conectivo E
Nome: conjunção
Símbolo: ^
O que significa: a proposição composta só será verdadeira se ambas as
proposições simples forem verdadeiras.
Por exemplo:
A Espanha ganhou a Copa de 2010 e a Holanda ficou em segundo.
Se a primeira proposição (A Espanha ganhou a Copa de 2010) estiver correta,
e a segunda (Holanda ficou em segundo) também, a proposição toda (a frase
toda) está correta. Senão, ela está errada.
Ou seja, se V
e V = V.
Da mesma maneira, se uma das proposições estiverem erradas, a proposição
composta estará errada. Portanto:
V
eF=F
Por exemplo:
O Tite é o técnico da Seleção Brasileira e o Rogério Ceni é jogador da Seleção
PS: o Tite é realmente o técnico da seleção brasileira, ou seja, a primeira
proposição está correta. Mas o Rogério Ceni não é jogador da Seleção
Brasileira, então a segunda proposição está errada.
Instagram: @karinewaldrich
Facebook: @profkarinewaldrich
5
PROFESSORA: KARINE WALDRICH
Portanto, o valor lógico (a alma da proposição) é:
V
eF=F
(ou seja, a proposição composta é Falsa)
Mais um exemplo:
O Zagallo é o técnico da Seleção Brasileira e o Neymar é jogador da Seleção.
PS: o Zagallo não é o técnico da seleção brasileira, ou seja, a primeira
proposição está falsa. Mas o Neymar é jogador da Seleção Brasileira, então a
segunda proposição está correta.
Portanto, o valor lógico é:
F
eV=F
(ou seja, a proposição composta é Falsa)
Último exemplo:
O Zagallo é o técnico da Seleção Brasileira e o Rogério Ceni é jogador da
Seleção
PS: o Zagallo não é o técnico da seleção brasileira, ou seja, a primeira
proposição está falsa. E o Rogério Ceni não é jogador da Seleção Brasileira,
então a segunda proposição também está errada.
Portanto, o valor lógico é:
F
eF=F
Assim, em resumo, o conectivo E se comporta da seguinte forma (a tabela
abaixo é conhecida como Tabela-Verdade. Não se preocupem com esse nome
agora, mais a frente falarei mais sobre ela):
CONECTIVO E
eV=V
VeF=F
FeV=F
FeF=F
V
Instagram: @karinewaldrich
Facebook: @profkarinewaldrich
6
PROFESSORA: KARINE WALDRICH
1.3 Conectivo Ou
Nome: disjunção
Símbolo: v
O que significa: Se uma das proposições simples for verdadeira, a
proposição composta já será verdadeira. Dessa forma, ela só será falsa se
ambas as proposições simples forem falsas – em todos os outros casos, a
proposição composta será sempre verdadeira.
Por exemplo:
O Tite é o técnico da Seleção Brasileira
Valor lógico: V
ou o Neymar é jogador da Seleção.
ou V
Como falamos, a proposição composta só será falsa se as duas proposições
estiverem falsas. E, nessa proposição, as duas proposições estão corretas.
Portanto, a proposição composta é Verdadeira.
Ou seja, se V
ou V = V.
Da mesma maneira, se uma das proposições estiver correta, a proposição
composta estará correta. Portanto:
V
ou F = V
Mais um exemplo: O Tite é o técnico da Seleção Brasileira
é jogador da Seleção
ou o Rogério Ceni
Valor lógico: V ou F = V
(ou seja, a proposição composta é Verdadeira)
Terceiro exemplo: O Zagallo é o técnico da Seleção Brasileira ou o Neymar é
jogador da Seleção
Valor lógico: F ou V = V
(ou seja, a proposição composta é Verdadeira)
Último exemplo:
O Zagallo é o técnico da Seleção Brasileira
Seleção
ou o Rogério Ceni é jogador da
Nesse caso, temos duas proposições falsas. Agora sim, a proposição composta
terá valor lógico falso (único caso).
Instagram: @karinewaldrich
Facebook: @profkarinewaldrich
7
PROFESSORA: KARINE WALDRICH
Valor lógico: F ou F = F
(ou seja, a proposição composta é Falsa)
Assim, em resumo, o conectivo OU se comporta da seguinte forma:
CONECTIVO OU
ou V = V
V ou F = V
F ou V = V
F ou F = F
V
1.4 Conectivo Se...Então
Nome: Condicional
Símbolo: à
O que significa: A primeira proposição exprime uma condição para a
segunda. Se a primeira frase for Verdadeira, então a segunda também deverá
ser. Se a primeira frase for Falsa, então a condição não se cumpriu, ou seja,
tanto faz se a segunda frase for Verdadeira ou Falsa, porque a frase toda será
Verdadeira.
Por exemplo:
Se o Tite é o técnico da Seleção Brasileira então o Neymar é jogador da
Seleção.
Valor lógico: Se V então V = V
(ou seja, a proposição composta é Verdadeira)
Mais um exemplo:
Se o Muricy é o técnico da Seleção Brasileira então o Rogério Ceni é jogador
da Seleção.
Valor lógico: Se F então F = V
(ou seja, a proposição composta é Verdadeira)
E
Se o Muricy é o técnico da Seleção Brasileira então o Neymar é jogador da
Seleção.
Valor lógico: Se F então V = V
Instagram: @karinewaldrich
Facebook: @profkarinewaldrich
8
PROFESSORA: KARINE WALDRICH
(ou seja, a proposição composta é Verdadeira)
Reparem que, se a primeira proposição for falsa, a sentença será
sempre verdadeira. Afinal, se o Muricy for o técnico, então o Rogério
Ceni pode ser jogador e o Neymar também. Gravem isso: se a primeia
proposição do Se...então é falsa, a sentença é como um todo é
verdadeira.
Último exemplo:
Se o Tite é o técnico da Seleção Brasileira então o Rogério Ceni é jogador da
Seleção.
Valor lógico: Se V então F = F
(ou seja, a proposição composta é Falsa)
Esse é o caso mais importante, e é dele que vocês vão lembrar toda vez que
fizerem uma questão sobre o assunto.
A sentença composta Se...então só é falsa se a primeira proposição for
verdadeira e a segunda é falsa.
Ou seja, para uma sentença composta, cuja primeira proposição é
verdadeira,
ser
verdadeira,
a
segunda
proposição
deve
NECESSARIAMENTE ser verdadeira também.
Da mesma forma, se a segunda proposição for falsa, a primeira
proposição deverá ser falsa também.
Resumindo, a situação Se V então F é PROIBIDA.
Assim, em resumo, a estrutura Se...então se comporta da seguinte forma:
ESTRUTURA SE...ENTÃO
Se V então V = V
Se V então F = F
Se F então V = V
Se F então F = V
1.5 Conectivo Se e somente se
Nome: bicondicional
Símbolo: ↔
Instagram: @karinewaldrich
Facebook: @profkarinewaldrich
9
PROFESSORA: KARINE WALDRICH
O que significa: A primeira proposição simples exprime uma condição para a
segunda, e a segunda também exprime uma condição para a primeira. A frase
só estará correta se ambas as proposições forem Verdadeiras ou forem
Falsas (uma só não vale).
Por exemplo:
O Neymar é jogador da Seleção se e somente se o Tite é o técnico da
Seleção Brasileira
Valor lógico: V se e somente se V = V
(ou seja, a proposição composta é Verdadeira)
Mais um exemplo: O Neymar é jogador da Seleção se e somente se o
Muricy é o técnico da Seleção Brasileira
Valor lógico: V se e somente se F = F
(ou seja, a proposição composta é Falsa)
Terceiro exemplo: O Rogério Ceni é jogador da Seleção se e somente se o
Tite é o técnico da Seleção Brasileira
Valor lógico: F se e somente se V = F
(ou seja, a proposição composta é Falsa)
Último exemplo: O Rogério Ceni é jogador da Seleção se e somente se o
Muricy é o técnico da Seleção Brasileira
Valor lógico: F se e somente se F = V
(ou seja, a proposição composta é Verdadeira)
Assim, em resumo, o conectivo Se e somente se se comporta da seguinte
forma:
CONECTIVO SE E SOMENTE SE
V se e somente se V = V
V se e somente se F = F
F se e somente se V = F
F se e somente se F = V
1.6 Conectivo Ou...Ou
Nome: disjunção exclusiva
Símbolo:
v
Instagram: @karinewaldrich
Facebook: @profkarinewaldrich
10
PROFESSORA: KARINE WALDRICH
O que significa: Ou um, ou outro. A frase só estará correta se uma das
proposições for Verdadeira e a outra for Falsa (as duas não vale). É o
contrário da estrutura Se e somente se, que vimos acima.
Por exemplo:
Ou o Neymar é jogador da Seleção ou o Tite é o técnico da Seleção Brasileira.
Valor lógico: Ou V ou V = F
(ou seja, a proposição composta é Falsa)
Mais um exemplo: Ou O Neymar é jogador da Seleção ou o Muricy é o
técnico da Seleção Brasileira.
Valor lógico: Ou V ou F = V
(ou seja, a proposição composta é Verdadeira)
Terceiro exemplo: Ou o Rogério Ceni é jogador da Seleção Ou o Tite é o
técnico da Seleção Brasileira
Valor lógico: Ou F ou V = V
(ou seja, a proposição composta é Verdadeira)
Último exemplo: Ou O Rogério Ceni é jogador da Seleção Ou o Muricy é o
técnico da Seleção Brasileira
Valor lógico: Ou F Ou F = F
(ou seja, a proposição composta é Falsa)
Assim, em resumo, o conectivo Ou...Ou se se comporta da seguinte forma:
CONECTIVO OU...OU
Ou V ou V = F
Ou V ou F = V
Ou F ou V = V
Ou F Ou F = F
1.7 Apelidos dos Conectivos
Às vezes, as questões de concursos criam outros nomes para as estruturas que
vimos (os conectivos).
Por exemplo, ao invés de usar Se A, então B, ela usa Quando A, B.
É a mesma coisa, basta trocar pelo Se...então que já conhecemos.
Instagram: @karinewaldrich
Facebook: @profkarinewaldrich
11
PROFESSORA: KARINE WALDRICH
Sintetizei na tabela abaixo os apelidos que já vi serem utilizados em provas.
Primeiramente, vamos ver os apelidos do Se...então.
APELIDOS DA ESTRUTURA SE...ENTÃO
EXEMPLO DE
EQUIVALENTE
APELIDO
PROPOSIÇÃO
COM APELIDO
UTILIZADO
Se o Tite é o
técnico da
Se o Tite é o técnico da
Seleção
Seleção Brasileira então o
Se... (sem o
Brasileira, o
Neymar é jogador da
“então”)
Neymar é
Seleção
jogador da
Seleção
O Neymar é
Se o Tite é o técnico da
jogador da
Seleção Brasileira então o
Seleção, se o
...se (invertido e
Neymar é jogador da
Tite é o técnico
sem o “então”)
Seleção
da Seleção
Brasileira
Quando o Tite
é o técnico da
Se o Tite é o técnico da
Seleção
Seleção Brasileira então o
Brasileira, o
Quando...
Neymar é jogador da
Neymar é
Seleção
jogador da
Seleção
O Tite ser o
técnico da
Se o Tite é o técnico da
Seleção
Seleção Brasileira então o
Brasileira
...implica...
Neymar é jogador da
implica o
Seleção
Neymar ir à
Copa
O Tite ser o
técnico da
Se o Tite é o técnico da
Seleção
Seleção Brasileira então o
Brasileira é
...condição
Neymar é jogador da
condição
suficiente...
Seleção
suficiente para
o Neymar ir à
Copa
Instagram: @karinewaldrich
Facebook: @profkarinewaldrich
12
PROFESSORA: KARINE WALDRICH
Se o Tite é o técnico da
Seleção Brasileira então o
Neymar é jogador da
Seleção
O Tite é o técnico da
Seleção Brasileira se e
somente se o Neymar é
jogador da Seleção
Se o Tite é o técnico da
Seleção Brasileira então o
Neymar é jogador da
Seleção
Se o Tite é o técnico da
Seleção Brasileira então o
Neymar é jogador da
Seleção
Se o Tite é o técnico da
Seleção Brasileira então o
Neymar é jogador da
Seleção
Instagram: @karinewaldrich
O Neymar ir à
Copa é
condição
necessária
...condição
para o Tite ser
necessária...
o técnico da
Seleção
Brasileira.
O Neymar ir à
Copa é
condição
necessária e
...condição
suficiente
necessária e
para o Tite ser
suficiente...
o técnico da
Seleção
Brasileira.
Somente o
Neymar é
...somente...
jogador da
se... (Somente
Seleção se Tite
no início da
é o técnico da
frase)
Seleção
Brasileira
O Tite é o
técnico da
Seleção
...somente se...
Brasileira
(não tem o “se”
somente se o
antes”)
Neymar é
jogador da
Seleção
Toda vez que o
Tite é o técnico
da Seleção
Brasileira o
Neymar é
jogador da
Seleção
Sempre/Toda/
Toda vez que...
Sempre que o
Tite é o técnico
da Seleção
Brasileira o
Neymar é
jogador da
Seleção
Facebook: @profkarinewaldrich
13
PROFESSORA: KARINE WALDRICH
Pintei a linha que fala do “Se” invertido e do “Condição Necessária” para
vocês verem que esses são os únicos casos em que é necessário inverter a
proposição composta. Nos outros, é só trocar o apelido pelo Se...então, sem
inverter.
Da tabela acima, o caso mais cobrado em concurso é, com certeza, o caso da
Condição Suficiente e da Condição Necessária.
Para facilitar a memorização disso, criei um macete, que uso desde os tempos
de faculdade. É o Macete do Sol e Nuvem. Não riam, porque na hora da prova
tenho certeza que vocês vão acertar a questão por causa dele:
MACETE DO SOL E NUVEM
Basta substituir pelo
Condição
Suficiente
Condição
Necessária
Dia de
Se...então
Sol
Dia de
Nuvem
Deve-se inverter as
proposições primeiro, para
depois substituir pelo
Se...então
Esse macete serve para lembrar que, se a frase possui Sol (condição
suficiente) basta substituir diretamente por Se...então.
No entanto, se for dia de Nuvem (condição necessária), não é tão simples,
deve-se inverter as proposições, para depois substituir pelo Se...então.
A estrutura Se e somente se também possui um apelido:
APELIDO DA ESTRUTURA SE E SOMENTE SE
EXEMPLO DE
EQUIVALENTE
APELIDO
PROPOSIÇÃO
COM APELIDO
UTILIZADO
Instagram: @karinewaldrich
Facebook: @profkarinewaldrich
14
PROFESSORA: KARINE WALDRICH
O Neymar é jogador da
Seleção se e somente se
o Tite é o técnico da
Seleção Brasileira
O Tite ser o
técnico da
Seleção
Brasileira é
condição
necessária e
suficiente para
o Neymar ir à
Copa
Condição
necessária e
suficiente
Agora falaremos de um assunto importante, os equivalentes lógicos.
1.8 Proposições Equivalentes
Duas proposições são equivalentes quando querem dizer a mesma coisa. Para
ficar mais claro, vamos resolver utilizando o conceito das tabelas-verdade.
Tabela-verdade é um nome difícil para aqueles esquemas que vimos em cada
Estrutura, do tipo:
ESTRUTURA SE...ENTÃO
Se V então V = V
Se V então F = F
Se F então V = V
Se F então F = V
Essa é a tabela-verdade da Estrutura Se...então. Ela lista todas as
possibilidades para as proposições com a estrutura.
Sabendo isso, devemos deixar claro que Equivalentes
proposições em que as tabelas-verdade são iguais.
Lógicos
são
Vamos ver com mais detalhes nas questões. Resumidamente, vou sintetizar as
proposições equivalentes na tabela abaixo:
PROPOSIÇÃO
CONDICIONAL
Se...então
pàq
EQUIVALENTES LÓGICOS
PROPOSIÇÃO
EXEMPLO
EQUIVALENTE
~q → ~p
Se o Tite é o
técnico da
(É a condicional Seleção Brasileira
com os termos
então o Neymar
invertidos e
é jogador da
negados)
Seleção
Instagram: @karinewaldrich
RESULTADO
Se o Neymar não é
jogador da Seleção
então o Tite não é o
técnico da Seleção
Brasileira.
Facebook: @profkarinewaldrich
15
PROFESSORA: KARINE WALDRICH
O Tite não é o
técnico da Seleção
Brasileira ou o
Neymar é jogador da
Seleção
~p v q
q v ~p
(É a disjunção
com o primeiro
termo da
condicional
negado)
BICONDICION
AL
Se somente se
p
↔q
DISJUNÇÃO
EXCLUSIVA
Ou...Ou...
pvq
(p à q) ^ (q à p)
(É a condicional
de ida E a
condicional de
volta)
p à ~q
~p à q
(É a
bicondicional
com o um dos
termos negados)
O Tite é o técnico
da Seleção
Brasileira se e
somente se o
Neymar é jogador
da Seleção
Ou o Tite é o
técnico da
Seleção Brasileira
ou o Neymar é
jogador da
Seleção
O Neymar é jogador
da Seleção ou o Tite
não é o técnico da
Seleção Brasileira.
Se o Tite é o técnico
da Seleção Brasileira
então o Neymar é
jogador da Seleção E
Se o Neymar é
jogador da Seleção
então o Tite é o
técnico da Seleção
Brasileira
O Tite é o técnico da
Seleção Brasileira se
e somente se o
Neymar não é
jogador da Seleção
O Tite não é o
técnico da Seleção
Brasileira se e
somente se o
Neymar é jogador da
Seleção
1.9 Negação de proposições
Negar uma proposição é inverter o seu sentido. Falando em termos de tabelaverdade, uma proposição é negação de outra quando suas tabelas-verdade
forem opostas (o que é Verdadeiro em uma, é Falso em outra, e vice-versa).
Sintetizei as negações na tabela abaixo. Veremos como funciona na prática
durante os exercícios comentados.
NEGAÇÃO DE PROPOSIÇÕES COMPOSTAS
NEGAÇÃO
EXEMPLO
Instagram: @karinewaldrich
COMO FAZER
(Passo-a-passo)
RESULTADO
Facebook: @profkarinewaldrich
16
PROFESSORA: KARINE WALDRICH
Negação de
conjunção
=
~(p ^ q)
Negação de
disjunção
=
~(p v q)
Negação de
disjunção
exclusiva
=
~(p v q)
Negação de
condicional
=
~(p à q)
Negação de (O
Tite é o técnico da
Seleção Brasileira
e o Neymar é
jogador da
Seleção)
OBS: existem
duas maneiras de
se negar uma
conjunção. Na
primeira, forma-se
uma disjunção (p
OU q). Na
segunda, forma-se
uma condicional
(se p, então q).
Negação de (O
Tite é o técnico da
Seleção Brasileira
ou o Neymar é
jogador da
Seleção)
Para se formar uma
disjunção:
1º: Negar a primeira
(p)
2º: Negar a segunda
(q)
3: Trocar o e por ou
Para se formar uma
condicional:
1º: Manter a primeira
(p)
2º: Negar a segunda
(q)
3: Trocar o e por à
1º: Negar a primeira
(p)
2º: Negar a segunda
(q)
3: Trocar o ou por e
1º: Substituir o v por
Negação de (Ou o
Tite é o técnico da
Seleção Brasileira
ou o Neymar é
jogador da
Seleção)
Negação de (Se o
Tite é o técnico da
Seleção Brasileira
então o Neymar é
jogador da
Seleção)
Instagram: @karinewaldrich
↔
OBS: vocês se lembram
que já vimos isso,
quando falamos sobre o
conectivo Se e somente
se?
1º: Manter a primeira
(p)
2º: Negar a segunda
(q)
3: Trocar o à por e
O Tite não é o
técnico da Seleção
Brasileira ou o
Neymar não é
jogador da Seleção
=
~p v ~q
Se o Tite é o técnico
da Seleção Brasileira
então o Neymar não
é jogador da Seleção
=
p
à ~q
O Tite não é o
técnico da Seleção
Brasileira ou o
Neymar não é
jogador da Seleção
=
~p ^ ~q
O Tite é o técnico da
Seleção Brasileira se
e somente se o
Neymar é jogador da
Seleção
=
p↔q
O Tite é o técnico da
Seleção Brasileira e
o Neymar não é
jogador da Seleção
=
Facebook: @profkarinewaldrich
17
PROFESSORA: KARINE WALDRICH
Negação de
bicondicion
al
=
~(p
↔ q)
Negação de (O
Tite é o técnico da
Seleção Brasileira
se e somente se
o Neymar é
jogador da
Seleção)
1º: Substituir o
v
↔ por
OBS: reparem que
estamos fazendo o
inverso do que fizemos
acima (na negação da
disjunção exclusiva)
p ^ ~q
Ou o Tite é o técnico
da Seleção Brasileira
ou o Neymar é
jogador da Seleção
=
pvq
1.10 Estruturas Todo, Algum e Nenhum – Diagramas Lógicos
Diagramas Lógicos são mecanismos utilizados para expressar proposições que
alguns matemáticos chamam de “categóricas”: Todo, algum, nenhum.
Quando dizemos, por exemplo: todo brasileiro é uma pessoa inteligente.
Podemos traduzir a ideia dessa frase em um diagrama:
Pessoa inteligente
Brasileiro
Vamos ver todas as possibilidades para a frase acima:
Brasileiro
Pessoa
inteligente
Todo brasileiro é uma
pessoa inteligente
V
V
V
F
Verdadeiro, pois se ele for
brasileiro, será uma pessoa
inteligente (dentro da área
amarela do diagrama)
Falso, pois não existe a
possibilidade de ser
brasileiro e não ser uma
pessoa inteligente
Instagram: @karinewaldrich
Facebook: @profkarinewaldrich
18
PROFESSORA: KARINE WALDRICH
F
V
F
F
Verdadeiro, pois ele pode ser
uma pessoa inteligente e não
ser brasileiro (estar na área
laranja do diagrama)
Verdadeiro, pois ele pode
não ser brasileiro e, assim,
não ser uma pessoa
inteligente (estar fora do
diagrama, na área em cinza)
Portanto, a única possibilidade de a frase ser falsa é no caso em que o sujeito
é brasileiro e não é uma pessoa inteligente, pois essa possibilidade não existe.
A tabela acima é igual à tabela-verdade da estrutura Se...então. Podemos
dizer, então, que Todo brasileiro é uma pessoa inteligente e Se é
brasileiro, então é uma pessoa inteligente são equivalentes.
Passando para outra estrutura: o algum. Podemos dizer: Alguns brasileiros
são pessoas inteligentes. Isso pode ser representado através do diagrama
abaixo:
Pessoa
inteligente
Brasileiro
Agora, todas as possibilidades são possíveis. O sujeito pode ser brasileiro e ser
ou não uma pessoa inteligente, assim como pode ser inteligente e ser ou não
brasileiro.
Portanto, é importante frisar que, neste caso, alguns brasileiros são
pessoas inteligentes e algumas pessoas inteligentes são brasileiras são
frases equivalentes:
Instagram: @karinewaldrich
Facebook: @profkarinewaldrich
19
PROFESSORA: KARINE WALDRICH
Pessoa
=
Brasileiro
inteligente
Pessoa
Brasileiro
inteligente
Passemos para o nenhum. Podemos dizer: nenhum brasileiro é uma pessoa
inteligente. Isso é representado através do diagrama abaixo:
Pessoa
inteligente
Brasileiro
Dizer nenhum brasileiro é uma pessoa inteligente e nenhuma pessoa
inteligente é brasileira são expressões equivalentes, como podemos ver
pelo diagrama acima.
Vamos colocar todas as possibilidades de nenhum brasileiro é uma pessoa
inteligente numa tabela:
Brasileiro
Pessoa
inteligente
Nenhum brasileiro é uma
pessoa inteligente
V
V
V
F
Falso, pois se ele for
brasileiro, não será uma
pessoa inteligente
Verdadeiro, pois se ele for
brasileiro, não será uma
Instagram: @karinewaldrich
Facebook: @profkarinewaldrich
20
PROFESSORA: KARINE WALDRICH
F
V
F
F
pessoa inteligente
Falso, pois se ele não for
brasileiro, pode ou não ser
uma pessoa inteligente (não
estar dentro do diagrama
amarelo não significa
necessariamente estar
dentro do diagrama laranja.
Pode estar na área em cinza)
Falso, pois a pessoa pode
não ser brasileira e ser
inteligente
Percebam que a tabela-verdade acima é igual à tabela-verdade da estrutura
Se...~então. Vou fazer a Se...~então para vocês verem:
Brasileiro
Pessoa
inteligente
V
V
Pessoa
nãointeligente
F
V
F
V
F
V
F
F
F
V
Se é brasileiro, então não é uma pessoa
inteligente
Falso, pois se ele for brasileiro, é
verdadeiro dizer que não será uma
pessoa inteligente, e não falso
Verdadeiro, pois se ele for brasileiro,
não será uma pessoa inteligente
Falso, pois se ele não for brasileiro, pode
ou não ser uma pessoa inteligente (é
falso dizer que, só por não ser brasileiro,
será inteligente)
Falso, pois a pessoa pode não ser
brasileira e ser inteligente
Portanto, são equivalentes as frases nenhum brasileiro é inteligente e se é
brasileiro, então não é inteligente.
Vamos, ainda, falar sobre a negação do Todo, Algum e Nenhum.
Primeiramente, o Todo. Qual a negação de Todo A é
B
A
Instagram: @karinewaldrich
Facebook: @profkarinewaldrich
21
PROFESSORA: KARINE WALDRICH
Podemos pensar que seria Nenhum A é B:
B
A
Mas vejam que não, necessariamente. Se houver algum A que não for B, a
frase Todo A é B já está falsa. Portanto, basta ter a certeza de que há
Algum A não é B.
Assim, a negação de Todo A é B é Algum A não é B.
~ (Todo A é B) = Algum A não é B
Por exemplo: Todo múltiplo de 100 é divisível por 5. A negação é Algum
múltiplo de 100 não é divisível por 5.
Agora passamos à negação do Algum. Algum A é B:
B
A
O Algum indica que pelo menos 1 A é B. A negação disso é dizer que nenhum
A é B. Como a palavra diz, nem-hum (nem um). São totalmente separados:
B
Instagram: @karinewaldrich
A
Facebook: @profkarinewaldrich
22
PROFESSORA: KARINE WALDRICH
~ (Algum A é B) = Nenhum A é B
Já a negação do Nenhum é o contrário do que vimos acima. Negar que
Nenhum A é B é dizer que Algum A é B.
~ (Nenhum A é B) = Algum A é B
Instagram: @karinewaldrich
Facebook: @profkarinewaldrich
23
PROFESSORA: KARINE WALDRICH
2. Exercícios Comentados
2016/FCC/ TRF - 3ª REGIÃO/Analista Judiciário - Área Administrativa
Considere verdadeiras as afirmações abaixo.
I. Ou Bruno é médico, ou Carlos não é engenheiro.
II. Se Durval é administrador, então Eliane não é secretária.
III. Se Bruno é médico, então Eliane é secretária.
IV. Carlos é engenheiro.
A partir dessas afirmações, pode-se concluir corretamente que
a) Eliane não é secretária e Durval não é administrador.
b) Bruno não é médico ou Durval é administrador.
c) se Eliane não é secretária, então Bruno não é médico.
d) Carlos é engenheiro e Eliane não é secretária.
e) se Carlos é engenheiro, então Eliane não é secretária.
Esse tipo de questão é clássica na FCC e tem um modus operandi bem padrão.
Vou pedir para vocês prestarem bastante atenção pois é bem capaz de uma
questão semelhante cair na prova da SEFAZ MA!!!
Antes de qualquer coisa vou definir com vocês que quando eu falar em
AFIRMAÇÃO, estou me referindo a uma das 4 afirmações do enunciado (I, II,
III ou IV).
Já quando eu falar em PARTE, estarei me referindo às partes de dentro da
AFIRMAÇÃO. POR EXEMPLO: A AFIRMAÇÃO I tem duas PARTES: "Bruno é
médico” e "Carlos não é engenheiro".
CERTINHO???
DITO ISSO, A primeira coisa a se fazer é atentar para SE HÁ OU NÃO UMA
AFIRMAÇÃO que NÃO POSSUI PROPOSIÇÃO. Na FCC, se houver uma afirmação
sem proposição, ela será a última das 4.
Repare que a afirmação IV não possui nenhuma proposição. Ela apenas diz que
Carlos é engenheiro, sem E, OU, SE…ENTÃO… nada.
Então, “Carlos é engenheiro” é um FATO, você não precisa tentar descobrir se
Carlos é engenheiro porque ele É. SIMPLES ASSIM kkk
A partir dela, você descobrirá o valor lógico das demais. Não vou falar muito,
vou direto para a resolução, aí vou explicando durante, ok???
(OBS: vou fazer uma outra questão para quando a FCC não der essa afirmação
sem proposição de bandeja, ok? Mais para frente).
Instagram: @karinewaldrich
Facebook: @profkarinewaldrich
24
PROFESSORA: KARINE WALDRICH
Bom, voltando, temos que Carlos é engenheiro, e TODAS AS PARTES QUE
DISSEREM ISSO SERÃO VERDADEIRAS. JÁ TODAS AS PARTES QUE DISSEREM
O CONTRÁRIO SERÃO FALSAS.
Tem alguma PARTE ali que diga isso ou o contrário? Sim, reparem que na
afirmação I é dito que Carlos não é engenheiro.
Mas nós já sabemos que ele É, portanto essa PARTE é Falsa. REPAREM QUE
UMA “PARTE" PODE SER FALSA, MAS A AFIRMAÇÃO INTEIRA NUNCA, OK?????
Vamos marcar em cima dela com um F (é EXATAMENTE ASSIM QUE VOCÊS
VÃO FAZER NA HORA DA PROVA OK???? MARCAR DE LÁPIS EM CIMA DO
ENUNCIADO).
Portanto, temos:
F
I. Ou Bruno é médico, ou Carlos não é engenheiro.
II. Se Durval é administrador, então Eliane não é secretária.
III. Se Bruno é médico, então Eliane é secretária.
IV. Carlos é engenheiro.
Agora vem o PULO DO GATO, que vocês vão levar para a vida e que vale para
toda e qualquer questão de lógica que aparecer. COMO JÁ DISSE, ESSA PARTE
É FALSA, MAS A AFIRMAÇÃO TODA É VERDADEIRA. SEMPRE. POIS O
ENUNCIADO DISSE QUE TODAS AS AFIRMAÇÕES ERAM VERDADEIRAS.
OK???????????????
Então, o que é necessário para que a afirmação I seja Verdadeira, sendo que a
segunda parte dela é Falsa?
Bom, pelo que vemos ali, é uma afirmação com o conectivo OU…OU. O nome
desse conectivo é OU exclusivo. Pelo Memorex, vemos que quando a afirmação
tem o OU sozinho, para ela ser Verdadeira no mínimo UMA DAS PARTES (OU
AS DUAS) devem ser Verdadeiras. Já no OU…OU (o OU exclusivo), para a
AFIRMAÇÃO ser Verdadeira APENAS UMA das PARTES pode ser Verdadeira.
Assim, como vimos que a segunda parte dela é Falsa (afinal Carlos é
engenheiro), a primeira parte deve ser obrigatoriamente Verdadeira. Ou seja,
Bruno deve ser médico. Marque com um V em cima disso:
V
F
I. Ou Bruno é médico, ou Carlos não é engenheiro.
II. Se Durval é administrador, então Eliane não é secretária.
III. Se Bruno é médico, então Eliane é secretária.
IV. Carlos é engenheiro.
De agora em diante, o que acontece é uma escadinha. Ter descoberto que
Bruno é médico vai levar você a saber o valor lógico de outra parte, que vai
Instagram: @karinewaldrich
Facebook: @profkarinewaldrich
25
PROFESSORA: KARINE WALDRICH
levar a outra, assim por diante.
Para isso, basta procurar a outra PARTE que fale do Bruno. Qual é? Na
afirmação III. Vejam que a primeira parte diz que Bruno é médico. Isso é
Verdadeiro? Sim, por isso colocamos um V em cima (se fosse Falso
colocaríamos um F).
V
F
I. Ou Bruno é médico, ou Carlos não é engenheiro.
II. Se Durval é administrador, então Eliane não é secretária.
V
III. Se Bruno é médico, então Eliane é secretária.
IV. Carlos é engenheiro.
No entanto, agora, ao invés do OU temos o SE…ENTÃO. No Se…então, a
afirmação só vai ser Falsa no caso SE V ENTÃO F. Em todos os outros casos ela
é Verdadeira.
Podemos ter afirmações Falsas???? Não. Então, como a primeira parte é
Verdadeira, a segunda não vai poder ser Falsa, pois senão temos o caso SE V
ENTÃO F, que é Falso (nas aulas chamamos o Se V Então F de CASO
PROIBIDO, pois ele NUNCA PODE ACONTECER. NUNCA NUNQUINHA).
Como SE V ENTÃO F é o caso proibido e nunca pode acontecer, então só
podemos ter SE V ENTÃO V. Assim quando a primeira parte de uma afirmação
com Se…Então for V, a segunda parte SEMPRE VAI SER V.
Assim, descobrimos que Eliane é secretária.
V
F
I. Ou Bruno é médico, ou Carlos não é engenheiro.
II. Se Durval é administrador, então Eliane não é secretária.
V
V
III. Se Bruno é médico, então Eliane é secretária.
IV. Carlos é engenheiro.
Agora fazemos O MESMO de antes, procurando alguma parte que fale da
Eliana nas afirmações. Na afirmação II é dito que Eliana não é secretária. Isso
é FALSO, como vimos:
V
F
I. Ou Bruno é médico, ou Carlos não é engenheiro.
F
II. Se Durval é administrador, então Eliane não é secretária.
V
V
III. Se Bruno é médico, então Eliane é secretária.
IV. Carlos é engenheiro.
Aqui ocorre O MESMO caso de antes. Se a primeira parte da afirmação II for V
Instagram: @karinewaldrich
Facebook: @profkarinewaldrich
26
PROFESSORA: KARINE WALDRICH
teremos o CASO PROIBIDO SE V ENTÃO F. Então, a primeira parte deverá ser
F:
V
F
I. Ou Bruno é médico, ou Carlos não é engenheiro.
F
F
II. Se Durval é administrador, então Eliane não é secretária.
V
V
III. Se Bruno é médico, então Eliane é secretária.
IV. Carlos é engenheiro.
Assim, atingimos nosso objetivo, pois descobrimos o valor lógico de TODAS AS
PARTES (Carlos é engenheiro é V também, certo?).
Então, concluímos que:
-
Carlos é engenheiro (isso não concluímos, foi a própria questão que falou);
Bruno é médico;
Durval não é administrador;
Eliane é secretária.
Sabendo disso, passamos à análise das alternativas:
a) Eliane não é secretária e Durval não é administrador.
Para uma AFIRMAÇÃO com o E ser Verdadeira, ambas as frases devem ser
Verdadeiras. Mas a primeira parte está errada, porque Eliane é secretária.
Alternativa errada.
b) Bruno não é médico ou Durval é administrador.
Bruno é médico e Durval não é administrador. Ou seja, ambas as partes são
Falsas. Para uma afirmação com o OU ser Verdadeira, ao menos uma parte
deve ser Verdadeira. Alternativa errada.
c) se Eliane não é secretária, então Bruno não é médico.
Quando há o Se…Então, a afirmação só será Falsa quando Se V então F.
“Se Eliane não é secretária” é “Se F”, pois Eliane é secretária.
˜então Bruno não é médico” é “então F”, pois Bruno é médico.
Assim, temos “Se F então F”, que é sempre Verdadeiro.
Alternativa correta.
d) Carlos é engenheiro e Eliane não é secretária.
Instagram: @karinewaldrich
Facebook: @profkarinewaldrich
27
PROFESSORA: KARINE WALDRICH
Carlos é engenheiro, mas Eliane é secretária, e quando há o E ambas as partes
devem estar corretas. Alternativa errada.
e) se Carlos é engenheiro, então Eliane não é secretária.
Temos Se V então F, que é sempre Falso (caso proibido).
Resposta: Letra C.
2015/FCC/DPE-RR/Auxiliar Administrativo
Considere as afirmações:
Se Janete sair mais cedo, então Clara ficará trabalhando até mais
tarde.
Dalva não foi trabalhar.
A partir das afirmações é correto concluir que
a) Clara ficou trabalhando até mais tarde.
b) Janete não foi trabalhar.
c) Dalva foi trabalhar.
d) Janete não saiu mais cedo.
e) Clara não foi trabalhar.
Olha ela ali genteeee… A afirmação sem proposição!!!! “Dalva não foi
trabalhar”. A partir dela resolvemos as outras.
A segunda afirmação diz: Se Dalva não for trabalhar, então Janete sairá mais
cedo. Então temos SE V (pois Dalva não foi trabalhar). Hmmmmm, “Janete
sairá mais cedo” pode ser FALSO?? Não, pois se for Falso teremos o caso
proibido Se V então F. Assim, "Janete sairá mais cedo” deve ser
obrigatoriamente Verdadeiro.
O MESMO OCORRE NA PRIMEIRA AFIRMAÇÃO, "Se Janete sair mais cedo,
então Clara ficará trabalhando até mais tarde.”, POIS TEMOS “SE V”. Assim,
"Clara ficará trabalhando até mais tarde” deve ser V também.
Portanto, sabemos que:
(A) Dalva não foi trabalhar.
- Janete sairá mais cedo
(A) Clara ficará trabalhando até mais tarde
A única alternativa que tem a ver com as infos acima é a letra A.
Resposta: letra A.
Instagram: @karinewaldrich
Facebook: @profkarinewaldrich
28
PROFESSORA: KARINE WALDRICH
2016/FCC/TRF - 3ª REGIÃO/Analista Judiciário - Área Administrativa
Considere, abaixo, as afirmações e o valor lógico atribuído a cada uma
delas entre parênteses.
− Ou Júlio é pintor, ou Bruno não é cozinheiro (afirmação FALSA).
− Se Carlos é marceneiro, então Júlio não é pintor (afirmação FALSA).
− Bruno é cozinheiro ou Antônio não é pedreiro (afirmação
VERDADEIRA).
A partir dessas afirmações,
a) Júlio não é pintor e Bruno não é cozinheiro.
b) Antônio é pedreiro ou Bruno é cozinheiro.
c) Carlos é marceneiro e Antônio não é pedreiro.
d) Júlio é pintor e Carlos não é marceneiro.
e) Antônio é pedreiro ou Júlio não é pintor.
RESOLUÇÃO CORRETA ABAIXO:
Questão tipo a anterior só que mais dificinha porque o enunciado não dá
nenhuma frase pronta de presente.
Então, o melhor a se fazer nessas horas é CHUTAR. Mas claro que não é um
chute assim no vazio, meu nome é WALDRICH, sou alemã e chuto bem pacas
(7 x 1, lembram-se?? vraaaa).
Ora, a FCC pensa que é esperta mas ela sempre deixa um furo. SEMPRE. E
vejam o furo nessa questão: ela diz que a segunda afirmação é FALSA. E é um
SE…ENTÃO!!!!!!!!
Sabemos que o Se…Então só é Falso quando SE V ENTÃO F.
Assim, "Se Carlos é marceneiro, então Júlio não é pintor” só pode ser SE V
ENTÃO F. Assim, sabemos que, OBRIGATORIAMENTE:
(A)Carlos é marceneiro;
(B) Júlio é pintor.
Onde mais fala de Carlos ou Julio? Na primeira afirmação, ali diz que "Ou Júlio
é pintor, ou Bruno não é cozinheiro”.
Como é Ou…Ou, sabemos que para ser Verdadeiro obrigatoriamente uma das
partes deve ser Verdadeira e a outra Falsa (nunca as duas juntas).
Mas O ENUNCIADO DIZ que a afirmação é Falsa, ou seja, para ser Falsa
ambas devem ser Verdadeiras ou ambas devem ser Falsas.
Oras, Júlio é pintor. Afirmação Verdadeira. Portanto “Bruno não é cozinheiro”
Instagram: @karinewaldrich
Facebook: @profkarinewaldrich
29
PROFESSORA: KARINE WALDRICH
deve ser obrigatoriamente Verdadeiro. Assim, Bruno não é cozinheiro.
Passemos para a última afirmação, que diz que Bruno é cozinheiro. O
conectivo ali é o OU (só UM OU), então para a afirmação ser Verdadeira pode
tanto haver apenas uma parte Verdadeira como as duas. Assim, como Bruno
não é cozinheiro, “Antônio não é pedreiro” deve ser Verdadeiro.
Passemos à análise das alternativas.
a) Júlio não é pintor e Bruno não é cozinheiro.
Júlio é pintor. Errado.
b) Antônio é pedreiro ou Bruno é cozinheiro.
Antônio não é pedreiro. Bruno não é cozinheiro. Errado.
c) Carlos é marceneiro e Antônio não é pedreiro.
Carlos é marceneiro, e Antônio não é pedreiro. Verdadeiro.
Alternativa correta.
d) Júlio é pintor e Carlos não é marceneiro.
Carlos é marceneiro. Errada.
e) Antônio é pedreiro ou Júlio não é pintor.
Antônio não é pedreiro. Júlio é pintor. Falso.
Resposta: letra C.
RESOLUÇÃO ANTERIOR (ERRADA)
Questão tipo a anterior só que mais dificinha porque o enunciado não dá
nenhuma frase pronta de presente.
Então, o melhor a se fazer nessas horas é CHUTAR. Mas claro que não é um
chute assim no vazio, meu nome é WALDRICH, sou alemã e chuto bem pacas
(7 x 1, lembram-se?? vraaaa).
Ora, a FCC pensa que é esperta mas ela sempre deixa um furo. SEMPRE. E
vejam o furo nessa questão: ela diz que a segunda afirmação é FALSA. E é um
SE…ENTÃO!!!!!!!!
Sabemos que o Se…Então só é Falso quando SE V ENTÃO F.
Assim, "Se Carlos é marceneiro, então Júlio não é pintor” só pode ser SE V
Instagram: @karinewaldrich
Facebook: @profkarinewaldrich
30
PROFESSORA: KARINE WALDRICH
ENTÃO F. Assim, sabemos que, OBRIGATORIAMENTE:
(C) Carlos é marceneiro;
(D)Júlio é pintor.
Onde mais fala de Carlos ou Julio? Na primeira afirmação, ali diz que "Ou Júlio
é pintor, ou Bruno não é cozinheiro”. Como é Ou…Ou, sabemos que para ser
Verdadeiro obrigatoriamente uma das partes deve ser Verdadeira e a outra
Falsa (nunca as duas juntas).
Oras, Júlio é pintor. Portanto “Bruno não é cozinheiro” deve ser
obrigatoriamente Falso. Assim, Bruno é cozinheiro.
Passemos para a última afirmação, que diz que Bruno é cozinheiro. O
conectivo ali é o OU (só UM OU), então para a afirmação ser Verdadeira pode
tanto haver apenas uma parte Verdadeira como as duas. Assim, como Bruno é
cozinheiro, “Antônio não é pedreiro” pode ser tanto Verdadeiro como Falso
(não dá para saber).
Passemos à análise das alternativas.
a) Júlio não é pintor e Bruno não é cozinheiro.
Júlio é pintor. Errado.
b) Antônio é pedreiro ou Bruno é cozinheiro.
Não sabemos se Antônio é pedreiro ou não, mas Bruno é cozinheiro sim. Como
há o OU, basta ter uma parte Verdadeira para a afirmação ser Verdadeira.
Alternativa correta.
c) Carlos é marceneiro e Antônio não é pedreiro.
Não sabemos se Antônio não é pedreiro, e como há o E, só estaria certo se
tivéssemos certeza de que "Antônio não é pedreiro” é Verdadeiro. Errada.
d) Júlio é pintor e Carlos não é marceneiro.
Carlos é marceneiro. Errada.
e) Antônio é pedreiro ou Júlio não é pintor.
Júlio é pintor, então a segunda parte está errada com certeza. E não sabemos
se Antônio é pedreiro, então não dá para saber se a primeira parte é
Verdadeira. Para o OU, ao menos uma das partes deve ser Verdadeira, e não
podemos garantir nada por não saber o que se passou com o serumaninho
Antônio.
Instagram: @karinewaldrich
Facebook: @profkarinewaldrich
31
PROFESSORA: KARINE WALDRICH
Resposta: letra B.
2000/FCC/TCE-GO/Téc. Jud.
Uma proposição de uma linguagem é uma expressão de tal linguagem
que pode ser classificada como verdadeira ou falsa. Com base nessa
definição, analise as seguintes expressões:
I. 3 + 8 < 13
II. Que horas são?
III. Existe um número inteiro x tal que 2x > -5.
IV. Os tigres são mamíferos.
V. 36 é divisível por 7.
VI. x +y = 5
É correto afirmar que são proposições APENAS as expressões
(A) I e IV.
(B) I e V.
(C) II, IV e VI.
(D) III, IV e V.
(E) I, III, IV e V.
Essa questão é muito boa pois versa sobre um aspecto bem inicial do estudo
das Estruturas Lógicas: o que é uma proposição?
Como vimos, proposição é uma frase, ou uma equação, ou uma expressão,
cujo conteúdo pode ser considerado Verdadeiro ou Falso.
Sabendo isso, vamos analisar as sentenças da questão?
I. 3 + 8 < 13
3 + 8 sabemos que é 11. A questão afirma ser menor do que 13, ou seja, a
afirmação é verdadeira. Como podemos classificar dessa maneira, a sentença é
proposição.
II.
Que horas são?
Já sabemos que sentenças interrogativas não são proposições.
III. Existe um número inteiro x tal que 2x > -5.
A questão afirma que existe um número x tal que 2x > -5. Ou seja, ela pode
estar verdadeira ou falsa. Nem precisamos resolver a equação para saber se a
sentença é verdadeira ou falsa, pois o simples fato de poder ser classificada de
uma maneira ou de outra já a torna proposição. Ou seja, a sentença é
proposição.
Instagram: @karinewaldrich
Facebook: @profkarinewaldrich
32
PROFESSORA: KARINE WALDRICH
IV.
Os tigres são mamíferos.
Nem precisa lembrar de biologia. Sendo ou não mamíferos (para quem não
lembra, os tigres são sim mamíferos), a sentença pode ser classificada em
verdadeiro ou falso. Ou seja, é proposição.
V. 36 é divisível por 7.
Mais uma vez, nem precisamos resolver a conta proposta para sabermos se a
afirmação é verdadeira ou falsa, para saber que ela pode ser classificada
assim. Ou seja, a afirmação é uma proposição.
VI.
x+y=5
Será que x + y = 5 é verdadeiro ou falso? Depende. Por exemplo, se x = 2 e y
= 3, a afirmação será verdadeira. Já, se x = y = 3, a afirmação será falsa.
Ou seja, não podemos classificar a sentença acima em verdadeiro ou falso,
pois, a cada valor das incógnitas x e y, o valor lógico da sentença muda.
Gravem isso: não existe “depende” em relação a proposições. Elas devem ser
verdadeiras ou falsas, e isso deve ser definido, constante e imutável.
Assim, são proposições as alternativas I, III, IV e V.
Resposta: letra E.
2010/FCC/TCE-SP/AFF
Certo dia, cinco Agentes de um mesmo setor do Tribunal de Contas do
Estado de São Paulo − Amarilis, Benivaldo, Corifeu, Divino e Esmeralda
− foram convocados para uma reunião em que se discutiria a
implantação de um novo serviço de telefonia. Após a realização dessa
reunião, alguns funcionários do setor fizeram os seguintes
comentários:
– “Se Divino participou da reunião, então Esmeralda também
participou”;
– “Se Divino não participou da reunião, então Corifeu participou”;
– “Se Benivaldo ou Corifeu participaram, então Amarílis não
participou”;
– “Esmeralda não participou da reunião”.
Considerando que as afirmações contidas nos quatro comentários
eram verdadeiras, pode-se concluir com certeza que, além de
Esmeralda, não participaram de tal reunião
(A) Amarilis e Benivaldo.
Instagram: @karinewaldrich
Facebook: @profkarinewaldrich
33
PROFESSORA: KARINE WALDRICH
(B) Amarilis e Divino.
(C) Benivaldo e Corifeu.
(D) Benivaldo e Divino.
(E) Corifeu e Divino.
A grande chave para a resolvê-la é perceber que uma das frases é
simplesmente uma afirmação verdadeira (como frisa o enunciado). A frase:
“Esmeralda não participou da reunião” é uma premissa, absolutamente
Verdadeira.
Colocamos um V sobre esta afirmação:
– “Se Divino participou da reunião, então Esmeralda também participou”;
– “Se Divino não participou da reunião, então Corifeu participou”;
– “Se Benivaldo ou Corifeu participaram, então Amarílis não participou”;
V
– “Esmeralda não participou da reunião”.
Analisando as demais proposições, reparamos que a primeira proposição
também fala em Esmeralda, dizendo que ela participou da reunião. Isso não é
verdadeiro. Já sabemos que com certeza ela não participou. Então, vamos
acrescentar um F sobre o respectivo termo.
F
– “Se Divino participou da reunião, então Esmeralda também participou”;
– “Se Divino não participou da reunião, então Corifeu participou”;
– “Se Benivaldo ou Corifeu participaram, então Amarílis não participou”;
V
V participou da reunião”.
– “Esmeralda não
Instagram: @karinewaldrich
Facebook: @profkarinewaldrich
34
PROFESSORA: KARINE WALDRICH
Na primeira afirmação, temos o conectivo Se...então. Quando a segunda
proposição simples é Falsa, a primeira também deve ser, sob pena de termos a
situação proibida Se V então F. Voltando à tabela já apresentada,:
Se V então V = V
Se V então F = F
Se F então V = V
Se F então F = V
Podemos perceber que a única possibilidade de uma proposição deste tipo ser
falsa é quando o último termo é falso e o primeiro é verdadeiro.
O enunciado diz que todas as proposições são verdadeiras. Ou seja, elas não
podem assumir a forma:
Se V então F = F
Como o último termo da primeira proposição é falso, o primeiro só pode ser
falso, para que a proposição composta resultante seja verdadeira. Dessa
forma:
F
F
– “Se Divino participou da reunião, então Esmeralda também participou”;
– “Se Divino não participou da reunião, então Corifeu participou”;
– “Se Benivaldo ou Corifeu participaram, então Amarílis não participou”;
V
– “Esmeralda não participou da reunião”.
Se é falso que o Divino participou da reunião, como extraímos da primeira
proposição, então é verdadeiro que ele não participou. Já sabemos, então, que
é verdadeiro o primeiro termo da segunda proposição. Vamos completar:
Instagram: @karinewaldrich
Facebook: @profkarinewaldrich
35
PROFESSORA: KARINE WALDRICH
F
F
– “Se Divino participou da reunião, então Esmeralda também participou”;
V
– “Se Divino não participou da reunião, então Corifeu participou”;
– “Se Benivaldo ou Corifeu participaram, então Amarílis não participou”;
V
– “Esmeralda não participou da reunião”.
Agora chegamos a uma situação semelhante à anterior. Se a primeira parte da
proposição condicional é verdadeira, a segunda tem que ser verdadeira,
obrigatoriamente. Com isso, chegamos à conclusão de que Corifeu participou
da reunião, o que podemos completar também na terceira proposição:
F
F
– “Se Divino participou da reunião, então Esmeralda também participou”;
V
V
– “Se Divino não participou da reunião, então Corifeu participou”;
V
– “Se Benivaldo ou Corifeu participaram, então Amarílis não participou”;
V
– “Esmeralda não participou da reunião”.
A terceira proposição também é condicional (com o Se... então). Mas
percebam que o primeiro termo desta proposição também apresenta uma
proposição composta, a disjunção (com o “Ou”). Vimos, no início desta
questão, que basta um dos termos da disjunção serem verdadeiros para a
disjunção ser verdadeira:
ou V = V
V ou F = V
F ou V = V
F ou F = F
V
Instagram: @karinewaldrich
Facebook: @profkarinewaldrich
36
PROFESSORA: KARINE WALDRICH
Assim, como já sabemos que se o primeiro termo da condicional é verdadeiro,
o segundo também deve ser, temos:
F
F
–
“Se
Divino
participou”;
participou
da
reunião,
V
então
Esmeralda
também
V
V
– “Se Divino não participou da reunião, então Corifeu V
participou”;
V
– “Se Benivaldo ou Corifeu participaram, então Amarílis não participou”;
V
– “Esmeralda não participou da reunião”.
Com base nas frases acima, chegamos às seguintes conclusões:
•
•
•
•
Amarílis não participou;
Corifeu participou;
Divino não participou;
Esmeralda não participou.
Quanto à Benivaldo, não sabemos. Em termos lógicos, ele poderia ou não ter
participado, pois isso não afetaria a correção das frases do enunciado.
Mas já podemos responder à questão. Vamos para as alternativas:
“além de Esmeralda, não participaram de tal reunião
(A) Amarilis e Benivaldo (Amarílis não participou, Benivaldo não sabemos)
(B) Amarilis e Divino (Amarílis não participou, Divino não participou) –
VERDADEIRA
(C) Benivaldo e Corifeu (Benivaldo não sabemos, Corifeu participou) FALSA
(D) Benivaldo e Divino (Benivaldo não sabemos, Divino não participou)
(E) Corifeu e Divino (Corifeu participou, Divino não participou).
Assim, a letra B é o gabarito, pois temos certeza de que nem Amarílis nem
Divino participaram da reunião.
Instagram: @karinewaldrich
Facebook: @profkarinewaldrich
37
PROFESSORA: KARINE WALDRICH
Resposta: Letra B.
2009/FCC/TRE-PI/Ana. Jud.
Dadas as proposições simples p e q, tais que p é verdadeira e q é falsa,
considere as seguintes proposições compostas:
(1) p ^ q ; (2) ~p → q ; (3) ~(p v ~q) ; (4) ~(p ↔ q)
Quantas dessas proposições compostas são verdadeiras?
(A) Nenhuma.
(B) Apenas uma.
(C) Apenas duas.
(D) Apenas três.
(E) Quatro.
Essa questão traz as proposições em forma de símbolo, o que é bastante
recorrente em concursos da FCC.
O enunciado diz que p é verdadeira e q é falsa, e pede que analisemos as
proposições, para saber quantas proposições compostas são verdadeiras.
Vamos analisar cada proposição:
(2) p ^ q;
Como vimos acima, o símbolo ^ indica a Estrutura E...
Agora, vamos fazer na proposição do enunciado o que sempre fazemos,
sinalizando o valor lógico de cada proposição simples:
Fazendo como sempre fazemos:
V
F
p^q
Pela tabela do conectivo E, sabemos que a proposição composta só será
verdadeira se todas as proposições que a formarem forem também
verdadeiras. Ou seja, a proposição acima é falsa.
(3) ~p → q;
O ~ antes da proposição indica sua negação. ~p é a negação de p. Se p é
verdadeiro, ~p é falso.
Fazendo como sempre fazemos:
Instagram: @karinewaldrich
Facebook: @profkarinewaldrich
38
PROFESSORA: KARINE WALDRICH
F
F
~p → q
→
Também sabemos que
é o conectivo Se...então, e que proposições com
este conectivo só são falsas se a primeira parte for verdadeira e a segunda for
falsa. Logo, a proposição apresentada é verdadeira.
(4) ~(p v ~q);
Nesta proposição, a negação vem fora também. É como se fosse o -1 da
Matemática. Acharemos um valor para o que está dentro do parênteses, e a
resposta será o contrário (devido ao parênteses e a negação fora dele).
V
V
~(p v ~q)
Também sabemos que v é o conectivo Ou, e que proposições com este
conectivo só são falsas se ambas as proposições forem falsas.
Assim, o que está dentro do parênteses é verdadeiro. Mas fora dele há a
negação de tudo o que está dentro. Ou seja, a proposição é falsa.
(5) ~(p ↔ q)
Nesta proposição, também temos negação fora. O símbolo
Estrutura Se e somente se.
↔
indica
a
Passando à proposição proposta pelo enunciado, temos:
V
F
~(p ↔ q)
O conectivo se e somente se indica que são verdadeiras proposições
com termos de valor lógico igual – ou tudo verdadeiro, ou tudo falso.
Aqui temos um V e um F... ou seja, a parte dentro do parênteses é falsa.
Como há uma negação fora do parênteses, o resultado é a proposição toda ser
verdadeira.
Dessa forma, temos duas proposições verdadeiras.
Instagram: @karinewaldrich
Facebook: @profkarinewaldrich
39
PROFESSORA: KARINE WALDRICH
Resposta: Letra C.
2010/FCC/TRT 22a Região/Analista Judiciário
Considere um argumento composto pelas seguintes premissas:
- Se a inflação não é controlada, então não há projetos de
desenvolvimento.
- Se a inflação é controlada, então o povo vive melhor.
- O povo não vive melhor.
Considerando que todas as três premissas são verdadeiras, então, uma
conclusão que tornaria o argumento válido é:
(A) A inflação é controlada.
(B) Não há projetos de desenvolvimento.
(C) A inflação é controlada ou há projetos de desenvolvimento.
(D) O povo vive melhor e a inflação não é controlada.
(E) Se a inflação não é controlada e não há projetos de
desenvolvimento, então o povo vive melhor.
A questão fornece 3 premissas, necessariamente Verdadeiras:
-
-
Se a inflação não é controlada, então não há
desenvolvimento.
Se a inflação é controlada, então o povo vive melhor.
O povo não vive melhor.
projetos
de
Nessas horas, devemos procurar uma proposição simples que fornece a
base para as demais deduções.
Nessa questão, esta proposição é a última dada. “O povo não vive melhor”
é uma proposição simples, sem conectivo, em que é dada uma
informação necessariamente verdadeira.
Assim, vamos deduzir a conclusão a partir das outras premissas. Na segunda
proposição da segunda afirmação, é dito que o povo vive melhor. Isso é falso,
pela premissa que vimos acima, de que o povo não vive melhor.
Se a inflação não é controlada, então não há projetos de desenvolvimento.
Instagram: @karinewaldrich
Facebook: @profkarinewaldrich
Se a inflação é controlada, então o povo vive melhor.
40
PROFESSORA: KARINE WALDRICH
F
Se a primeira proposição da segunda afirmação for Verdadeira, teremos o caso
proibido Se V então F = F. Portanto, a primeira proposição da segunda
afirmação deve necessariamente ser Falsa:
Se a inflação não é controlada, então não há projetos de desenvolvimento.
F
F
Se a inflação é controlada, então o povo vive melhor.
Assim, deduzimos que a inflação não é controlada, o que pode ser utilizado na
primeira afirmação:
V
Se a inflação não é controlada, então não há projetos de desenvolvimento.
F
F
Se a inflação é controlada, então o povo vive melhor.
Chegamos novamente no caso proibido. A segunda afirmação deve
necessariamente ser Verdadeira, pois, do contrário, teremos uma situação em
que Se V então F = F, o que é proibido. Temos, então:
V
V
Se a inflação não é controlada, então não há projetos de desenvolvimento.
F
F
Se a inflação é controlada, então o povo vive melhor.
Portanto, passamos à análise das alternativas, sabendo que:
1) O povo não vive melhor (premissa dada pela questão);
2) A inflação não é controlada (primeira conclusão que chegamos);
3) Não há projetos de desenvolvimento (segunda conclusão
chegamos).
Instagram: @karinewaldrich
Facebook: @profkarinewaldrich
que
41
PROFESSORA: KARINE WALDRICH
(A) A inflação é controlada. (Falso)
(B) Não há projetos de desenvolvimento. (Verdadeiro).
(C) A inflação é controlada ou há projetos de desenvolvimento. (Como
vimos, uma proposição com a Estrutura Ou, para estar Verdadeira, precisa que
ao menos uma das proposições simples que a compõem seja
Verdadeira.
Nessa afirmação, temos:
A inflação é controlada: Falso, ela não é controlada.
Há projetos de desenvolvimento: Falso.
Portanto, a proposição é Falsa.)
(D) O povo vive melhor e a inflação não é controlada. (Aqui temos uma
proposição composta com a Estrutura E. Para a proposição com a Estrutura E
ser Verdadeira, as duas proposições que a compõem devem ser
Verdadeiras.
O povo vive melhor: Falso, pois o povo não vive melhor.
A inflação não é controlada: Verdadeiro.
Como uma das proposições é Falsa, a proposição O povo vive melhor e a
inflação não é controlada também é Falsa.)
(E) Se a inflação não é controlada e
desenvolvimento, então o povo vive melhor.
não
há
projetos
de
Aqui temos uma proposição composta com a Estrutura E dentro de outra com
a Estrutura Se...então. Nesses casos, primeiro resolvemos a Estrutura que
está dentro da outra. Assim, vamos resolver a Estrutura E para depois resolver
a Estrutura Se...então.
Temos:
A inflação não é controlada e não há projetos de desenvolvimento:
A inflação não é controlada: Verdadeiro.
Não há projetos de desenvolvimento: Verdadeiro.
Portanto, A inflação não é
desenvolvimento é Verdadeiro.
controlada
e
não
há
projetos
de
Passando à proposição maior:
Instagram: @karinewaldrich
Facebook: @profkarinewaldrich
42
PROFESSORA: KARINE WALDRICH
Se a inflação não é controlada e não há projetos de desenvolvimento,
então o povo vive melhor.
A primeira parte do Se...então está Verdadeira (como vimos acima). A
segunda parte (o povo vive melhor) é Falsa, pois já vimos que o povo não
vive melhor. Portanto, chegamos ao caso proibido, em que a proposição
composta é falsa. Assim, Se a inflação não é controlada e não há projetos
de desenvolvimento, então o povo vive melhor é Falso.)
Resposta: Letra B.
2009/FCC/TRE-GO/Téc. Jud.
Suponha que a seguinte afirmação é verdadeira:
“Se não vou viajar nas férias, então vivo menos.”
Uma sentença que equivale logicamente à afirmação dada é
(A) Se vou viajar nas férias, então vivo mais.
(B) Se vivo menos então não vou viajar nas férias.
(C) Não é verdade que, se vou viajar nas férias então vivo mais.
(D) Vou viajar nas férias e vivo mais.
(E) Vou viajar nas férias ou vivo menos.
A proposição proposta no enunciado é:
“Se não vou viajar nas férias, então vivo menos.”
Ela pode ser rescrita da seguinte forma:
Não vou viajar nas férias = p
Vivo menos = q
p→q
Vimos que esta proposição possui dois equivalentes:
~q → ~p e ~p v q.
Cada uma delas significa:
~q → ~p = Se não vivo menos então vou viajar nas férias.
~p v q = Vou viajar nas férias ou vivo menos.
Instagram: @karinewaldrich
Facebook: @profkarinewaldrich
43
PROFESSORA: KARINE WALDRICH
A segunda equivalente é exatamente a alternativa E.
Resposta: letra E.
2006/FCC/TRT-PE/Téc. Jud.
As afirmações seguintes são resultados de uma pesquisa feita entre
os funcionários de certa empresa.
Todo indivíduo que fuma tem bronquite.
Todo indivíduo que tem bronquite costuma faltar ao trabalho.
Relativamente a esses resultados, é correto concluir que
(A) existem funcionários fumantes que não faltam ao trabalho.
(B) todo funcionário que tem bronquite é fumante.
(C) todo funcionário fumante costuma faltar ao trabalho.
(D) é possível que exista algum funcionário que tenha bronquite e
não falte habitualmente ao trabalho.
(E) é possível que exista algum funcionário que seja fumante e não
tenha bronquite.
A questão diz que todo indivíduo que fuma tem bronquite. Ou seja, se a
pessoa fuma, ela tem bronquite. Mas ela pode ter bronquite e não fumar...
Perceberam que o número de pessoas que pode ter bronquite é maior do que o
número de pessoas que fuma? Justamente porque ela pode ter bronquite e não
fumar. Agora vamos representar essa conclusão em um diagrama:
Indivíduos com
bronquite
Indivíduos que
fumam
Em seguida, a questão comenta que todo indivíduo que tem bronquite costuma
faltar ao trabalho. Ou seja, pode haver faltas ao trabalho por diversos motivos,
um deles bronquite. Mas se o indivíduo tiver bronquite é fato: ele costumará
faltar ao trabalho.
Instagram: @karinewaldrich
Facebook: @profkarinewaldrich
44
PROFESSORA: KARINE WALDRICH
Ou seja, o “costuma faltar ao trabalho” engloba todos os indivíduos com
bronquite, que por sua vez engloba todos aqueles que costumam faltar ao
trabalho. No diagrama, temos:
Indivíduos que costumam
faltar ao trabalho
Indivíduos com
bronquite
Indivíduos que
fumam
Já sabemos que a palavra “Todo” sempre acompanha o evento que está
incluído em outro maior. Exemplo: Todo indivíduo que fuma tem bronquite.
Analisando as alternativas:
(F) existem funcionários fumantes que não faltam ao trabalho.
Para encontrar a resposta, utilizamos nosso diagrama. Vamos marcar um A
dentro de funcionários fumantes:
Indivíduos que costumam
faltar ao trabalho
Indivíduos com
bronquite
Indivíduos que
fumam
A
Instagram: @karinewaldrich
Facebook: @profkarinewaldrich
45
PROFESSORA: KARINE WALDRICH
Pelo diagrama, podemos ver que todos os indivíduos que fumam costumam
faltar ao trabalho. Logo, a alternativa está incorreta.
(G) todo funcionário que tem bronquite é fumante.
Vamos marcar um B no diagrama reservado aos indivíduos com bronquite,
para ver se eles compreendem os fumantes.
Indivíduos que costumam
faltar ao trabalho
Indivíduos com
bronquite
B
B
Indivíduos que
fumam
Pelo diagrama, podemos ver que podem existir funcionários com bronquite não
incluídos naqueles que fumam. Percebam que existem dois “Bs”: um incluído
também dentro daqueles que fumam, e um fora. Portanto, a assertiva está
errada.
(H) todo funcionário fumante costuma faltar ao trabalho.
Mais uma vez, veremos a assertiva no diagrama, indicando com um C:
Instagram: @karinewaldrich
Facebook: @profkarinewaldrich
46
PROFESSORA: KARINE WALDRICH
Indivíduos que costumam
faltar ao trabalho
Indivíduos com
bronquite
Indivíduos que
fumam
C
Não existe a possibilidade de haver indivíduos que fumam e que estejam foram
do círculo grande, que compreende os indivíduos que costumam faltar ao
trabalho.
Ou seja, essa é a alternativa correta.
(I) é possível que exista algum funcionário que tenha bronquite e
não falte habitualmente ao trabalho.
(J) é possível que exista algum funcionário que seja fumante e não
tenha bronquite.
Mais uma vez, recorremos ao diagrama, indicando com a letra D e E as
respectivas respostas:
Indivíduos que costumam
faltar ao trabalho
Indivíduos com
bronquite
D
E
Indivíduos que
fumam
Instagram: @karinewaldrich
Facebook: @profkarinewaldrich
47
PROFESSORA: KARINE WALDRICH
Vejam que todos os funcionários com bronquite se incluem nos que costumam
faltar ao trabalho. E todos os indivíduos que fumam se incluem nos que
possuem bronquite. Portanto, ambas alternativas estão erradas.
Resposta: Letra C.
2004/FCC/BAHIAGÁS/EPP
Considerando “todo livro é instrutivo”
verdadeira, é correto inferir que:
como
uma
proposição
(A) “Nenhum livro é instrutivo” é uma proposição necessariamente
verdadeira.
(B) “Algum livro é instrutivo” é uma proposição necessariamente
verdadeira.
(C) “Algum livro não é instrutivo” é uma proposição verdadeira ou
falsa.
(D) “Algum livro é instrutivo” é uma proposição verdadeira ou falsa.
(E) “Algum livro não é instrutivo” é uma proposição necessariamente
verdadeira.
Como sempre, vamos fazer o diagrama da proposição do enunciado: “Todo
livro é instrutivo”:
Instrutivo
Livro
Segundo o enunciado, essa é uma proposição
verdadeira. Agora analisamos as alternativas:
(A)
“Nenhum
livro
é
instrutivo”
necessariamente verdadeira.
é
necessariamente
uma
proposição
Nenhum livro é instrutivo significa:
Instagram: @karinewaldrich
Facebook: @profkarinewaldrich
48
PROFESSORA: KARINE WALDRICH
Livro
Instrutivo
É correto inferir isso? Não. Se todo livro é instrutivo, eles não podem estar
totalmente separados. Falso.
(B)
“Algum livro é instrutivo” é uma proposição necessariamente
verdadeira.
Instrutivo
Livro
Se todo livro é instrutivo, é necessariamente verdade que algum livro será
instrutivo.
Como vimos, a proposição Algum é ampla. Algum significa pelo menos
um. Podem até ser todos. A única coisa que o Algum indica é que pelo menos
um livro será instrutivo.
Alternativa correta.
(C)
“Algum livro não é instrutivo” é uma proposição verdadeira ou
falsa.
Essa questão já está incorreta mesmo sem analisar seu conteúdo. Proposição
verdadeira OU falsa, ligada pelo OU, indica que ou a proposição é verdadeira,
ou é falsa, ou é verdadeira e falsa (pelo menos uma das possibilidades,
podendo ser as duas).
Ocorre que pela aula 1, sabemos que não existe proposição verdadeira e
falsa ao mesmo tempo.
Alternativa falsa.
Instagram: @karinewaldrich
Facebook: @profkarinewaldrich
49
PROFESSORA: KARINE WALDRICH
(D)
“Algum livro é instrutivo” é uma proposição verdadeira ou
falsa.
Mesma explicação da alternativa anterior.
verdadeira e falsa ao mesmo tempo.
Não
existe
proposição
(E) “Algum livro não é instrutivo” é uma proposição necessariamente
verdadeira.
O enunciado diz que Todo livro é instrutivo.
Ou seja, podemos inferir que pelo menos um livro É instrutivo (como diz a
alternativa B).
Mas não é necessariamente verdade que algum livro NÃO É instrutivo. Porque
o que temos certeza é que todos os livros são instrutivos.
Resposta: Letra B.
2009/ESAF/MPOG/EPPGG
A negação de "À noite, todos os gatos são pardos" é:
a) De dia, todos os gatos são pardos.
b) De dia, nenhum gato é pardo.
c) De dia, existe pelo menos um gato que não é pardo.
d) À noite, existe pelo menos um gato que não é pardo.
e) À noite, nenhum gato é pardo.
Essa questão é da ESAF. Mas é muito boa, não achei nenhuma da FCC
parecida, por isso vou resolver na aula.
Além de falar sobre a negação dos termos Todo, Algum e Nenhum, ela
mostra que às vezes, com um pouco de malandragem, as bancas tentam
enganar o concurseiro. Vejamos:
A proposição proposta no enunciado é:
“À noite, todos os gatos são pardos.”
Se eu quiser negar essa preposição, posso falar “De dia, nenhum gato é
pardo”? Ou até mesmo “De dia, todos os gatos são pardos”?
Não.
Instagram: @karinewaldrich
Facebook: @profkarinewaldrich
50
PROFESSORA: KARINE WALDRICH
A questão tenta induzir o candidato a achar que a negação de “À noite” é “de
dia”. O que é errado.
Em questões anteriores, consideramos que a negação de “competente” é
“incompetente”, entre outras.
Mas essas são negações diretas, simples.
Outra coisa, muito diferente, e errada, é considerar contrários como
negação.
Por exemplo, menino e menina são contrários, não negação. Quente e frio são
contrários, mas não negação. Assim como noite e dia, caso desta questão.
Dito isso, já podemos excluir as alternativas A, B e C.
Agora, vamos falar sobre a negação do Todo, Algum e Nenhum.
Primeiramente, o Todo. Qual a negação de Todo A é B?
B
A
Podemos pensar que seria Nenhum A é B:
B
A
Mas vejam que não, necessariamente. Se houver algum A que não for B, a
frase Todo A é B já está falsa. Portanto, basta ter a certeza de que há
Algum A não é B.
Assim, a negação de Todo A é B é Algum A não é B.
~ (Todo A é B) = Algum
A não
éB
Instagram: @karinewaldrich
Facebook:
@profkarinewaldrich
51
PROFESSORA: KARINE WALDRICH
Por exemplo: Todo múltiplo de 100 é divisível por 5. A negação é Algum
múltiplo de 100 não é divisível por 5.
Agora passamos à negação do Algum. Algum A é B:
B
A
O Algum indica que pelo menos 1 A é B. A negação disso é dizer que nenhum
A é B. Como a palavra diz, nem-hum (nem um). São totalmente separados:
B
A
~ (Algum A é B) = Nenhum A é B
Já a negação do Nenhum é o contrário do que vimos acima. Negar que
Nenhum A é B é dizer que Algum A é B.
~ (Nenhum A é B) = Algum A é B
Agora vamos à resolução da questão. Já sabemos que as alternativas A, B e C
estão erradas.
A proposição é "À noite, todos os gatos são pardos".
Assim, vamos negar o Todo. Isso significa dizer que à noite, algum gato não é
pardo.
Instagram: @karinewaldrich
Facebook: @profkarinewaldrich
52
PROFESSORA: KARINE WALDRICH
A letra D diz isso. Ela diz que existe pelo menos um gato que não é pardo.
Resposta: letra D.
2009/FCC/MPE-AP/Téc. Adm.
Francisco, Carlos e Roberto são os únicos funcionários de um
escritório, sendo um deles digitador, outro montador de
computadores e o outro programador. A ficha de trabalho mostra que
um dos funcionários tem 28 anos, outro 30 anos e outro 35 anos. O
programador, que é amigo de Carlos, não é o mais velho de todos.
Roberto mexe em seu trabalho com parafusos, placas, fontes,
gabinetes e fios. Sabe-se ainda que o funcionário mais novo é
digitador.
Nas condições dadas, é correto afirmar que
(A) Francisco tem 30 anos e é digitador.
(B) Carlos tem 28 anos e é montador de computadores.
(C) Roberto tem 30 anos e é montador de computadores.
(D) Francisco tem 35 anos e é programador.
(E) Carlos tem 28 anos e é digitador.
Agora vamos passar para um outro tipo de questão.
São questões que trazem informações a serem cruzadas. Diante de várias
informações sobre coisas, pessoas, profissões, idades, e o que quer que seja,
você deve cruzar tais informações de modo a obter conclusões.
Nessa questão, temos os seguintes grupos de dados:
1) Existem três funcionários: Francisco, Carlos e Roberto;
2) Cada um deles possui uma profissão: digitador,
computadores e programador;
3) Cada um deles possui uma idade: 28, 30 ou 35 anos.
montador
de
Além disso, o enunciado fornece os seguintes cruzamentos de dados:
1) O programador não é Carlos;
2) O programador não é o mais velho;
3) Roberto mexe com parafusos, placas, fontes, gabinetes e fios (ou seja,
não digita nem programa, é o montador de computadores);
4) O funcionário mais novo é digitador.
Nesse tipo de questão, a resolução se dará por meio de uma tabela.
Instagram: @karinewaldrich
Facebook: @profkarinewaldrich
53
PROFESSORA: KARINE WALDRICH
É através dessa tabela que você cruzarão os dados. Na hora da prova, você vai
fazer a tabela na própria prova, do lado da questão. Assim como vai fazer com
os diagramas que vimos.
Na vertical da tabela, colocaremos o rol de funcionários, e na horizontal a
profissão e a idade. Da seguinte forma:
Nome/Profissão/Idade
Francisco
Carlos
Roberto
Digitador
Montador
Programador
28
30
35
Agora, vamos preenchendo a tabela de acordo com as informações do
enunciado.
Primeira informação:
1) O programador não é Carlos;
Colocamos essa informação na tabela da seguinte forma: é MENTIRA que
Carlos é o programador. Colocaremos um M (M de mentira) na célula da tabela
que cruza “Carlos” e “Programador”:
Nome/Profissão/Idade
Francisco
Carlos
Roberto
Digitador
Montador
Programador
28
30
35
M
2) O programador não é o mais velho;
Esta é uma informação que ainda não conseguimos colocar na tabela, pois não
há nenhuma célula cruzando essas informações.
3) Roberto mexe com parafusos, placas, fontes, gabinetes e fios (ou seja,
não digita nem programa, é o montador de computadores);
Como é VERDADE que Roberto é o Montador, colocamos um V (V de verdade)
na célula que cruza essas informações. E, se Roberto é o Montador, os outros
funcionários não são montadores. E nem Roberto é Digitador ou Programador.
Podemos preencher como M as respectivas células:
Nome/Profissão/Idade
Francisco
Carlos
Roberto
Digitador
M
Instagram: @karinewaldrich
Montador
M
M
V
Programador
28
30
35
M
M
Facebook: @profkarinewaldrich
54
PROFESSORA: KARINE WALDRICH
Agora, olhe para a tabela, mais especificamente para a linha com o nome de
Carlos. Você vê que é mentira que ele é o Montador ou o Programador. Ou
seja, ele só pode ser o Digitador...
Vamos preencher essa célula com um V. Também podemos preencher os
demais da coluna com M, afinal, se Carlos é digitador, ninguém mais é
digitador.
Nome/Profissão/Idade
Francisco
Carlos
Roberto
Digitador
M
V
M
Montador
M
M
V
Programador
28
30
35
M
M
Finalmente, na linha de Francisco, temos que é MENTIRA que ele é Digitador
ou Montador. Ou seja, ele é Programador. Podemos preencher com um V a
respectiva célula.
Nome/Profissão/Idade
Francisco
Carlos
Roberto
Digitador Montador
M
M
V
M
M
V
Programador
V
M
M
28
30
35
Assim, descobrimos as profissões de cada um:
• Francisco é o Programador;
• Carlos é o digitador;
• Roberto é o Montador.
Podemos, inclusive, voltar para a informação 2, que diz que o Programador
não é o mais velho. Isso significa que Francisco (o Programador) não possui 35
anos. Vamos completar a tabela:
Nome/Profissão/Idade
Francisco
Carlos
Roberto
Digitador Montador
M
M
V
M
M
V
Programador
V
M
M
28
30
35
M
Finalmente, passamos para a última informação.
4) O funcionário mais novo é digitador.
Sabemos que Carlos é o digitador. Ou seja, Carlos é o mais novo, possui 28
anos. Vamos completar a tabela, assinalando com um V essa célula e com um
M as células que trazem informação contrária:
Nome/Profissão/Idade
Francisco
Carlos
Roberto
Digitador Montador
M
M
V
M
M
V
Instagram: @karinewaldrich
Programador
V
M
M
28
M
V
M
30
M
Facebook: @profkarinewaldrich
35
M
M
55
PROFESSORA: KARINE WALDRICH
Agora, repare a linha de Francisco. Apenas a célula de 30 anos está vazia, e as
demais células de idade confirmam que ele não possui nem 28 nem 35 anos.
Ou seja, ele possui 30 anos. Podemos preencher essa célula com um V e a
célula que indica Roberto como tendo 30 anos com um M.
Nome/Profissão/Idade
Francisco
Carlos
Roberto
Digitador Montador
M
M
V
M
M
V
Programador
V
M
M
28
M
V
M
30
V
M
M
35
M
M
Finalmente, restou uma célula a ser preenchida, a que indica ter Roberto 35
anos.
Nome/Profissão/Idade
Francisco
Carlos
Roberto
Digitador Montador
M
M
V
M
M
V
Programador
V
M
M
28
M
V
M
30
V
M
M
35
M
M
V
Finalmente, a tabela está completa.
Esse é sempre o nosso objetivo preenchendo a tabela. Sempre completar
todas as informações da tabela.
Agora basta verificar que alternativa da questão bate com as informações da
tabela:
(F) Francisco tem 30 anos e é digitador.
Falso, o digitador é Carlos.
(G) Carlos tem 28 anos e é montador de computadores.
Falso, Carlos é o digitador.
(H) Roberto tem 30 anos e é montador de computadores.
Falso, Francisco tem 30 anos.
(I) Francisco tem 35 anos e é programador.
Falso, Francisco tem 30 anos.
(E) Carlos tem 28 anos e é digitador.
Resposta: Letra E.
2011/FCC/TRT-1a Região/ANALISTA JUDICIÁRIO
Instagram: @karinewaldrich
Facebook: @profkarinewaldrich
56
PROFESSORA: KARINE WALDRICH
Há dois casais (marido e mulher) dentre Carolina, Débora, Gabriel e
Marcos. A respeito do estado brasileiro (E) e da região do Brasil (R)
que cada uma dessas quatro pessoas nasceu, sabe-se que:
- Carolina nasceu na mesma R que seu marido, mas em E diferente;
- Gabriel nasceu no Rio de Janeiro, e sua esposa na Região Nordeste
do
Brasil;
- os pais de Marcos nasceram no Rio Grande do Sul, mas ele nasceu em
outra R;
- Débora nasceu no mesmo E que Marcos.
É correto afirmar que
(A)
(B)
(C)
(D)
(E)
Marcos nasceu na mesma R que Gabriel.
Carolina e Débora nasceram na mesma R.
Gabriel é marido de Carolina.
Carolina pode ser gaúcha.
Marcos não é baiano.
Mais uma questão como a anterior. Temos que organizar as informações que
são dadas para responder à questão.
Primeiramente, existem 4 pessoas, que podem ser de 4 estados, os quais
podem estar em 4 regiões diferentes. Podemos colocar isso na tabela, da
seguinte forma:
Nome
Carolina
Débora
Gabriel
Marcos
E1
E2
E3
E4
R1
R2
R3
R4
Chamei de E1, E2, etc, os estados possíveis, e de R1, R2, etc, as regiões
possíveis.
Agora, cabe a nós analisar cada informação que foi dada e tentar colocá-la na
tabela:
- Carolina nasceu na mesma R que seu marido, mas em E diferente;
Essa é uma informação para guardar para um momento futuro, pois não temos
como colocá-la na tabela agora.
- Gabriel nasceu no Rio de Janeiro, e sua esposa na Região Nordeste
do Brasil;
Instagram: @karinewaldrich
Facebook: @profkarinewaldrich
57
PROFESSORA: KARINE WALDRICH
Bem, vamos assumir que E1 = Rio de Janeiro:
Nome
Carolina
Débora
Gabriel
Marcos
E1 =
RJ
E2
E3
E4
V
M
M
M
R1
R2
R3
R4
Reparem na informação anterior e nessa. A informação anterior dizia que
Carolina nasceu na mesma região de seu marido. A informação atual diz que
Gabriel nasceu no Rio de Janeiro, e sua esposa na Região Nordeste. Ou
seja, Carolina não é a esposa de Gabriel...
Podemos colocar essa informação na tabela. Afinal, se Gabriel não é casado
com Carolina, é porque ele é casado com Débora, e Carolina é casada com
Marcos. Vamos chamar a região que Carolina e Marcos nasceram (é a mesma)
de R1, e a Região Sudesde (onde fica o RJ, o estado de Gabriel) de R2. Temos:
Nome
Carolina
Débora
Gabriel
Marcos
E1 =
RJ
V
E2
M
E3
M
E4
R1
M
R3
R4
V
R2 =
Sudes
te
M
M
M
M
V
V
M
M
M
M
M
- os pais de Marcos nasceram no Rio Grande do Sul, mas ele nasceu em
outra R;
A partir dessa frase, podemos assumir que:
1) Marcos e Carolina não nasceram no Rio Grande do Sul;
2) R1 (a mesma região que eles nasceram) não é a Região Sul.
Nome
Carolina
Débora
Gabriel
Marcos
E1 =
RJ
V
E2
M
E3
M
E4
R1 =
não é
a
Regiã
o Sul
V
R2 =
Sudes
te
R3
R4
M
M
M
M
V
V
M
M
M
M
M
M
- Débora nasceu no mesmo E que Marcos.
Instagram: @karinewaldrich
Facebook: @profkarinewaldrich
58
PROFESSORA: KARINE WALDRICH
Se Débora nasceu no mesmo E que Marcos, é porque é a mesma região que
ele. E, como Carolina nasceu na mesma região de Marcos, os três nasceram na
mesma Região. Reparem que a segunda informação dizia que a esposa de
Gabriel (já sabemos que é Débora) nasceu no Nordeste. Então, os 3 (Carolina,
Débora e Marcos) nasceram no Nordeste:
Nome
Carolina
Débora
Gabriel
Marcos
E1 =
RJ
V
E2
M
E3
M
E4
M
R1 =
R2 =
não é Sudes
a
te
Regiã
o Sul
=éo
Norde
ste
V
M
V
M
M
V
V
M
R3
R4
M
M
M
M
M
M
M
M
Voltando na primeira informação (lá em cima), que diz que Carolina nasceu na
mesma região que Marcos, mas em estado diferente, assumimos que o estado
de Marcos e Débora é E2, e de Carolina é E3:
Nome
Carolina
Débora
Gabriel
Marcos
E1 =
RJ
E2
E3
E4
M
M
V
M
M
V
M
V
V
M
M
M
M
M
M
M
R1 =
R2 =
não é Sudes
a
te
Regiã
o Sul
=éo
Norde
ste
V
M
V
M
M
V
V
M
R3
R4
M
M
M
M
M
M
M
M
Agora, com todas as informações ordenadas, passamos às alternativas:
(F)
Marcos nasceu na mesma R que Gabriel.
Marcos nasceu no Nordeste, e Gabriel no Sudeste. Alternativa falsa.
(G)
Carolina e Débora nasceram na mesma R.
Ambas nasceram no Nordeste. Alternativa correta.
(H)
Gabriel é marido de Carolina.
Gabriel é marido de Débora. Alternativa falsa.
Instagram: @karinewaldrich
Facebook: @profkarinewaldrich
59
PROFESSORA: KARINE WALDRICH
(I)
Carolina pode ser gaúcha.
Carolina nasceu no Nordeste. Ou seja, não pode ser gaúcha. Alternativa falsa.
(J)
Marcos não é baiano.
Não se pode afirmar que Marcos não é baiano, porque ele nasceu no Nordeste.
Pode ter nascido na Bahia sim. Alternativa falsa.
Resposta: Letra B.
Instagram: @karinewaldrich
Facebook: @profkarinewaldrich
60
PROFESSORA: KARINE WALDRICH
3. Memorex
TODO A É B:
EQUIVALENTE: SE A...ENTÃO B
NEGAÇÃO: ALGUM A NÃO É B
ALGUM A É B:
NEGAÇÃO: NENHUM A É B
NENHUM A É B:
EQUIVALENTE: SE A...ENTÃO ~B
NEGAÇÃO: ALGUM A É B
Instagram: @karinewaldrich
Facebook: @profkarinewaldrich
61