MATEMÁTICA

GEOMETRIA
ANALÍTICA
MATEMÁTICA
PROF CAIO
CIRCUNFERÊNCIA
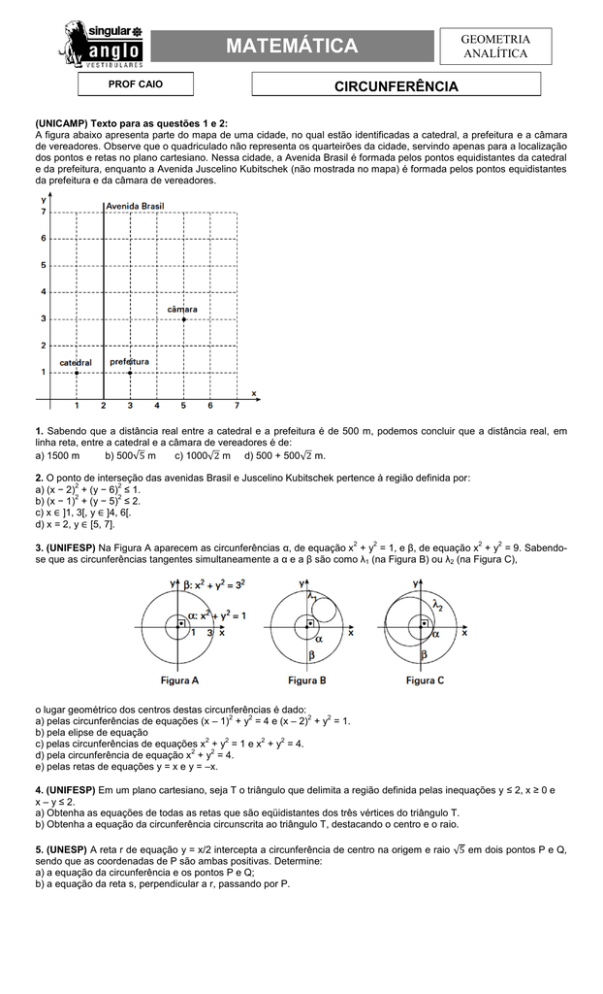
(UNICAMP) Texto para as questões 1 e 2:
A figura abaixo apresenta parte do mapa de uma cidade, no qual estão identificadas a catedral, a prefeitura e a câmara
de vereadores. Observe que o quadriculado não representa os quarteirões da cidade, servindo apenas para a localização
dos pontos e retas no plano cartesiano. Nessa cidade, a Avenida Brasil é formada pelos pontos equidistantes da catedral
e da prefeitura, enquanto a Avenida Juscelino Kubitschek (não mostrada no mapa) é formada pelos pontos equidistantes
da prefeitura e da câmara de vereadores.
1. Sabendo que a distância real entre a catedral e a prefeitura é de 500 m, podemos concluir que a distância real, em
linha reta, entre a catedral e a câmara de vereadores é de:
a) 1500 m
b) 500√5 m
c) 1000√2 m d) 500 + 500√2 m.
2. O ponto de interseção das avenidas Brasil e Juscelino Kubitschek pertence à região definida por:
2
2
a) (x − 2) + (y − 6) ≤ 1.
2
2
b) (x − 1) + (y − 5) ≤ 2.
c) x ∈ ]1, 3[, y ∈ ]4, 6[.
d) x = 2, y ∈ [5, 7].
2
2
2
2
3. (UNIFESP) Na Figura A aparecem as circunferências α, de equação x + y = 1, e β, de equação x + y = 9. Sabendose que as circunferências tangentes simultaneamente a α e a β são como λ1 (na Figura B) ou λ2 (na Figura C),
o lugar geométrico dos centros destas circunferências é dado:
2
2
2
2
a) pelas circunferências de equações (x – 1) + y = 4 e (x – 2) + y = 1.
b) pela elipse de equação
2
2
2
2
c) pelas circunferências de equações x + y = 1 e x + y = 4.
2
2
d) pela circunferência de equação x + y = 4.
e) pelas retas de equações y = x e y = –x.
4. (UNIFESP) Em um plano cartesiano, seja T o triângulo que delimita a região definida pelas inequações y ≤ 2, x ≥ 0 e
x – y ≤ 2.
a) Obtenha as equações de todas as retas que são eqüidistantes dos três vértices do triângulo T.
b) Obtenha a equação da circunferência circunscrita ao triângulo T, destacando o centro e o raio.
5. (UNESP) A reta r de equação y = x/2 intercepta a circunferência de centro na origem e raio √5 em dois pontos P e Q,
sendo que as coordenadas de P são ambas positivas. Determine:
a) a equação da circunferência e os pontos P e Q;
b) a equação da reta s, perpendicular a r, passando por P.
6. (UNESP) Seja C a circunferência de centro (2, 0) e raio 2, e considere O e P os pontos de interseção de C com o eixo
Ox. Sejam T e S pontos de C que pertencem, respectivamente, às retas r e s, que se interceptam no ponto M, de forma
que os triângulos OMT e PMS sejam congruentes, como mostra a figura a seguir.
a) Dê a equação de C e, sabendo que a equação de s é, y = x/3, determine as coordenadas de S.
b) Calcule as áreas do triângulo OMP e da região sombreada formada pela união dos triângulos OMT e PMS.
2
2
7. (UNESP) A distância do centro da circunferência x + 2x + y – 4y + 2 = 0 à origem é:
a) 3
b) √5
c) √3
d) √2
e) 1
8. (ESPM) Considere a região do plano cartesiano definida pelo sistema de inequações:
A área dessa região é igual a:
a) 4π/3
b) 2π/3 + √3
c) 4π - √3
2
d) 4π/3 + 1/2
e) 4π/3 + √3/2
2
9. (GV) Sabendo-se que a circunferência x + y – 6x + 4y + p = 0 possui apenas um ponto em comum com a reta de
equação y = x – 1, conclui-se que p é igual a:
a) 5
b) 7
c) 9
d) 11
e) 12
2
2
10. (GV) A equação da reta que passa pelo centro da circunferência x + y – x – 4y + 9/4 = 0 e é perpendicular à reta de
equação x = k (k é um número real) é:
a) y = 2
b) x + y = k
c) x = 2
d) x = 1/2
e) y = 1/2
11. (GV) No plano cartesiano, a circunferência que passa pelo ponto P(1, 3) e é concêntrica com a circunferência de
2
2
equação x + y – 6x – 8y – 1 = 0 tem a seguinte equação:
2
2
2
2
2
2
a) x + y + 6x + 8y – 40 = 0
b) x + y – 3x – 4y + 5 = 0
c) x + y – 6x – 8y + 20 = 0
2
2
2
2
d) x + y + 3x + 4y – 25 = 0
e) x + y – 3x + 4y – 19 = 0
2
2
12. (GV) No plano cartesiano, a equação de uma circunferência é (x – 2) + (y – 2) = 4. A reta t passa pelo ponto P e é
tangente a essa circunferência. P = (3; 2 + √3).
a) Represente a circunferência no plano cartesiano e determine a equação da reta que passa pelo centro da
circunferência e pelo ponto P.
b) Determine o coeficiente angular da reta t.
2
2
13. (FUVEST) A circunferência dada pela equação x + y – 4x – 4y + 4 = 0 é tangente aos eixos coordenados x e y nos
pontos A e B, conforme a figura. O segmento MN é paralelo ao segmento AB e contém o centro C da circunferência. É
correto afirmar que a área da região hachurada vale:
a) π – 2
b) π + 2
c) π + 4
d) π + 6
e) π + 8
2
2
14. (FUVEST) São dados, no plano cartesiano de origem O, a circunferência de equação x + y = 5, o ponto P = (1, √3)
e a reta s que passa por P e é paralela ao eixo y. Seja E o ponto de ordenada positiva em que a reta s intercepta a
circunferência. Assim sendo, determine:
a) a reta tangente à circunferência no ponto E.
b) o ponto de encontro das alturas do triângulo OPE.
2
2
15. (FUVEST) Considere, no plano cartesiano Oxy, a circunferência C de equação (x – 2) + (y – 2) = 4 e sejam P e Q
os pontos nos quais C tangencia os eixos Ox e Oy, respectivamente. Seja PQR o triângulo isósceles inscrito em C, de
base PQ, e com o maior perímetro possível. Então, a área de PQR é igual a:
a) 2√2 – 2
b) 2√2 – 1
c) 2√2
d) 2√2 + 2
e) 2√2 + 4
16. (FUVEST) No plano cartesiano Oxy, a circunferência C tem centro no ponto A = (–5, 1) e é tangente à reta t de
equação 4x – 3y – 2 = 0 em um ponto P. Seja ainda Q o ponto de intersecção da reta t com o eixo Ox. Assim:
a) Determine as coordenadas do ponto P.
b) Escreva uma equação para a circunferência C.
c) Calcule a área do triângulo APQ.
17. (FUVEST) No plano cartesiano Oxy, a reta de equação x + y = 2 é tangente à circunferência C no ponto (0,2). Além
disso, o ponto (1,0) pertence a C. Então, o raio de C é igual a:
3√2
5√2
7√2
9√ 2
11√2
a)
b)
c)
d)
e)
2
2
2
2
2
18. (FUVEST) No plano cartesiano, os pontos (0,3) e (-1,0) pertencem à circunferência C. Uma outra circunferência, de
centro em (-1/2, 4), é tangente a C no ponto (00,3). Então, o raio de C vale:
a)
√5
8
b)
√5
4
c)
√5
2
d)
3√5
4
e) √5
2
2
2
2
19. (INSPER) Na figura, a reta r é tangente às duas circunferências, de equações x + y = 16 e (x – 17) + y = 16.
Então, o coeficiente angular da reta r é igual a:
a) 3/4
b) 7/10
c) 5/13
d) 8/15
e) 7/25
20. (INSPER) No plano cartesiano, considere o triângulo ABC, sendo A = (0,0), B = (3√3, 3) e C = (0,6). Uma equação da
circunferência circunscrita ao triângulo ABC é:
3√3 2
2
2
2
2
2
a) (x – √3) + (y – 3) = 12
b) (x – √3) + (y – 3) = 9
c) (x –
) + (y – 3) = 27/4
2
3√3 2
2
2
2
d) (x – 3) + (y – √3) = 9
e) (x – 3) + (y –
) = 27/4
2
GABARITO
1. B
2. B
3. C
4. a) x = 2, y = 0 e y = x
2
2
5. a) x + y = 5, P = (2,1) e Q = (–2, –1)
2
2
6. a) (x – 2) + y = 4 e (18/5, 6/5)
7. B
8. E
9. A
10. A
11. C
12. a) y = √3.x + 2 – 2√3
13. B
14. a) x + 2y – 5 = 0
15. D
16. a) (–1, –2)
17. B
18. E
19. D
20. A
2
2
b) (x – 2) + y = 8, centro (2,0) e raio 2√2
b) y = –2x + 5.
b) 4/3 e 32/15
b) – √3/3
b) (2√3 + 1, 0)
2
2
b) (x + 5) + (y – 1) = 25
c) 25/4