Lista de Exercícios de Sinais Senoidais

Lista de Exercícios de Sinais Senoidais
Retificadores
(ENG - 20301)
Lista de Exercícios de Sinais Senoidais
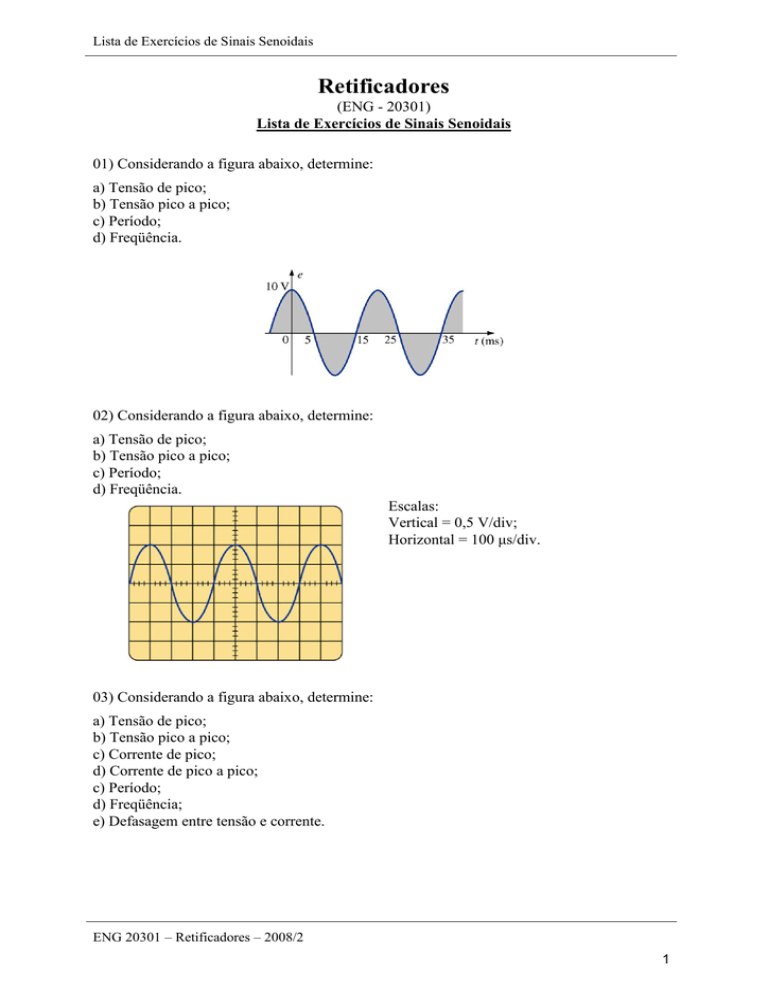
01) Considerando a figura abaixo, determine:
a) Tensão de pico;
b) Tensão pico a pico;
c) Período;
d) Freqüência.
02) Considerando a figura abaixo, determine:
a) Tensão de pico;
b) Tensão pico a pico;
c) Período;
d) Freqüência.
Escalas:
Vertical = 0,5 V/div;
Horizontal = 100 μs/div.
03) Considerando a figura abaixo, determine:
a) Tensão de pico;
b) Tensão pico a pico;
c) Corrente de pico;
d) Corrente de pico a pico;
c) Período;
d) Freqüência;
e) Defasagem entre tensão e corrente.
ENG 20301 – Retificadores – 2008/2
1
Lista de Exercícios de Sinais Senoidais
Escalas:
Vertical = 1 V/div;
Horizontal = 100 μs/div.
04) Considerando a figura a seguir, determine:
a) Tensão de pico;
b) Tensão pico a pico;
c) Expressão da função vt(t).
05) Para a forma de onda mostrada na figura abaixo, determine:
a) Tensão média;
b) Tensão eficaz.
ENG 20301 – Retificadores – 2008/2
2
Lista de Exercícios de Sinais Senoidais
06) Para a forma de onda mostrada na figura abaixo, determine:
a) Tensão média;
b) Tensão eficaz.
07) Para a forma de onda mostrada na figura abaixo, determine:
a) Período;
b) Quantos ciclos aparecem na figura;
c) Qual a freqüência em Hz;
d) Qual a velocidade angular;
e) Determine o valor de pico e o valor de pico a pico.
08) Para a forma de onda mostrada na figura abaixo, determine:
a) Período;
b) Quantos ciclos aparecem na figura;
c) Qual a freqüência em Hz;
d) Qual a velocidade angular;
e) Determine o valor de pico e o valor de pico a pico.
ENG 20301 – Retificadores – 2008/2
3
Lista de Exercícios de Sinais Senoidais
09) Se uma forma de onda periódica tem uma freqüência de 30 Hz, qual o tempo (em segundos)
necessário para completar 5 ciclos?
10) Qual a freqüência de uma onda periódica que completa 50 ciclos em 6 segundos?
11) Faça um esboço de uma onda quadrada periódica, que tenha uma freqüência de 10 kHz e
valor de pico de 5 V.
12) Para a forma de onda que aparece na tela de um osciloscópio mostrada abaixo, determine:
a) Valor de pico;
b) Período;
c) Freqüência;
d) Redesenhe esta forma de onda caso uma tensão de 100 mV fosse somada a ela.
Escalas:
Vertical = 100 mV/div;
Horizontal = 20 μs/div.
13) Faça a conversão de ângulos, conforme o caso:
a) 45o em radianos;
b) 60o em radianos;
c) π/4 em graus;
d) π/3 em graus;
e) 1,5 π em graus;
f) 280o em radianos.
14) Determine:
a) Velocidade angular de uma onda cujo período é 5 s;
b) Velocidade angular de uma onda cujo período é 100 ms;
c) Velocidade angular de uma onda cuja freqüência é 1000 Hz;
d) Freqüência de uma onda cuja velocidade angular é 600 rad/s;
e) Freqüência de uma onda cuja velocidade angular é 10 krad/s.
15) Se uma onda senoidal sofre uma variação de fase de 45o em 5 ms, determine a velocidade
angular desta onda.
ENG 20301 – Retificadores – 2008/2
4
Lista de Exercícios de Sinais Senoidais
16) Calcule a amplitude e a freqüência com base nas expressões a seguir:
a) 5  sen  377  t  ;
b) 5  sen  50  t  ;
c) 311 sen  t  ;
d) 1 cos  377  t  ;
e) 25  sen 100  t  .
17) Faça o esboço do gráfico da função 5  sen  377  t  usando como unidade do eixo das
abscissas (x):
a) Ângulo em graus;
b) Ângulo em radianos;
c) Tempo em segundos.
18) Se v  t   311 sen  377  t  , qual o tempo necessário (em segundos) para a onda completar
meio ciclo?
19) Com os dados abaixo, determine a expressão matemática da tensão senoidal.
v  t   50V para   30o e t  1ms .


20) Faça o esboço do gráfico da função 1 sen 377  t  45o usando como unidade do eixo das
abscissas (x):
a) Ângulo em graus;
b) Ângulo em radianos;
c) Tempo em segundos.
21) Determine a diferença de fase em milissegundos entre as seguintes formas de onda:


i  t   10  sen 1000  t  10 
v  t   50  sen 1000  t  30o
o
22) Para a tela do osciloscópio mostrada a seguir, determine:
a) Os períodos das duas ondas;
b) As freqüências da duas ondas;
c) Os valores eficazes das ondas;
d) A diferença de fase entre as mesmas.
ENG 20301 – Retificadores – 2008/2
5
Lista de Exercícios de Sinais Senoidais
Escalas:
Vertical = 0,25 V/div;
Horizontal = 500 μs/div.
23) Calcule o valor médio para as formas de onda abaixo:
24) Calcule o valor eficaz da forma de onda periódica abaixo:
25) Para cada uma das formas de onda vistas na figura abaixo, determine:
a) Período;
b) Freqüência;
c) Valor médio;
d) Valor eficaz.
ENG 20301 – Retificadores – 2008/2
6
Lista de Exercícios de Sinais Senoidais
Escalas:
Vertical = 20 mV/div;
Horizontal = 20 μs/div.
Escalas:
Vertical = 0,25 V/div;
Horizontal = 100 μs/div.
26) As expressões a seguir representam a tensão ou a corrente num resistor de 10 Ω. Determine a
expressão senoidal para a corrente ou tensão, conforme o caso:
a) v  t   150  sen  377  t  ;


c) i  t   2  sen 1000  t  30  ;
d) i  t   10  sen  377  t  90  .
b) v  t   10  sen 377  t  45o ;
o
o
27) Determine a reatância indutiva (em ohms) de um indutor de 5 H no caso de:
a) Corrente contínua;
b) 30 Hz;
c) 60 Hz;
d) 1 kHz.
28) Determine a indutância de um indutor cuja reatância é:
a) 10 Ω em f = 1 Hz;
b) 100 Ω em f = 100 Hz;
c) 150 Ω em f = 1 kHz.
29) Determine a freqüência para qual um indutor de 5 H apresenta as seguintes reatâncias:
a) 10 Ω;
b) 100 Ω.
30) São dadas a seguir expressões para a corrente ou tensão em uma reatância indutiva de 20 Ω.
Determine a expressão senoidal para a tensão ou corrente, conforme o caso.
a) v  t   150  sen  377  t  ;


c) i  t   2  sen 1000  t  30  ;
d) i  t   10  sen  377  t  90  .
b) v  t   10  sen 377  t  45o ;
o
o
31) Determine a reatância capacitiva (em ohms) de um capacitor de 100 μF no caso de:
a) Corrente contínua;
b) 30 Hz;
ENG 20301 – Retificadores – 2008/2
7
Lista de Exercícios de Sinais Senoidais
c) 60 Hz;
d) 1 kHz.
32) Determine a capacitância de um capacitor cuja reatância é:
a) 10 Ω em f = 1 Hz;
b) 100 Ω em f = 100 Hz;
c) 150 Ω em f = 1 kHz.
33) Determine a freqüência para qual um capacitor de 500 μF apresenta as seguintes reatâncias:
a) 10 Ω;
b) 100 Ω.
34) São dadas a seguir expressões para a corrente ou tensão em uma reatância capacitiva de 20 Ω.
Determine a expressão senoidal para a tensão ou corrente, conforme o caso.
a) v  t   150  sen  377  t  ;


c) i  t   2  sen 1000  t  30  ;
d) i  t   10  sen  377  t  90  .
b) v  t   10  sen 377  t  45o ;
o
o
35) No caso dos pares de expressões para tensão e corrente dados a seguir, indique se o
dispositivo envolvido é um capacitor, indutor ou resistor e os valores de C, L e R caso os dados
sejam suficientes:




b) v  t   550  sen  500  t  90  e i  t   2  sen  500  t  90  ;
c) v  t   5  sen  377  t  45  e i  t   1 sen  377  t  45  .
a) v  t   550  sen 377  t  60o e i  t   10  sen 377  t  30o ;
o
o
o
o
36) Em que freqüência a reatância de um capacitor de 1 μF é igual à resistência de um resistor de
2 kΩ?
37) A reatância de um indutor é igual à resistência de um resistor de 10 kΩ na freqüência de 5
kHz. Qual a indutância do indutor?
38) Determine a freqüência na qual um capacitor de 1 μF e um indutor de 10 mH têm a mesma
reatância.
39) Determine o valor da capacitância necessária para termos uma reatância capacitiva de mesmo
valor que a de uma bobina de 2 mH em 50 kHz.
40) Calcule a perda média de potência e o fator de potência para os circuitos nos quais a corrente
e a tensão de entrada são dadas pelas expressões a seguir:




a) v  t   50  sen   t  30o e i  t   10  sen   t  60o ;




b) v  t   50  sen   t  20o e i  t   2  sen   t  40o ;




c) v  t   50  sen   t  80o e i  t   3  cos   t  20o .
41) O fator de potência de um circuito é de 0,5 atrasado. A potência dissipada é de 500 W. Se a
tensão de entrada é dada por v  t   50  sen   t  30o , determine a corrente de entrada.


ENG 20301 – Retificadores – 2008/2
8
Lista de Exercícios de Sinais Senoidais


42) Na figura abaixo, e  t   100  sen 100  t  20o , determine:
a) A corrente i;
b) Calcule a indutância L;
c) Determine a potência média no indutor.


43) Na figura abaixo, i  t   5  sen 377  t  20o , determine:
a) A tensão e;
b) O valor da capacitância em μF;
c) Determine a potência média no capacitor.
44) Realize a conversão dos seguintes números, conforme o caso:
a) 4  j3 para a forma polar;
b) 2  j5 para a forma polar;
c) 2  j3 para a forma polar;
d) 6 30o para a forma retangular;
e) 2 45o para a forma retangular;
f) 10 60o para a forma retangular.
45) Realize as seguintes operações com números complexos:
a)  4  j3   2  j5 ;
b)  4  j3   2  j5 ;
c) 6 30o 10 90o ;
ENG 20301 – Retificadores – 2008/2
9
Lista de Exercícios de Sinais Senoidais
c)
100 45o
.
25 10o
46) Escreva as expressões a seguir na forma de fasores:

b) 2  5  sen  377  t  45  ;
c) 50  sen  377  t  0  ;
d) 2 10  cos  377  t  25  .
a)

2  220  sen   t  30o ;
o
o
o
47) Expresse os seguintes fasores relativos a correntes e tensões senoidais de 60 Hz:
a) I  40 30o A ;
b) I  0,05 20o A ;
c) V  220 0o V ;
d) V  1120o kV .
48) Para o sistema mostrado na figura a seguir, determine a expressão senoidal para a tensão
desconhecida va sabendo que:



ein  100  sen 377  t  20o e vb  10  sen 377  t  0o

49) Para o sistema mostrado na figura a seguir, determine a expressão senoidal para a corrente
desconhecida i1 sabendo que:



is  10 103  sen 377  t  90o e i2  3 103  sen 377  t  30o

ENG 20301 – Retificadores – 2008/2
10
Lista de Exercícios de Sinais Senoidais
50) Determine a expressão senoidal para a tensão aplicada e no sistema da figura abaixo:





va  10  sen 377  t  30o , vb  20  sen 377  t  20o e vc  40  sen 377  t  120o

52) Expresse as impedâncias dos componentes vistos na figura abaixo, tanto na forma polar
como na forma retangular.
53) Determine a corrente i nos elementos da figura abaixo usando álgebra dos números
complexos. Esboce as formas de onda de v e i no mesmo gráfico.
54) Determine a tensão v nos elementos visto na figura abaixo usando álgebra de números
complexos. Esboce as formas de onda de v e i no mesmo gráfico.
ENG 20301 – Retificadores – 2008/2
11
Lista de Exercícios de Sinais Senoidais
55) Calcule a impedância total dos circuitos vistos na figura abaixo. Expresse a resposta nas
formas retangular e polar e construa o gráfico das impedâncias.
56) Determine o tipo e o valor da impedância em ohms dos componentes dos circuitos em série
que devem estar no interior das caixas vistas na figura abaixo, considerando as tensões e
correntes indicadas.
57) Para o circuito da figura a seguir:
a) Determine a impedância total ZT na forma polar;
b) Construa o gráfico das impedâncias;
c) Determine o valor de C em microfaradas e o de L em henries;
d) Determine a corrente I e as tensões VR, VL e VC na forma fasorial;
e) Construa o diagrama de fasores para as tensões E, VR, VL e VC e a corrente I;
f) Calcule a potência média fornecida ao circuito;
g) Calcule o fator de potência do circuito e indique se ele é atrasado ou adiantado;
h) Determine as expressões senoidais para as tensões e a corrente;
i) Construa o gráfico das formas de onda das tensões e da corrente no mesmo gráfico.
ENG 20301 – Retificadores – 2008/2
12
Lista de Exercícios de Sinais Senoidais
58) Calcule as tensões V1 e V2 para os circuitos vistos na figura abaixo, em forma fasorial:
59) Para o circuito da figura a seguir:
a) Determine I, VR e VC em forma fasorial;
b) Calcule o fator de potência total indicando se é atrasado ou adiantado;
c) Calcule a potência média fornecida ao circuito;
d) Construa o diagrama de impedâncias;
e) Construa o diagrama de fasores para as tensões E, VR e VC e a corrente I.
60) Para o circuito da figura a seguir:
a) Determine a impedância total;
b) Determine IS, IC, IR e IL na forma fasorial;
b) Determine a potência média entregue pela fonte.
ENG 20301 – Retificadores – 2008/2
13
Lista de Exercícios de Sinais Senoidais
61) Para o circuito da figura a seguir:
a) Determine a impedância total;
b) A tensão sobre os elementos.
62) Para o circuito da figura a seguir:
a) Calcule E, IR e IL na forma fasorial;
b) Calcule o fator de potência total indicando se ele é atrasado ou adiantado;
c) Calcule a potência média fornecida ao circuito.
63) Para as telas de um osciloscópio de duplo traço ilustradas nas figuras abaixo, determine:
a) Diferença de fase entre as formas de onda, indicando qual está adiantada ou atrasada;
b) Determine os valores de pico a pico e eficaz de cada forma de onda;
c) Calcule a freqüência de cada forma de onda.
ENG 20301 – Retificadores – 2008/2
14
Lista de Exercícios de Sinais Senoidais
Escalas:
Vertical = 0,5 V/div;
Horizontal = 100 μs/div.
Escalas:
Vertical = 2 V/div;
Horizontal = 20 μs/div.
64) Para o circuito da figura abaixo, determine:
a) Calcule ZT;
b) Determine IS;
c) Calcule IC;
d) Calcule VL.
65) Para o circuito da figura abaixo, determine:
a) Calcule ZT;
b) Determine a corrente IS;
c) Calcule VC;
d) Calcule a potência média fornecida ao circuito.
ENG 20301 – Retificadores – 2008/2
15
Lista de Exercícios de Sinais Senoidais
66) Para o circuito da figura abaixo, determine:
a) Calcule ZT;
b) Determine a corrente IS;
c) Calcule I1 e I2 em forma fasorial;
d) Calcule as tensões V1 e Vab;
e) Calcule a potência média fornecida ao circuito;
f) Determine o fator de potência do circuito e indique se ele é atrasado ou adiantado.
67) Determine a potência média fornecida a R4 no circuito abaixo:
68) Para o conjunto de lâmpadas (puramente resistivas) ilustrado na figura abaixo:
a) Determine a potência total dissipada;
b) Calcule a potência total reativa e aparente;
c) Calcule a corrente IS;
d) Calcule a resistência de cada lâmpada para as condições de operação especificadas;
e) Determine as correntes I1 e I2.
ENG 20301 – Retificadores – 2008/2
16
Lista de Exercícios de Sinais Senoidais
69) Para o circuito da figura abaixo:
a) Determine a potência média fornecida a cada um dos componentes;
b) Calcule a potência reativa para cada componente;
c) Calcule a potência aparente de cada componente;
d) Determine a potência total em watts, volts-ampères reativos e volts-ampères e o fator de
potência FP do circuito;
e) Desenhe o triângulo de potências;
f) Calcule a energia dissipada pelo resistor em um ciclo completo da tensão de entrada.
70) Para o circuito visto na figura abaixo:
a) Calcule a potência média fornecida a cada elemento;
b) Determine a potência reativa para cada elemento;
c) Determine a potência aparente para cada elemento;
d) Calcule PT, QT, ST e FP para o sistema;
e) Desenhe o triângulo de potências;
f) Calcule IS.
71) Para o circuito visto na figura abaixo:
ENG 20301 – Retificadores – 2008/2
17
Lista de Exercícios de Sinais Senoidais
a) Calcule a potência média fornecida a cada elemento;
b) Determine a potência reativa para cada elemento;
c) Determine a potência aparente para cada elemento;
d) Calcule a potência total em watts, volts-ampères reativos e volts-ampères e o fator de potência
FP do circuito;
e) Desenhe o triângulo da potência.
72) A carga de um gerador de 120 V e 60 Hz é de 5 kW (resistiva0, 8 kVAR (indutiva) e 2 kVAR
(capacitiva):
a) Calcule o número total de kilovolts-ampères;
b) Determine o FP das cargas combinadas;
c) Calcule a corrente fornecida pelo gerador;
d) Calcule a capacitância necessária para estabelecer um fator de potência unitário;
e) Encontre a corrente fornecida pelo gerador com um fator de potência unitário e compare com o
valor obtido no item (c).
73) As cargas de uma fábrica ligada a um sistema de 1 kV, 60 Hz, são as seguintes:
 20 kW para aquecimento (fator de potência unitário);
 10 kW (Pi) para motores de indução (fator de potência 0,7 atrasado);
 5 kW para iluminação (fator de potência 0,85 atrasado).
a) Desenhe o triângulo de potência para a carga total;
b) Determine a capacitância necessária para tornar o fator de potência total igual a 1;
c) Calcule a diferença entre as correntes totais no sistema compensado e no sistema nãocompensado.
ENG 20301 – Retificadores – 2008/2
18