A Corrente Eléctrica de Magnetização e a Formação do Circuito

Caderno de Estudos de
nº 4
MÁQUINAS ELÉCTRICAS
A C o rre n t e E lé ct rica d e M ag n e t iz ação
e
A F o rmação do C ircu it o E q u ivale n t e
M an u e l V az Gu e d e s
(Prof. Associado com Agregação)
N ú cle o d e E st u d o s d e M áq u in as E lé ct ricas
Fa c u l d a d e d e E n g e n h a r i a d a Un i v e r s i d a d e d o P o r t o
Nos transformadores, o fluxo magnético, necessário ao funcionamento desta máquina eléctrica, é
mantido pela circulação permanente de uma corrente eléctrica — a corrente eléctrica de magnetização —
no enrolamento primário. Por isso, este fenómeno tem de aparecer representado em qualquer modelo
do transformador.
Devido ao carácter não linear das propriedades magnéticas do circuito magnético do transformador,
a forma de onda da corrente eléctrica de magnetização é não sinusoidal. Por isso, é não linear o circuito
eléctrico equivalente, capaz de modelizar os correspondentes fenómenos físicos, como o modelo que,
actualmente, é utilizado nos estudos do funcionamento em regime transitório de um transformador
aplicado em circuitos de medida, ou de protecção. Os conceitos envolvidos nesse tipo de modelização
analógica, servem, também, para o desenvolvimento de um modelo matemático programável para
integrar na simulação computacional dos regimes transitórios nos sistemas eléctricos.
Apesar dos problemas com a excitação do transformador, com a corrente de magnetização e com
as perdas no ferro já terem sido apresentados em diversos textos, [1] [2] [3], de uma forma que se tornou
clássica, actualmente, torna-se necessário a sua apresentação de uma forma que realce os problemas de
não linearidade, inerentes às necessidades de estudo do funcionamento de um transformador real nos
sistemas eléctricos contemporâneos.
1
A Corrente Eléctrica d e Magnetização
No transformador, a ligação magnética entre os enrolamentos é feita por um fluxo magnético
comum ψ(t), variável no tempo, que percorre um núcleo de material ferromagnético, e que é criado pela
Caderno de Estudos de MÁQUINAS ELÉCTRICAS, nº 4, pp. 3–13, Dezembro de 1992
2
A Corrente Eléctrica de Magnetização e A Formação do Circuito Equivalente
passagem de uma corrente eléctrica num dos enrolamentos que envolve o núcleo.
Quando o enrolamento indutor é formado por uma bobina de
fio condutor com N espiras, que envolve um núcleo maciço de
ψ
i
material ferromagnético, e que é percorrida por uma corrente eléctrica
de valor instantâneo i(t), cria-se uma força magnetomotriz, F = N·i, que
u
N
devido ao comprimento l do circuito magnético ser constante vai ser
responsável pelo aparecimento de um campo magnético de valor
H = N·i/l. Como o material do núcleo é ferromagnético, a relação entre
Circuito Magnético Maciço
o valor do campo magnético H e o valor da indução magnética B é não
linear. Como o circuito magnético tem uma secção constante S, a indução magnética vai ser responsável
pelo aparecimento de um fluxo de indução magnética totalizado ψ = B·S, que encadeia as N espiras do
enrolamento indutor. Não sendo iguais os fluxos de indução magnética através da cada uma das espiras
da bobina, considera-se φ = ψ/N como o fluxo de indução magnética médio por espira. Habitualmente,
considera-se que na situação de vazio o fluxo magnético de fugas ψf é nulo; nessa situação o fluxo que,
realmente, atravessa cada espira coincide com o fluxo médio por espira.
i
F
H
B
ψ
As relações entre as diversas grandezas que entram na caracterização do fenómeno da
magnetização de um circuito ferromagnético, como o que forma o núcleo de um transformador, provam
que há uma relação não linear ψ (i) entre o valor do fluxo magnético totalizado ψ e o valor da corrente
eléctrica que o cria i. Essa relação depende das propriedades do material ferromagnético que constitui o
núcleo, e é representada, com outras escalas, pela curva característica que relaciona a indução
magnética com o campo magnético B(H).
O núcleo do transformador é construído com materiais ferromagnéticos, isto é, com materiais que
adquirem uma magnetização elevada quando são submetidos a um campo magnético externo. Quando,
esses materiais são submetidos a uma primeira magnetização, para valores crescentes do campo
magnético H, a indução magnética B assume valores que se podem relacionar através de uma curva de
magnetização inicial, ou, simplesmente, curva de magnetização.
Uma curva de magnetização, para um
B
material ferromagnético, pode ser dividida
(T)
1,7
naturalmente em três regiões. Numa primeira
III
região (I) a curva parte da origem com uma
0,8
inclinação dada pelo valor da permeabilidade
magnético do vazio µo. Nesta região a curva
II
de magnetização é, usualmente, reversível.
Na
0,4
I
200
400
600
Curva de Magnetização
segunda
região
(II)
a
curva
de
magnetização tem uma grande inclinação e é,
H (A/m)
praticamente, rectilínea, mas irreversível. A
terceira região (III) da curva de magnetização é
separada da segunda por um “joelho”, e tem
2
3
A Corrente Eléctrica de Magnetização e A Formação do Circuito Equivalente
um andamento rectilíneo. Nesta terceira região, o valor da indução magnética é quase independente do
valor da intensidade do campo magnético e, portanto, a inclinação da curva é pequena, voltando a curva a
ser reversível numa grande extensão.
Este comportamento da curva de magnetização de um material ferromagnético resulta do
comportamento destes materiais durante a magnetização, principalmente do alinhamento dos pequenos
volumes de matéria onde os spins dos electrões estão espontaneamente alinhados — os domínios
(P. Weiss, 1906).
Depois de efectuada a primeira magnetização, a relação
entre o campo magnético e a indução por ele criada deixa de
B
Br
ser unívoca, porque para cada valor do campo magnético
existem dois valores da indução magnética, conforme aquele
H
Hc
valor está a aumentar ou a diminuir segundo uma variação
simétrica relativamente ao campo magnético nulo.
Nas
Br — Indução Remanente
magnetizações subsequentes, o andamento da característica
Hc — Força Coerciva
de magnetização dependerá das anteriores situações de
magnetização; porque o material irá conservar um “registo” do
Ciclo Histerético
seu anterior estado de magnetização — o valor da indução
remanente.
Assim, para uma magnetização alternada simétrica a relação entre os valores da indução magnética
e o valor do campo magnético que os cria B(H) é um ciclo fechado — o ciclo histerético.
Associado ao ciclo histerético de um material ferromagnético há uma
B
B1
informação sobre a densidade de energia posta em jogo durante o processo
de magnetização. Quando é feita uma magnetização por aplicação de um
H
0
H1
campo magnético alternado simétrico, durante a fase de crescimento do
campo, de 0 a H1, é consumida uma quantidade de energia por unidade de
volume de material que é dada por wmc = W/v =
⌠
⌡B 1 H dB , que é
0
proporcional à área limitada pelo ramo inferior do ciclo histerético, pelo semi-eixo positivo da indução
magnética e por um segmento de recta paralelo ao eixo das abcissas e que passa por B1.
Quando, na sequência da magnetização, o valor do campo é
diminuído de H1 até 0, é devolvida uma quantidade de energia por unidade
B
B1
de volume de material que é dada por wmd = W/v =
H
0
H1
⌠
⌡0 H dB , que é
B
1
proporcional à área limitada por um segmento de recta paralelo ao eixo das
abcissas e que passa por B1, pelo semi-eixo positivo da indução magnética e
pelo ramo superior do ciclo histerético. De uma forma análoga, e
devidamente adaptada, é possível verificar que ocorre algo semelhante durante a alternância negativa da
magnetização, 0 → – H1. Durante um ciclo de magnetização, é gasta no trabalho de orientação dos
domínios magnéticos uma quantidade de energia por unidade de volume proporcional à área contida no
interior do ciclo histerético.
No volume do material que constitui o núcleo magnético, esta energia é dissipada, sob a forma de
calor: constitui a energia de perdas por histerese. Quando o campo magnético indutor da magnetização
4
A Corrente Eléctrica de Magnetização e A Formação do Circuito Equivalente
é variável no tempo, periódico com uma frequência f, existem f ciclos de magnetização em cada segundo
e, consequentemente, haverá uma dissipação de energia devida à histerese magnética, com uma
densidade volúmica f·wm; isto é, as perdas por histerese são proporcionais à frequência de
magnetização.
Mas, devido à variação, no tempo, do campo magnético existem, também, perdas de energia
motivadas pelas correntes de Foucault.
A variação no tempo do fluxo magnético dá origem ao
aparecimento de um campo eléctrico no meio magnético do núcleo
(Lei de Faraday). Nesse meio, formam-se circuitos fechados, nos quais
ψ (t)
se induz uma força electromotriz, que é proporcional à frequência do
fluxo magnético indutor. A presença dessa força electromotriz
induzida, num circuito fechado, provoca a circulação de uma corrente
eléctrica. Ao conjunto dessas correntes eléctricas que aparecem no
Correntes de Foucault
material ferromagnético, percorrido por um fluxo magnético variável
no tempo, chama-se correntes de Foucault.
Como os circuitos fechados têm uma dada resistência
eléctrica, a circulação da corrente eléctrica nesses circuitos traduz-se por uma libertação de calor, por efeito Joule. A energia dissipada
ψ (t)
em calor constitui a energia de perdas por correntes de Foucault.
Uma forma de diminuir essas perdas de energia consiste na
diminuição do valor da corrente eléctrica através da diminuição do
comprimento dos circuitos fechados onde se induz a força
Correntes de Foucault
(Laminagem)
electromotriz; o que se consegue com a divisão da área transversa
em diversas pequenas áreas, por utilização de um material laminado.
O valor da corrente eléctrica também é diminuído, através do
aumento do valor da resistência do circuito fechado, por um aumento da resistividade do material ρ, o que
se consegue com a adição de substâncias (silício) ao ferro em fusão.
Como consequência do efeito magnético das correntes de Foucault, surge o efeito pelicular, que
provoca a alteração da distribuição da indução magnética, perto do centro da lâmina de material
ferromagnético, por acção do campo magnético de reacção criado por aquelas correntes parasitas. Este
efeito é pronunciado quando o campo magnético indutor tem uma frequência elevada (> 950 Hz;
19º harmónico).
À soma das perdas de energia, num transformador, motivadas pelo acção de um campo magnético
variável no tempo, devidas à histerese magnética do material ferromagnético e às correntes de Foucault
que circulam nesse material, chama-se perdas no ferro. A densidade volúmica destas perdas de energia
é dada por uma fórmula do tipo,
wFe = WFe/v = wh + wcF = k1·f·Bm2 + k2 ·f2·Bm2
Quando se procuram reduzir as perdas por correntes de Foucault, por utilização de um núcleo
formado por um empacotamento de lâminas de material ferromagnético, surge um outro problema que
tem influência no valor da corrente eléctrica de magnetização. Devido à forma como é realizado o
empacotamento da chapa, essencialmente, devido à impossibilidade de se obter um ajuste perfeito
5
A Corrente Eléctrica de Magnetização e A Formação do Circuito Equivalente
entre a chapa das colunas e das travessas, surgem pequenos entreferros nos percursos do fluxo
magnético. São zonas de permeabilidade magnética constante, mas baixa, µo = 4π·10–7 H/m, o que cria a
necessidade de uma corrente eléctrica de magnetização maior, para que nesses percursos o fluxo
magnético permaneça com o mesmo valor constante, que tem nos percursos feitos no interior do material
ferromagnético. Para além deste, existem, ainda, outros fenómenos com efeitos cumulativos, como o
desenvolvimento de correntes de Foucault entre lâminas, que ocorrem devido à execução do
empacotamento do núcleo. O valor do acréscimo da corrente eléctrica de magnetização depende de
muitos parâmetros construtivos: pressão do empacotamento, tolerâncias no corte da chapa, aspectos de
montagem do núcleo, etc…
Step–Lap Joint
Butt–Lap Joint
Os diferentes fenómenos inerentes à utilização de um núcleo formado por um empacotamento de
lâminas de material ferromagnético, traduzem-se, através dos contributos das suas componentes, nas
características da corrente eléctrica de magnetização: forma de onda, amplitude, esfasamento…
Como a relação entre o fluxo magnético totalizado e a corrente eléctrica que o cria — a corrente
eléctrica magnetizante [4, 05.25.115] — tem uma forma peculiar, um ciclo histerético, para o fluxo magnético
ter uma variação sinusoidal no tempo, a corrente eléctrica de magnetização apresenta uma variação não
sinusoidal.
φ
ψ1
φ
i1
ψ1
i1
i
i
0
t1
t
Construção Gráfica
A forma de onda da corrente magnetizante pode ser obtida através de uma construção gráfica, em
que nas respectivas escalas, são representadas as curvas de variação no tempo do fluxo totalizado ψ(t) e
a curva de variação do fluxo com a corrente ψ(i) para o material ferromagnético do núcleo. Fazendo
6
A Corrente Eléctrica de Magnetização e A Formação do Circuito Equivalente
corresponder, para um dado instante t1, o valor do fluxo indutor ψ1 e o valor corrente magnetizante
necessária para o criar iψ1, obtém-se um ponto (iψ1, t1) da curva de variação no tempo da corrente
magnetizante consumida para manter um determinado valor de fluxo no núcleo magnético, iψ. De uma
forma análoga podem ser determinados os pontos, da curva de variação da corrente eléctrica
magnetizante, correspondentes ao ciclo negativo do fluxo magnético.
Esta construção gráfica, com um carácter pedagógico notável, é actualmente substituída pela
determinação numérica da curva de variação da corrente magnetizante no tempo iψ(t), a partir da
expressão da variação no tempo do fluxo totalizado, ψ = ψm·cos(ωt), e da representação analítica do ciclo
histerético, através de funções exponenciais ψ = kr·(1–exp(–ks·iψ)), ou através de expressões
fraccionárias, ou através de séries de potências fraccionárias iψ = ∑r kr·ψαr, com αr < 1 . Normalmente, o
ciclo histerético encontra-se globalmente definido por várias expressões analíticas, válidas apenas para
uma gama de valores da corrente eléctrica magnetizante. Obtém-se, por cálculo, uma amostragem dos
valores da forma de onda da corrente eléctrica magnetizante, iψk(tk).
A forma de onda da corrente magnetizante, tem um andamento não sinusoidal. Devido à simetria
do ciclo histerético a forma de onda é constituída por duas semi-ondas com igual andamento, mas de
sinal contrário. Uma análise harmónica desta onda [5], permite verificar que devido à semi-onda positiva
ter andamento igual à semi-onda negativa, ela não possui termo contínuo, e apenas possui termos
harmónicos de ordem ímpar, e, na situação em estudo em que há simetria da onda da corrente eléctrica
relativamente ao eixo das ordenadas, essa onda apenas possui termos com variação em cosseno.
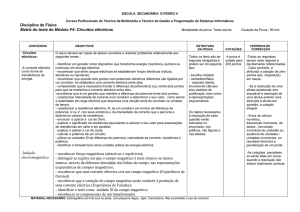
Verifica-se, ainda que a forma de onda da corrente eléctrica magnetizante possui um valor de pico
elevado, e que existe um ângulo de esfasamento entre a corrente eléctrica e o fluxo magnético: o ângulo
de atraso magnético. Também os termos harmónicos além da amplitude decrescente com a ordem do
harmónico, possuem um esfasamento (phase) próprio ϕh.
Uo = 55,7 V
Io = 1,66 A
Po = 12,5 W
h
1
3
5
7
9
11
13
|ih| A
1,99
1,03
0,22
0,06
0,04
16·10-3
12·10-3
/ ih °
– 1 1 8,5
– 9,9
100,3
46,6
147,2
105,6
– 172,1
Núcleo Ferromagnético Saturado
A importância dos termos harmónicos componentes da forma de onda de corrente eléctrica
magnetizante é grande, sendo habitual salientar-se as consequências da existência do terceiro
harmónico. Nos transformadores trifásicos de potência a possibilidade de circulação desse terceiro
harmónico condiciona a escolha do tipo de ligação das bobinas dos enrolamentos do transformador,
devido aos problemas criados nas redes de telecomunicações pela circulação do terceiro harmónico nas
linhas de transporte de energia. Nos transformadores de sinal, a existência de uma terceiro harmónico na
corrente magnetizante, com uma frequência tripla da frequência do termo fundamental e esfasado
relativamente a esse termo, pode provocar problemas de distorção no sinal. Em qualquer destas
situações, a existência de termos harmónicos com diferentes frequências pode provocar problemas de
ressonância, para qualquer uma dessas frequências, no circuito eléctrico em que está inserido o
transformador.
Quando, por simplificação, se considera que o ciclo histerético de um material ferromagnético tem
A Corrente Eléctrica de Magnetização e A Formação do Circuito Equivalente
7
um andamento esbelto, em que o valor da força coerciva Hc é muito inferior ao valor do campo magnético
de saturação Hs, e, apenas, se considera representada pela curva de magnetização a variação do fluxo
magnético com a corrente eléctrica ψ(i), pode-se determinar a forma de onda da corrente magnetizante
por uma construção gráfica análoga à anterior, ou por meio de determinação numérica, a partir das
expressões representativas das relações entre as grandezas envolvidas, t, ψ, iψ.
Uma forma analítica de representar a
relação i(ψ)
é
através
incompleto
de
da
um
polinómio
forma
i = α·ψ + ß·ψ2m+1, com m>1 {m=3 ; m=4 ; m=5 },
(ver Apêndice). Com uma expressão deste tipo,
torna-se
fácil
elaborar
um
programa
de
computador capaz de determinar valores da
corrente magnetizante e proceder à respectiva
análise harmónica [5].
Programa CORMAG
Definir constantes pi, f, psim, m, np
Dimensionar as matrizes i( ), psi( ), a( ), ik( )
Ler os np valores de i( ) e psi( )
Chamar subrotina MINQUA9(m,np,i( ),psi( ),
Para cada valor do tempo tk
psi = psim*cos(2*pi*f*tk)
ik(tk) = a(1)*psi + a(2)*psi
↑m
repetir
Chamar FOURIER_1
4, p. 21] !%
Imprimir tk, ik( ), Bh( ), Ch( )
Fim
Nas condições desta hipótese de estudo,
a forma de onda de variação da corrente eléctrica magnetizante iψ(t), ainda está representada por uma
forma de onda não sinusoidal, com termos harmónicos de ordem ímpar e com variação em cosseno, mas
o ângulo de atraso magnético é nulo, isto é, não existe esfasamento entre o fluxo magnético e a corrente
eléctrica de magnetização. Note-se, que no estudo computacional apresentado podem surgir outros
termos harmónicos, não previstos, mas resultantes de uma má aproximação da característica de
magnetização pela expressão analítica apresentada.
Nesta aproximação à realidade, a curva de magnetização ainda possui termos harmónicos, com
importância nas aplicações do transformador tanto para potências elevadas, como no domínio do sinal.
Uma última hipótese de estudo, consiste em considerar que durante todo o regime de
funcionamento do transformador não ocorre saturação magnética, ou que o seu ponto de
funcionamento está sempre colocado na parte rectilínea da característica de magnetização (zona II).
Nessa hipótese de estudo, a característica de magnetização é linear, e consequentemente a forma de
onda da corrente magnetizante é sinusoidal. Tal pode ser verificado por construção gráfica, ou por um
simples programa de computador…. Esta situação de estudo, que não corresponde à realidade do
funcionamento do transformador, pode ser necessária para aplicação de métodos de tratamento
analítico, como o método simbólico de representação de grandezas sinusoidais, ou para permitir a
representação das relações do fluxo magnético com a corrente eléctrica que o cria, através de parâmetros
(indutâncias) constantes, como ocorre em certas aplicações da Teoria Generalizada das Máquinas
Eléctricas.
Para que exista um determinado fluxo magnético ψ(t), com variação sinusoidal no tempo, no núcleo
do transformador é necessário que seja fornecido ao transformador uma corrente eléctrica magnetizante
iψ(t), que tem uma variação no tempo não sinusoidal. Mas a presença do fluxo magnético variável no
tempo, no núcleo ferromagnético do transformador, provoca o aparecimento de correntes de Foucault,
com um valor proporcional à variação do fluxo no tempo, mas com um sentido tal que cria uma força
magnetomotriz com um sentido, que se opõe ao da variação do fluxo magnético ψ. Essa acção tem de
ser contrariada por uma componente sinusoidal da força magnetomotriz, criada por uma corrente eléctrica
sinusoidal, com a mesma frequência que o fluxo magnético, que tem de ser fornecida ao transformador.
A Corrente Eléctrica de Magnetização e A Formação do Circuito Equivalente
8
Só desta forma o fluxo magnético permanece no valor necessário para criar uma força electromotriz, e(t) =
= – dψ/dt, no enrolamento indutor, que verifique a equação eléctrica do enrolamento: u = Ri – e. Existe,
por isso, uma componente sinusoidal da corrente eléctrica de magnetização icF(t) que está em fase com a
força electromotriz induzida e(t), e em quadratura avanço sobre o fluxo magnético ψ(t). Desta forma
verifica-se para a corrente de magnetização i(t) que: i(t) = iψ(t) + icF(t). Por isso, a corrente final mantem-se
distorcida, e aumenta o ângulo de atraso magnético.
Mas devido à construção laminada do núcleo do transformador, mesmo quando efectuada com a
melhor tecnologia (step-lap joint) e cuidado, existe a necessidade de fornecer uma corrente eléctrica de
magnetização superior ao valor necessário para contrariar a acção das correntes de Foucault e para criar
uma determinada onda sinusoidal de fluxo. Esse valor que depende do tipo, e modo, de construção do
núcleo, pode ser determinado por curvas de magnetização para os entreferros (joint), próprias para o tipo
de construção do núcleo utilizado, [1, p. 10]. Assim, o valor da corrente de magnetização, é:
i(t) = iψ(t) + icF(t) + nj·iψj(t)
não ultrapassando um valor de 5 % do valor da corrente do enrolamento, quando está alimentado pela
respectiva tensão nominal. Por exemplo, para um transformador de distribuição trifásico actual com
isolamento seco, (500 kVA, 15 000/400 V, Dy11, 50 Hz), verifica-se que a corrente de magnetização
i ≅ Io2 = 10,47 A (1,45 %). Para um transformador com uma capacidade inferior a 1 kVA, aquela relação
entre correntes eléctricas pode ser bastante diferente.
A
A determinação da corrente eléctrica, necessária à
W
manutenção de um determinado fluxo magnético no núcleo
V
f
real de um transformador, pode ser feita recorrendo ao cálculo
através das curvas características das propriedades do material
ferromagnético, ou por via experimental, mediante uma
montagem de medida análoga à figurada [6, § 8.2]. Só há que
Circuito de Medida
atender ao carácter não linear da corrente eléctrica de
magnetização, e, consequentemente, utilizar aparelhos de medida adaptados a uma onda não
sinusoidal.
Em todo este estudo considerou-se que o fluxo magnético tinha uma variação sinusoidal no
tempo. Actualmente, devido à poluição harmónica introduzida nas redes eléctricas por cargas não
lineares, sucede que a tensão de alimentação do transformador, e, portanto, o fluxo magnético são não
sinusoidais. Nessa situação, todos os fenómenos descritos vêm agravados, e as Normas [6, § 8.4]
prevêem a redução da corrente eléctrica de magnetização a uma base de tensão sinusoidal.
Conhecida a forma de variação no tempo da corrente eléctrica de magnetização, assim como os
fenómenos que ocorrem num núcleo de material ferromagnético laminado, resta procurar um modelo
que permita efectuar estudos sobre o funcionamento de transformadores em qualquer regime:
permanente ou transitório. Esse modelo, independentemente do seu tipo, deve representar os
fenómenos característicos do funcionamento do núcleo: a criação do fluxo magnético, e as perdas de
energia inerentes à situação física daquela criação.
Quando se considera que o transformador está a funcionar na zona linear da característica de
magnetização e se desprezam os efeitos dos entreferros do circuito magnético, e que portanto a
corrente eléctrica magnetizante é sinusoidal, mas que existem perdas magnéticas, devidas às correntes
9
A Corrente Eléctrica de Magnetização e A Formação do Circuito Equivalente
de Foucault, resulta que a corrente de eléctrica de magnetização é sinusoidal e i ≡ Io, considerando-se
como resultante da adição de duas componentes, Io = Im + Ia: uma, a corrente eléctrica magnetizante Im,
que é responsável pela criação do fluxo magnético, e a outra, a corrente eléctrica de perdas, que é
responsável pelas perdas no circuito magnético, Ia. A corrente de perdas está em fase com a força
electromotriz e em quadratura avanço sobre a componente magnetizante da corrente de magnetização,
que nesta situação está em fase com o fluxo magnético.
Este modelo descritivo, pode traduzir-se por um outro modelo —
Io
um circuito eléctrico de parâmetros concentrados — que apresente um
Ia
Im
R
L
comportamento eléctrico análogo ao do núcleo do transformador. A
adição das duas componentes sugere que o circuito eléctrico é formado
por um paralelo de dois ramos de circuito eléctrico, um, puramente
óhmico, onde circula a corrente eléctrica de perdas Ia, o outro,
puramente indutivo, onde circula a corrente magnetizante Im. Ao circuito
encontra-se aplicada uma tensão igual ao valor da força electromotriz que se induz no respectivo
enrolamento.
Quando se considera que as propriedades do circuito magnético ficam integralmente
representadas pela característica de magnetização, a corrente eléctrica magnetizante tem um forma de
onda distorcida, e sendo decomposta em série de termos harmónicos verifica-se que é formada por um
conjunto de termos de ordem ímpar. Par que a corrente eléctrica de magnetização (= iψ(t) + icF(t) + nj ·iψj (t))
pudesse ser representada por uma corrente eléctrica sinusoidal era necessário que essa corrente
eléctrica produzisse os mesmos efeitos que a corrente de magnetização, o que implica que se procure
uma corrente eléctrica com o mesmo valor eficaz. Assim, passa-se a considerar que o núcleo é percorrido
por uma corrente eléctrica sinusoidal com o valor eficaz da corrente eléctrica de magnetização,
Ief =
∑ h I2hef , formada por duas componentes ( Im, Ia), e utiliza-se um circuito eléctrico equivalente
análogo ao primeiro.
io (t)
ia (t)
Im
Mas, a presença dos termos harmónicos de mais alta frequência
(h > 9), apesar da sua pequena amplitude, traduzir-se-ia por um
aumento de perdas magnéticas com a frequência, que o modelo não
representa. Há, para isso, que substituir a resistência linear por uma
Rnl
L
resistência não linear. Este modelo poderia representar o núcleo de
um transformador com consideração da influência das frequências
presentes na corrente eléctrica de magnetização, quando o fluxo magnético é sinusoidal. Isso exigia que
as restantes resistências eléctricas existentes no transformador, principalmente a resistência do
enrolamento primário, fossem modelizadas atendendo ao seu comportamento real face à frequência dos
diferentes harmónicos presentes na corrente eléctrica.
Quando
existe a necessidade
de
considerar
o
real
io (t)
ia (t)
comportamento do núcleo do transformador, então a corrente
eléctrica de magnetização tem de ser representada pelo seu valor
instantâneo io(t) ≡ i(t), que corresponde à adição de uma corrente
devida ao efeito das correntes de Foucault, com uma forma de onda
não sinusoidal da corrente eléctrica magnetizante necessária para
Rnl
i m (t)
A Corrente Eléctrica de Magnetização e A Formação do Circuito Equivalente
10
criar o fluxo sinusoidal ψ. Esta corrente só pode resultar da aplicação de uma tensão sinusoidal, igual à
força electromotriz induzida no enrolamento primário e(t), a uma bobina não linear. Resulta assim um
circuito eléctrico equivalente não linear, com os parâmetros concentrados definidos por expressões
analíticas, do tipo : iψ = ∑r kr·ψαr, e icF = kcF·eß+ ic.
Com este modelo perde-se o interesse, e a simplicidade, característicos do circuito eléctrico
equivalente quando utilizado na modelização de um fenómeno físico, envolvendo circuitos eléctricos.
Existe, por isso, a necessidade de desenvolvimento de um modelo puramente computacional, que
poderá ter um carácter qualitativo, mas que, mesmo quando for apenas quantitativo será complicado e de
difícil determinação das expressões que definem os parâmetros.
Os modelos apresentados tornar-se-iam ainda mais complicados se fosse considerado
comportamento não sinusoidal da tensão de alimentação de algumas redes eléctricas, e, portanto do
fluxo magnético. Nessa situação, o valor das perdas magnéticas, que dependem do valor da indução
magnética, seria afectado pela amplitude dos harmónicos e pelo seu esfasamento, o que complicaria as
respectivas expressões analíticas.
Os circuitos equivalentes apresentados podem ser utilizados na análise do funcionamento dos
transformadores de medida, em regime transitório, desde que não se considere que o regime de
funcionamento altera o valor da indução remanente, ou, na sua forma computacional, podem ser
integrados nos programas de análise do regime transitório de sistemas eléctricos.
3
Conclusão
Devido às características não lineares das propriedades magnéticas dos materiais ferromagnéticos
utilizados nos núcleos dos transformadores a corrente eléctrica de magnetização necessária à criação e
manutenção do fluxo magnético, é não sinusoidal e existem perdas magnéticas, por histerese e por
correntes de Foucault.
A consideração destas correntes eléctricas não sinusoidais, e das perdas de energia permite o
desenvolvimento de modelos do fenómeno de magnetização do núcleo do transformador, que
representam integralmente as reais condições de magnetização. Abandonando considerações
simplificativas usuais, surgem novos modelos, baseados em circuitos eléctricos equivalentes de
parâmetros concentrados, mas não lineares, que podem representar os fenómenos principais. Surgem,
também, modelos computacionais que apenas estabelecem relações entre expressões analíticas, de
difícil determinação…
Mas, as modernas condições de exploração dos sistemas eléctricos, e o regime de funcionamento
transitório de alguns transformadores, impõem uma adopção criteriosa destes modelos.
Referências
Bibliográficas
[1]
E. E. Staff MI T; Magnetic Circuits and Transformers, MIT Press 1943
[2]
L. F. Blume A. Boyajian G. Camilli; Transformer Engineering, John Wiley & Sons 1958
[3]
Carlos Castro Carvalho; Transformadores, AEFEUP 1983
[4]
CEI–05; Vocabulaire Electrotechnique Internationale — Définitions Fondamentales, CE I 1954
[5]
Manuel Vaz Guedes; Grandezas Periódicas Não Sinusoidais, NE ME 1992
[6]
ANSI/IEEE C57.12.90; IEEE Standard Test Code for Liquid–Immersed Distribution, Power, and Regulating
Transformers and…, IEEE 1987
[7]
Manuel Vaz Guedes; Métodos Numéricos Para Análise do Campo Magnético das Máquinas Eléctricas,
dissertação de doutoramento, FEUP 1983
11
A Corrente Eléctrica de Magnetização e A Formação do Circuito Equivalente
Apêndice
ψ ) de um Material Ferromagnético
Aproximação da Curva i(ψ
Quando se considera a natureza não linear
das propriedades de um material magnético,
torna-se, frequentemente, necessário conhecer
uma expressão algébrica que represente
precisamente aquela curva característica.
Programa MINQUA9
Definir constantes m, np
Dimensionar as matrizes i( ), psi( ), S( ), t( ), a( )
Ler os np valores de i( ) e psi( )
Anular os elementos de [S] e {t}
Para cada ponto ip até np
S(1,1) = S(1,1) + psi(ip)*psi(ip)
pk = psi(ip)
↑(2*m+1)
S(1,2) = S(1,2) + pk*psi(ip)
S(2,2) = S(2,2) + pk*pk
t(1) = t(1) + i(ip)*psi(ip)
t(2) = t(2) + i(ip)*pk
repetir
S(2,1) = S(1,2)
denom = S(1,1)*S(2,2) – S(2,1)*S(1,2)
!%*
Cramer
a(1) = (t(1)*S(2,2) – t(2)*S(1,2))/denom
alfa
!%*
a(2) = (S(1,1)*t(2) – S(2,1) *t(1))/denom
beta
!%*
Imprimir a(1), a(2)
Fim
Existem vários tipos de expressões que
permitem aproximar a curva de magnetização:
expressões algébricas, ou transcendentes, do
tipo funções spline, [7].
Um tipo de expressões, de cómoda utilização
na representação da relação i(ψ), são as
expressões polinomiais completas, de terceira
ou de quarta ordem, que apresentam a
vantagem de
poderem
ser
facilmente
diferenciadas ou integradas: i = ∑ r a r ·ψr . O
critério de aproximação utilizado pode ser o que
resulta da aplicação do método dos mínimos
quadrados.
No entanto, na utilização da expressão
polinomial completa verifica-se que existem
alguns membros que têm parâmetros ar com valores numéricos muito pequenos. Por isso, na aproximação da curva
i(ψ) também se utiliza uma expressão polinomial reduzida, como:
i = α·ψ + ß·ψ2m+1
com m>1,
{ m=3, m=4, m=5}
A determinação dos parâmetros {α, ß} é feita com a utilização do método dos mínimos quadrados. Pretende-se
minimizar a expressão do quadrado dos resíduos,
∑r [i(ψ r ) – ir ]2 = F(α,ß)
Diferenciando em ordem aos parâmetros, resulta o sistema de equações,
∂F
= 2·∑ α ψr + β ψr2m+1 – ir · ψr = 0
∂α
r
∂F
∂β
= 2·∑
α ψr + β ψr2m+1 – ir · ψr2m+1 = 0
r
A este sistema de equações pode ser dada a forma:
∑r ψr2
∑r
·α +
ψr2m + 2
∑r ψr2m+1
·α +
∑r
·β =
2
ψr2m+2
∑r irψr
·β =
≡ [S]·{a} = {t}
∑r
irψr2m+1
A solução deste sistema de equações pode ser, rapidamente, determinada recorrendo à regra de Cramer. Com o
auxílio de um pequeno programa de computador, onde se considera que a amostragem foi feita em np pontos,
determina-se os valores dos parâmetros {α, ß} que ficarão no vector {a}.
– MVG.92 –