No instante t = , uma fonte sonora que gera um tom com freqüência

No instante t = 0 , uma fonte sonora que gera um tom com freqüência de 500 Hz é arremessada verticalmente do solo com
velocidade inicial de 40 m/s . Pede-se:
a) a maior e a menor freqüência do som ouvido por um observador estacionário situado muito próximo do local do
arremesso:
b) um esboço do gráfico da freqüência ouvida pelo observador em função do tempo após o lançamento para 0 < t < 10s .
Dados: aceleração da gravidade ( g ) = 10m/s 2 ;
velocidade do som ( vS ) = 340 m/s 2 .
Obs.: despreze o atrito da fonte sonora com o ar e suponha que a fonte permaneça imóvel após atingir o solo.
Resolução:
a)
A partícula é lançada com v f o = 40 m/s , e então, chega ao solo novamente com v f = −40 m/s : Assim;
i)
Maior freqüência:
Ocorre quando a aproximação for máxima, ou seja, instante em que a fonte retorna ao solo:
f = f0 ⋅
vS ± v0
⇒
vS ± v f
340
⇒
340 − 40
340
= 500 ⋅
= 567 Hz
300
f máx = f 0 ⋅
f máx
ii)
Menor freqüência:
Ocorre quando o afastamento for máximo, ou seja, instante de lançamento:
340
⇒
f mín = f 0 ⋅
340 + 40
f mín = 500 ⋅
b)
340
= 447 Hz
380
A freqüência do instante do lançamento até a queda pode ser determinada pela seguinte equação:
340
340
f = f0 ⋅
⇒ f = 500 ⋅
380 − 10t
340 + ( 40 − 10t )
Sendo que o lançamento dura 8s
(v
f
= −40m/s ) .
Após, a queda, a partícula está em repouso, e então a freqüência ouvida é constante.
Gráfico:
A figura ilustra um bloco M de madeira com formato cúbico, parcialmente submerso em água, ao qual está fixado um
cursor metálico conectado a um circuito elétrico. Na situação inicial, a face do fundo do bloco se encontra a 48cm da
superfície da água, a chave K está aberta e o capacitor C1 descarregado. O comprimento do fio resistivo entre a posição b
do cursor metálico e o ponto a é 10cm . A potência dissipada no resistor R1 é 16 W .
Em determinado instante, a água é substituída por outro líquido mais denso, mantendo-se constante o nível H da coluna de
água inicialmente existente. Fecha-se a chave K e observa-se que, após um longo intervalo de tempo, a energia armazenada
em C1 se estabiliza em 28,8 μ J . Considerando que a resistência por unidade de comprimento do fio resistivo é constante,
determine a massa específica do líquido que substituiu a água.
Dados: aceleração da gravidade ( g ) = 10m/s 2 ;
massa específica da água ( μ0 ) = 1 g / cm3 .
Resolução:
Substituindo o líquido por outro mais denso, para que o corpo permaneça em equilíbrio, o volume deslocado diminui, e logo, o bloco
sobe mudando a posição do cursor b . Assim:
i)
Na posição inicial:
Pela potência em R1 descobriremos U e i nesse resistor:
P = R ⋅ i 2 ⇒ 16 = 1 ⋅ i 2 ⇒ i = 4 A
U = R ⋅ i ⇒ U = 1⋅ 4 = 4 V
Então, no reostato temos,
U ab = 24 − 4 = 20 V
E por fim:
U = R ⋅ i ⇒ 20 = Rab ⋅ 4 ⇒
Rab = 5Ω
ii)
Na posição final:
Para o capacitor carregado:
CU 2
U2
E=
⇒ 28,8μ = 10μ ⋅
⇒
2
2
U = 2,4 V
E estando o capacitor em paralelo com R1 :
U C = R1 ⋅ i' ∴ i' = 2 ,4 A
que é a nova corrente.
Então para o cálculo da resistência final do reostato ( R'ab ) :
U 'ab = 24 − 2 , 4 = 21,6 V
Logo:
U 'ab = R'ab ⋅ i' ⇒ 21,6 = R'ab ⋅ 2,4 ⇒
R'ab = 9 Ω
Por fim, se a resistência por unidade de comprimento é constante, a resistência total é proporcional ao comprimento do fio:
Rab
:
R'ab
⇒
Lab
:
L'ab
5
9
=
⇒ L'ab = 18cm
10cm L'ab
Portanto, o cursor (e também o bloco) subiram 8cm , e como os empuxos no início e no fim equilibram a força peso no bloco:
E0 = E f
μ a ⋅ g ⋅ V0 = μ 2 ⋅ gV f
μc ⋅ g ⋅ A ⋅ 48 ⋅ 10−2 = μ L ⋅ g ⋅ A ⋅ 40 ⋅ 10−2
μ L = 1,2g/cm3
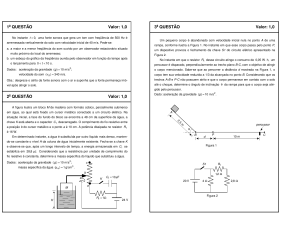
Um pequeno corpo é abandonado com velocidade inicial nula no ponto A de uma rampa, conforme ilustra a Figura 1 .
No instante em que esse corpo passa pelo ponto P , um dispositivo provoca o fechamento da chave S1 do circuito elétrico
apresentado na Figura 2 .
No instante em que o resistor R1 desse circuito atinge o consumo de 0,05 W ⋅ h um percussor é disparado, perpendicularmente
ao trecho plano BC , com o objetivo de atingir o corpo mencionado. Sabe-se que ao percorrer a distância d mostrada na
figura 1 , o corpo tem sua velocidade reduzida a 1 / 3 da alcançada no ponto B . Considerando que os trechos AB e PC não
possuem atrito e que o corpo permanece em contato com o solo até o choque, determine o ângulo de inclinação θ da
rampa para que o corpo seja atingido pelo percussor.
Dado: aceleração da gravidade ( g ) = 10 m / s 2 .
Resolução:
Cálculo do intervalo de tempo Δt entre o fechamento da chave S1 e o disparo do percussor.
4 i − 20 = 0
i =5A
P1 = R1 ⋅ i 2
P1 = 1,2 ⋅ 52 W
P1 = 30 W
P1 ⋅ Δt = E1
30 ⋅ Δt = 0 ,05 Wh
0 ,05
⋅ 3600s
30
Δt = 6s
Δt =
No trecho PC não temos atrito, então o corpo vai em movimento uniforme:
Seja v p o módulo da velocidade do corpo no ponto P .
vP =
Δs 10 m 5
=
= m/s (o bloco deve ser atingido pelo percussor)
Δt
6s
3
Seja o vB módulo da velocidade do corpo no ponto B .
1
5 1
vP = vB ⇒ = vB ⇒ vB = 5m/s .
3
3 3
Fazendo conservação de energia no trecho AB .
m vB2
mgh =
2
2
v
25
h= B =
2 g 2 ⋅ 10
h = 1, 25m
Voltando à figura:
1, 25 1
=
2 ,5 2
∴ θ = 30°
sen θ =
Uma mola com constante elástica k , presa somente a uma parede vertical, encontra-se inicialmente comprimida em
10cm por um bloco de massa m = 4 kg , conforme apresenta a figura abaixo. O bloco é liberado e percorre uma superfície
horizontal lisa AO sem atrito. Em seguida, o bloco percorre, até atingir o repouso, parte da superfície rugosa de uma viga
com 4 m de comprimento, feita de material uniforme e homogêneo, com o perfil mostrado na figura. Sabendo que a força
normal por unidade de área no tirante CD de seção reta 10mm 2 é de 15 MPa na posição de repouso do bloco sobre a viga,
determine o valor da constante elástica k da mola.
Dados: pesos por unidade de comprimento da viga ( PL1 ) = 20 N/m e ( PL 2 ) = 40 N/m ;
coeficiente de atrito cinético ( μC ) = 0,50 ;
aceleração da gravidade ( g ) = 10m/s 2 ;
1 Pa = 1N/m 2 .
Obs.: o tirante não prejudica o movimento do bloco.
Resolução:
Determinação da posição em que o bloco para sobre a viga:
∑M = 0
= P1 ⋅ 3 + N ⋅ x + P2 ⋅ 1 − F ⋅ 2 = 0
120 + 40 x + 80 − 300 = 0
x = 2 ,5m
Notemos que o bloco percorreu 1,5m sobre a viga até parar:
τ Fat = Δ Ec
Fat ⋅ d ⋅ cos180º = 0 −
μ ⋅ N ⋅ d ⋅ ( −1) = −
μ ⋅ mg ⋅ d =
mv 2
, em que v é a velocidade de chegada à viga.
2
mv 2
2
mv 2
2
v = 2 ⋅ μg ⋅ d
v = 2 ⋅ 0 ,5 ⋅ 10 ⋅ 1,5
v = 15 m/s
Antes da chegada á viga o sistema é conservatório:
kx 2 mv 2
=
2
2
2
mv
k= 2
x
k=
4⋅
( 15 )
2
(10 ⋅ 10−2 )
2
k = 6 ⋅ 103 N/m
=
4 ⋅ 15
10−2
A figura 1 ilustra uma bateria, modelada através de uma fonte de tensão elétrica VF em série com um resistor RS ,
conectada a um voltímetro V , cuja leitura indica 24 V . Essa bateria é ligada em série com o amperímetro A e com um
circuito composto por uma resistência de aquecimento RA em paralelo com uma resistência RB , conforme mostra a Figura
2 . A resistência RA encontra-se imersa em 0,2 L de um líquido com massa específica de 1,2 g / cm3 .
Inicialmente, as chaves S1 e S 2 da figura 2 encontram-se abertas. A chave S1 é acionada. Observa-se que o amperímetro
indica 2 A e que a temperatura do líquido se eleva a 10 °C para 40 °C em 30 minutos. Em seguida, a chave S 2 é fechada e
o amperímetro passa a indicar 2 ,4 A . Considerando que não exista perda de energia no aquecimento da água e que o
voltímetro e o amperímetro sejam ideais, determine:
a) a resistência RA em ohms;
b) a resistência RS em ohms;
c) a resistência RB em ohms.
Dados: calor específico do líquido ( c ) = 2cal/ ( g°C ) ;
1cal ≅ 4 J .
Resolução:
a)
Calculo da potência dissipada em RA :
m ⋅ c ⋅ Δθ d ⋅ V ⋅ c ⋅ Δθ
=
Δt
Δt
g
cal
⋅ 30º C
1,2 3 ⋅ 200cm3 ⋅ 2
J
cal
cm
gº C
PA =
=8
= 8,4
30 ⋅ 60 ⋅ s
s
s
PA = 32 W
PA =
Q
Δt
=
Lembrando que PA = RA ⋅ i 2 vem:
PA 32 W
=
i 2 2 2 A2
RA = 8Ω
RA =
b)
Como VF = 24 V (situação da figura 1 ):
VF = RS ⋅ i + RA ⋅ i
RS =
VF
24V
− RA =
− 8Ω = 12Ω − 8Ω
i
2A
RS = 4Ω
c)
Com as chaves S1 e S 2 fechadas:
+4 ⋅ 2 ,4 + 8 ⋅ i − 24 = 0
i = 1,8A
+ RB ⋅ ( 2 ,4 − i ) − 8 ⋅ i = 0
RB ⋅ 0 ,6 − 8 ⋅ 1,8 = 0
RB = 24Ω
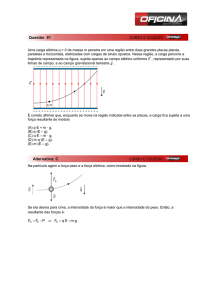
Uma massa m de ar, inicialmente a uma pressão de 3atm , ocupa 0,1m3 em um balão. Este gás é expandido
isobaricamente até um volume de 0,2m3 e, em seguida, ocorre uma nova expansão através de um processo isotérmico,
sendo o trabalho realizado pelo gás durante esta última expansão igual a 66000 J . Determine:
a) o trabalho total realizado em joules pelo gás durante todo o processo de expansão;
b) o calor total associado às duas expansões, interpretando fisicamente o sinal desta grandeza.
Dados: 1atm = 1
Cp
kgf
= 14.
, 1 kgf = 10 N e γ =
2
Cv
cm
Obs.: Suponha que o ar nestas condições possa ser considerado como gás ideal.
Resolução:
a)
Na transformação isobárica:
τ 1 = p ⋅ ΔV = 3 ⋅ 105 ⋅ ( 0 ,2 − 0 ,1 ) = 3 ⋅ 104 J
o trabalho na transformação isotérmica foi fornecido:
τ 2 = 66000J
Logo,
τ T = τ 1 + τ 2 = 66000 + 30000
τ T = 96000J
b)
Na transformação isobárica temos:
Q1 = n ⋅ C p ⋅ ΔT , onde:
C p − Cv = R ⇒ C p −
⎛ 1⎞
R ⋅γ
= R ⇒ C p ⎜1 − ⎟ = R ⇒ C p =
γ
γ −1
⎝ γ⎠
Cp
Assim:
R ⋅γ
γ
⋅ ΔT =
⋅ n ⋅ R ⋅ ΔT ⇒
γ −1
γ −1
γ
γ
1, 4
Q1 =
= p ⋅ ΔV =
⋅τ1 =
⋅ 30000 ⇒
1, 4 − 1
γ −1
γ −1
Q1 = n
Q1 = 105000 J
Na transformação isotérmica:
Q2 = τ 2 + ΔU , em que ΔU = 0 , por tanto:
Q2 = τ 2 = 66000J
Por fim o calor total será:
QT = Q1 + Q2 = 105000 + 66000 = 171000 J.
Concluímos que, sendo positiva essa grandeza, o calor é recebido pelo gás durante as transformações.
Um pêndulo com comprimento L = 1m , inicialmente em repouso, sustenta uma partícula com massa m = 1kg . Uma
segunda partícula com massa m = 1kg movimenta-se na direção horizontal com velocidade constante v0 até realizar um
choque perfeitamente inelástico com a primeira. Em função do choque, o pêndulo entra em movimento e atinge um
obstáculo, conforme ilustrado na figura. Observa-se que a maior altura alcançada pela partícula sustentada pelo pêndulo é
a mesma do ponto inferior do obstáculo. O fio pendular possui massa desprezível e permanece sempre esticado.
Considerando a aceleração da gravidade g = 10 m/s 2 e a resistência do ar desprezível, determine:
a) a velocidade v0 da partícula com massa M antes do choque;
b) a força que o fio exerce sobre a partícula de massa m imediatamente após o fio bater no obstáculo.
Resolução:
a)
Após a colisão o sistema é conservativo:
2m ⋅ v 2
= 2m ⋅ g ⋅ 0,8 L , em que v é o módulo da velocidade do conjunto imediatamente após a colisão:
2
v 2 = 1,6 ⋅ g ⋅ L = 1,6 ⋅ 10 ⋅ 1
v = 4 m/s
Na colisão temos conservação da quantidade de movimento:
m ⋅ v0 = 2m ⋅ v
JJG
v0 = 8m/s (a direção e o sentido do v0 estão indicados na figura do enunciado da questão).
b)
Cálculo de v' :
L
2m ⋅ v 2 2m ⋅ v' 2
=
+ 2m ⋅ g ⋅
2
2
2
v' 2
8=
+5
2
v' 2 = 6 m 2 /s 2
Lembrando que agora o raio da curva é 0,6 L :
T − 2mg ⋅ cos 60° =
T − mg =
2m ⋅ v' 2
0 ,6 L
m ⋅ v' 2
0 ,3L
m ⋅ v' 2
1⋅ 6
= 1 ⋅ 10 +
0 ,3L
0,3 ⋅ 1
T = 30 N , que é a intensidade da força que o fio exerce sobre a partícula, lembrando que ela atua na direção do fio conforme
T = mg +
indicado na figura.
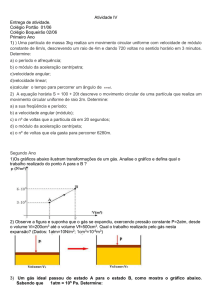
Uma partícula de massa m e carga elétrica q é arremessada com velocidade escalar v numa região entre duas placas
JG
de comprimento d , onde existe um campo elétrico uniforme E, conforme ilustra a figura. Ao sair da região entre as placas,
JG
a partícula entra numa região sujeita a um campo magnético uniforme B e segue uma trajetória igual uma semicircunferência, retornando à região entre as placas. Pede-se:
a) o ângulo θ de arremesso da partícula indicado na figura;
b) a energia cinética da partícula no instante de sue retorno à região entre as placas;
JG
c) a faixa de valores de B para que a partícula volte à região entre as placas;
d)
verificar, justificando, se existe a certeza da partícula se chocar com alguma das placas após regressar à região entre as
placas.
Obs.: desconsidere a ação da gravidade.
Resolução:
a)
JG
Para que a partícula faça uma semi-circunferência na região de B , ela deve sair da região entre as placas na direção horizontal
JG
( q > 0 ) , assim; ao término da travessia do campo E teremos v y = 0 :
FR = q ⋅ E = m ⋅ a y ⇒ a y =
qE
m
E para as velocidades:
v y = voy − a y t ⇒ 0 = v ⋅ sen θ −
qE
⋅t
m
( I)
Sendo que no eixo x:
d
d = vx ⋅ t ⇒ t =
( II )
v ⋅ cosθ
Substituindo ( II ) em ( I ) :
0 = v sen θ −
θ=
b)
qE
d
Ed
⋅
⇒ sen 2θ = 2q 2
m v cos θ
mv
1
⎛ 2qEd ⎞
⋅ arcsen ⎜
2 ⎟
2
⎝ mv ⎠
A carga retorna às placas com a mesma energia com que saiu já que o campo magnético não realiza trabalho.
mvx2 mv 2 ⋅ cos 2 θ
EC =
=
( III )
2
2
Calculo de cos 2 θ :
cos 2 2θ = 1 − sen 2 2θ
cos 2θ= 1 − sen 2 2θ
2cos 2θ − 1 = 1 − sen 2 2θ
cos 2 θ =
1 + 1 − sen 2 2θ
2
⎛ 2qEd ⎞
1+ 1− ⎜
2 ⎟
⎝ mv ⎠
2
cos θ=
2
Voltando em ( III ) :
2
2
⎛
⎞ ⎞⎟
⎜1 + 1 − ⎛⎜ 2qEd
⎟
2
2 ⎞
⎝ mv ⎠ ⎟ mv 2 ⎛
mv 2 ⎜⎝
⎠=
⎜1 + 1 − ⎛⎜ 2qEd ⎞⎟ ⎟
⋅
EC =
2
2
2
4 ⎜
⎝ mv ⎠ ⎟
⎝
⎠
c)
Cálculo do afastamento H da carga à placa negativa no instante em que ela entra na região do campo magnético.
1
1 qE
d2
H = at 2 = ⋅
⋅ 2
2
2 m v cos 2 θ
qEd 2
H=
2
⎛
⎛ 2qEd ⎞ ⎞⎟
mv 2 ⋅ ⎜1 + 1 − ⎜
2 ⎟
⎜
⎝ mv ⎠ ⎟⎠
⎝
Analisando o MCU na região do campo magnético:
mvx2
mv
qvx ⋅ B =
⇒R= x
R
qB
R=
mv ⋅ cos θ
.
qB
Observe na figura que R <
H
2
mv ⋅ cos θ H
<
2
qB
B>
2mv ⋅ cos θ
q⋅H
Substituindo H e cos θ vem:
3
2 ⎤2
4m v ⎡ 1 ⎛
⎛ 2qEd ⎞ ⎞⎟ ⎥
B > 2 2 ⎢ ⎜1 + 1 − ⎜
2 ⎟
q Ed ⎢ 2 ⎜
⎝ mv ⎠ ⎟⎠ ⎥
⎣ ⎝
⎦
2 3
d)
Ao voltar para a região entre as placas, a partícula será lançada horizontalmente com velocidade v X e durante a travessia terá um
deslocamento H para cima em y .
Assim, ao retornar às placas, a carga se choca certamente com a placa superior.
Um explorador espacial sofreu um acidente e encontra-se em um planeta desconhecido. Entre seus equipamentos, ele
dispõe de um telescópio, um dinamômetro, um bloco de massa M conhecida e um fio de comprimento L . O telescópio é
composto por uma objetiva e uma ocular com distâncias focais f e f ' , respectivamente. O explorador observou a
existência de um satélite no céu deste planeta e o telescópio apresentou uma imagem de diâmetro máximo 2r' . Medidas
anteriores ao acidente indicavam que o raio deste satélite era, na realidade, R . O astronauta determinou que o período de
revolução do satélite em torno do planeta era equivalente a 5000 períodos de um pêndulo improvisado com o bloco e o fio.
Se o dinamômetro registra que este bloco causa uma força F sob efeito da gravidade na superfície do planeta, determine:
a) a massa M em função dos parâmetros fornecidos;
b) o diâmetro D deste planeta em função dos parâmetros fornecidos.
Dado: constante da gravitação universal = G .
Resolução:
a)
Como descreve o enunciado, a massa M do bloco é conhecida. Então, neste item a banca examinadora provavelmente gostaria de
ter pedido a massa do planeta M P .
Da indicação do dinamômetro:
F
F = M ⋅ g0 ⇒ g0 =
M
Para o pêndulo simples
L
LM
= 2π
t = 2π
g0
F
Usando agora a órbita do satélite
Fcp = FG
2
G ⋅ MS ⋅ MP
d3
⎛ 2π ⎞
⇒ T = 2π
MS ⋅⎜
⎟ ⋅d =
2
d
GM P
⎝ T ⎠
Como T = 5000 ⋅ t vem
2π
d3
LM
= 5000 ⋅ 2π
GM P
F
F ⋅ d3
, sendo d a distância até o satélite.
25 ⋅ 106 L ⋅ M ⋅ G
Para a determinação de d , consideraremos que a distância da superfície do planeta ao satélite é aproximadamente igual a distância
entre os centros de massa do planeta e do satélite. Assim, d é a distância medida do satélite ao objetiva do telescópio conforme a
figura abaixo
MP =
Por semelhança de triângulos
r R
=
f d
f ⋅R
( I)
d
Lembrando que a imagem da primeira lente é objeto para a segunda e que a segunda imagem deve ser formada a 0 ,25m da ocular
r=
1 1
1
= +
f ' p −0 ,25
( II )
r' − p' 0 ,25
=
=
r
p
p
( III )
De ( I ) e ( III ) :
r' ⋅ d 0 ,25
1 4r' d
=
, que substituindo em ( II ) conduz a:
=
⇒
p f ⋅R
f ⋅R
p
1 4r' d
( 4 f ' + 1) f ⋅ R .
=
−4 ⇒ d =
f' f ⋅R
4r'
⎡ ( 4 f ' + 1) f ⋅ R ⎤
F
⎢
⎥ .
25 ⋅ 106 L ⋅ M ⋅ G ⎣
4r'
⎦
3
Do exposto concluímos M P =
b)
g0 =
GM P
RP2
F GM P
=
M
RP2
GM
GM
F ⋅ d3
⋅ MP =
⋅
F
F 25 ⋅ 106 L ⋅ M ⋅ G
d3
RP2 =
25 ⋅ 106 L
RP2 =
3
d 2
5 ⋅ 103 L
Substituindo d
RP =
RP =
1
4 ⋅ 104 L
⎡ ( 4 f ' + 1) f ⋅ R ⎤
⋅⎢
⎥
r'
⎣
⎦
3
2
3
∴ D = 2 RP =
⎡ ( 4 f ' + 1) f ⋅ R ⎤ 2
1
⋅⎢
⎥ .
4
r'
2 ⋅ 10 L ⎣
⎦
A figura ilustra uma empacotadora de papel que utiliza um capacitor de placas quadradas e paralelas para empilhar a
quantidade exata de folhas contidas em cada embalagem. Ao atingir a altura limite do bloco de papel, o laser L acoplado
à fenda simples F5 projeta os mínimos de intensidade de difração de primeira ordem nos pontos A e B , eqüidistantes da
linha tracejada ED . Sabendo que cada folha de papel possui uma espessura e f . Determine o número de folhas contidas em
cada embalagem.
Dados: comprimento de onda do laser = λ ;
largura da fenda simples = a ;
distância entre a fenda e a reta AB = 2d ;
área da superfície das placas do capacitor = d 2 ;
permissividade do vácuo = ε 0 ;
permissividade do papel = ε ;
capacitância do capacitor com o limite máximo de folhas de papel = C .
Obs.: despreze o efeito da borda do capacitor.
Resolução:
Com o limite máximo de folhas, podemos escrever para o capacitor:
C ⋅C
ε⋅d2
ε ⋅d2
e CBC =
C = AB BC ( I ) , onde C AB = 0
C AB + CBC
x
N ⋅ ef
Onde x pode ser determinado pela difração na fenda simples:
i)
a sen θ = m ⋅ λ (com m = 1 )
⇒ sen θ =
ii)
sen θ =
λ
a
x
2
2
⎛ x⎞
2
⎜ ⎟ + ( 2d )
⎝2⎠
De i) e ii):
x
λ
λ2
x2
2
=
⇒4 2 = 2
⇒
2
x
a
a
2
⎛x⎞
2
+ 4d
⎜ ⎟ + ( 2d )
4
⎝2⎠
x2
a2
+ 4d 2 = x 2 ⋅ 2 ⇒
4
4λ
⎛ a2
⎞
⋅ ⎜ 2 − 1⎟ = 4 d 2 ⇒
λ
⎝
⎠
4d
x=
a2
−1
λ2
x2
4
E por fim, resolvendo
C=
C=
( I) :
C AB ⋅ CBC
⇒
C AB + CBC
ε 0 d 2 εd 2
⋅
x N ⋅ ef
ε0d 2
εd 2
+
x
N ⋅ ef
⇒
⎛ N ⋅ e f ⋅ ε0 ⋅ d 2 + xε ⋅ d 2 ⎞ ε ⋅ ε 0 ⋅ d 4
C⎜
⇒
⎟⎟ =
⎜
x ⋅ N ⋅ ef
⎝
⎠ x ⋅ N ⋅ ef
ε ⋅ ε0 ⋅ d 4
− x⋅ε⋅d2
C
⎛ ε⋅d2
ε⎞ 1
N =⎜
− x ⎟⋅
C
ε
0 ⎠ ef
⎝
4d
Sendo x =
⇒
a2
−1
λ2
N ⋅ e f ⋅ ε0 ⋅ d 2 =
⎛
⎞
⎜
⎟
2
1 ε⋅d
4d ⋅ ε ⎟
N = ⋅⎜
−
⎟
ef ⎜ C
a2
⎜
−1 ⎟
2
λ
⎝
⎠
Obs: Não consideramos θ pequeno já que para isso seria preciso a bem maior que λ , o que não é estriamente necessário.