2 Semestre – 2008 Exame de Conhecimento em Física

UNIVERSIDADE FEDERAL DE GOIAS
INSTITUTO DE FÍSICA
C.P. 131, CEP 74001-970, Goiânia - Goiás - Brazil.
Fone/Fax: +55 62 521-1029
Programa de Pós-Graduação
Processo de Seleção – 20 Semestre – 2008
Exame de Conhecimento em Física
Nome:___________________________________________________ Data: 28/07/2008
1) É dada a onda eletromagnética
, onde E0
é uma constante. Quais são respectivamente o campo magnético
(A)
e o vetor de Poynting:
e
(B)
e
(C)
e
(D)
e
(E)
e
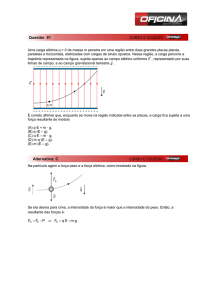
2) Uma antena em forma de espira de área A e resistência R é perpendicular a um campo
magnético uniforme B. O campo cai linearmente a zero em um intervalo de tempo t.
Encontre uma expressão para a energia total interna dissipada por efeito Joule na espira.
(A)
=
,
(B)
=
,
(C)
=
,
(D)
=
,
(E) n.d.a.
3) Enquanto um capacitor de placas paralelas circulares, de diâmetro 20 cm, está sendo
carregado, a densidade de corrente de deslocamento através da região entre as placas é
uniforme e tem módulo igual a 20 A/m2. Quais são respectivamente o módulo do campo
magnético B numa distância r = 50 mm do eixo de simetria da região e a variação do
campo elétrico com relação ao tempo, dE/dt, nesta mesma região.
(A) 2,3 x 1010 V/m.s
(B) 2,3 x 1010 mV/m.s
(C) 2,3 x 1011 V/m.s
(D) 2,3 x 1011 mV/m.s
(E) n.d.a.
4) Um capacitor de duas placas circulares de raio R = 18,0 cm está ligado a uma fonte de
fem
, onde
= 220 V e = 130 rad/s. O Valor máximo da corrente de
deslocamento é
= 7,60 µA. Despreze a distorção do campo elétrico nas bordas das
placas. Qual o valor máximo de
, onde F E é o fluxo elétrico na região entre as
placas?
(A) 859 V.m/s
(B) 859 mV.m/s
(C) 859 MV.m/s
(D) 859 kV.m/s
(E) n.d.a.
5) Na máquina térmica abaixo existe um problema, identifique-o:
(A) viola a primeira lei da termodinâmica;
(B) viola a segunda lei da termodinâmica;
(C) viola a terceira lei da termodinâmica;
(D) nada está errado.
(E) n.d.a.
1
6) A entropia de um fluido é dada por: s=A UVN 3 , onde A é uma constante. Qual das
expressões abaixo representa a energia interna U(S,V,N) do fluido:
(A) U=
,
(B) U=
,
(C) U=
,
(D) U=
,
(E) n.d.a.
7) Qual das afirmações abaixo está correta?
(A) para uma reação exotérmica em recipiente fechado e indeformável, U > 0.
(B) para uma reação endotérmica em recipiente fechado que ocorra aumento de volume
U é sempre positivo.
(C) se considerarmos um sistema e o meio exterior globalmente isolados, então Usist +
Uext = 0.
(D) Num sistema fechado, não há trocas de energia, sob a forma de calor, com o exterior.
(E) nenhuma da afirmações acima está correta.
8) Um recipiente de paredes adiabáticas contém 2 litros de água a 30 oC. Coloca-se nele um
bloco de 500g de gelo. De quanto variou a entropia no universo?
(A) 1,02 cal/K.
(B) 1,20 cal/K.
(C)10,2 cal/K.
(D) 12,0 cal/K.
(E)120,0 cal/K.
9) Considere um sistema de massa m com uma única coordenada generalizada q e
Lagrangena
, onde b e k são constantes positivas. Qual das
expressões abaixo pode representar uma das possíveis equações de movimento deste
sistema?
(A)
.
(B)
.
(C)
.
(D)
.
(E)
10) Sobre uma partícula, atua uma força do tipo
. Calcule o trabalho dessa
força entre os pontos (0,0) e (1,1); nos caminhos: a) y = x; b) y = x2. Por fim, verifique se
essa força é conservativa.
(A)
,
(B)
,
(C)
,
(D)
,
, força não-conservativa.
, força não-conservativa.
, força conservativa.
, força conservativa.
(E) nenhuma das respostas.
11) Um satélite de massa m e energia total E ocupa uma órbita circular de raio R ao redor da
Terra. Num certo ponto da órbita, o satélite é acelerado para ocupar uma órbita elíptica,
no mesmo plano da anterior e com a Terra em um dos focos. A elipse possui perigeo R e
apogeo 2R. Quais são os valores das velocidades do satélite antes, Va, e depois, Vb, de
acelerar? Qual é a variação de energia cinética desse processo? Qual será a velocidade,
Vap, do satélite na posição do apogeo?
(A)
,
,
,
;
(B)
,
,
,
;
(C)
,
,
,
;
(D)
,
,
,
;
(E) nenhuma das respostas.
12) Uma molécula de amônia NH3 pode ser estudada considerando um sistema de dois níveis.
A molécula forma uma pirâmide, onde os três átomos de hidrogênio estão na base da
pirâmide formando um triângulo, e o átomo de nitrogênio está localizado no topo da
pirâmide. Os dois estados correspondem ao átomo de nitrogênio colocado acima ou
abaixo do plano definido pelos átomos de hidrogênio, ou seja, os estados
,
acima do plano, e
, abaixo do plano. Nesta base a Hamiltoniana do sistema
é dada por:
,
onde A é uma constante. Se a molécula está no estado
de encontrá-la no estado
em t > 0?
(A) 1/2.
(B) 1/4.
(C)
.
(D)
.
(E)
.
em t = 0, qual a probabilidade
13) Uma partícula está no estado fundamental de um potencial unidimensional de
comprimento L, ou seja, V(x) é diferente de zero somente entre -L/2 < x < L/2.
Subitamente o potencial que confina a partícula é modificado expandindo simetricamente
em ambas as direções para duas vezes o comprimento original 2L (agora V(x) é diferente
de zero somente entre -L < x < L), sem qualquer mudança no estado da partícula.
Determine a probabilidade de encontrar a partícula no estado fundamental no novo
potencial de confinamento.
(A)
.
(B)
(C) 1/2.
.
(D)
(E) 1/4.
.
14) O operador Hamiltoniano para um sistema de dois estados
e
é dado por
onde a é um número com dimensão de energia.
Encontre os autovalores de H e os correspondentes autovetores
e
(como uma
combinação linear de
e ).
(A)
e
;
(B)
e
;
(C)
e
;
(D)
e
(E)
e
e
.
e
e
;
.
e
;
.
.
e
.