SOH CAH TOA

Módulo 8 - Trigonometria
Trigonometria
Trigonometria
HIP
CAT1
CAT2
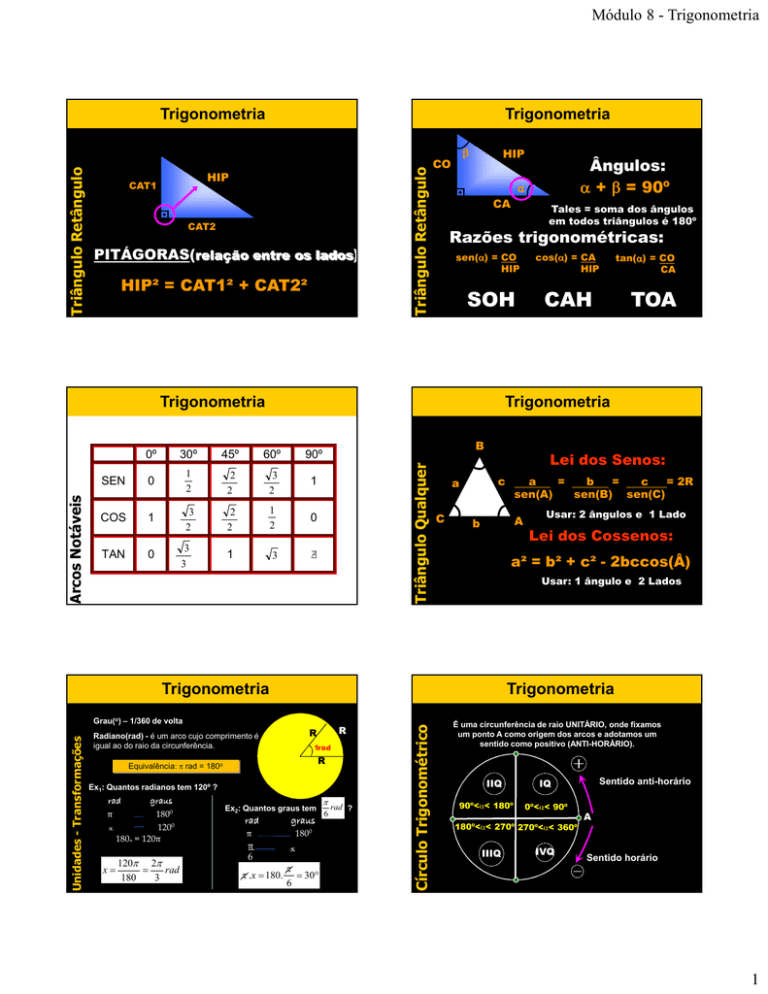
PITÁGORAS(relação entre os lados)
HIP² = CAT1² + CAT2²
Triângulo Retângulo
Triângulo Retângulo
β
HIP
CO
α
CA
sen(α
α) = CO
HIP
SOH
45º
60º
90º
SEN
0
1
2
2
2
3
2
1
COS
1
3
2
2
2
1
2
0
1
3
∃
C
1rad
..
180o
R
Ex1: Quantos radianos tem 120º ?
x
120π 2π
x=
=
rad
180
3
Ex2: Quantos graus tem
rad
graus
1800
π
π
6
π .x = 180.
x
π
6
= 30°
π
6
rad ?
Círculo Trigonométrico
Unidades - Transformações
R
R
Radiano(rad) - é um arco cujo comprimento é
igual ao do raio da circunferência.
graus
1800
1200
180x = 120π
a
=
b
=
c
= 2R
sen(A)
sen(B) sen(C)
c
a
A
b
Usar: 2 ângulos e 1 Lado
Lei dos Cossenos:
a² = b² + c² - 2bccos(Â)
Usar: 1 ângulo e 2 Lados
Trigonometria
Grau(o) – 1/360 de volta
rad
π
TOA
CAH
Lei dos Senos:
Trigonometria
Equivalência: π rad =
tan(α
α) = CO
CA
B
Triângulo Qualquer
Arcos Notáveis
30º
0
cos(α
α) = CA
HIP
Trigonometria
0º
TAN
Tales = soma dos ângulos
em todos triângulos é 180º
Razões trigonométricas:
Trigonometria
3
3
Ângulos:
α + β = 90º
É uma circunferência de raio UNITÁRIO, onde fixamos
um ponto A como origem dos arcos e adotamos um
sentido como positivo (ANTI-HORÁRIO).
IIQ
90º<α< 180º
Sentido anti-horário
IQ
0º<α< 90º
A
180º<α< 270º 270º<α< 360º
IIIQ
IVQ
Sentido horário
1
Módulo 8 - Trigonometria
Trigonometria
Função
Razão
IQ
IIQ
IIIQ
IVQ
Inversa
sen
+
+
-
-
csc
cos
+
-
-
+
sec
tan
+
-
+
-
cot
Divisas dos Quadrantes
Tabela dos Sinais
Trigonometria
0º
0
1
0
sen
cos
tan
cot
sec
csc
1
∃
∃
1
• Forma geral:
2070º
x = α + 2πk ou x = α + 360ºk
Procedimento: Se for > 360º:
÷ 360 e pegar o resto(1ª. DP)
Ângulos Simétricos
Falta
Tabela
Passa
Falta
180º
360º
IQ
30º
45º
60º
II Q
150º
135º
120º
III Q
210º
225º
240º
IV Q
330º
315º
300º
Simétricos
Trigonometria
Trigonometria
Caso 1: Ângulo é do IQ
Caso 2: Ângulo é do IIQ,IIIQ,IVQ
• Da tabela(30º, 45º, 60º) ou
• Usar ângulos simétricos ou FPF, após
• Será dado se for ≠
• Tabela dos Sinais
Imediatas:
• Voltar para o caso 1
Caso 3: Ângulo é uma divisa(0º, 90º,180º,270º,360º)
• Construir círculos ou usar a tabela das divisas
0º
30º
45º
60º
90º
SEN
0
1
2
2
2
3
2
1
COS
1
3
2
2
2
1
2
0
TAN
0
3
3
1
3
∃/
Obs:Nas inversas(cot,sec,csc)
COT
∃/
3
1
3
3
0
Usar tabela completa →
SEC
1
2 3
3
2
2
∃/
ou inverter a fração e racionalizar.
CSC
∃/
2
2
2 3
3
1
• Dividir por 360º e usar o resto(1ª DP)
Equações Trigonométricas
Valores – Casos 1,2,3 e 4
0
• São arcos que têm uma representação de mesmo tamanho
no círculo(mesmo valor) em um quadrante diferente. Deve-se
observar a tabela de sinais.
Ângulos Simétricos
Arcos Côngruos
• A diferença entre dois arcos
côngruos é sempre um
múltiplo de 360º(2π).
• Voltar para o caso 3 ou 2 ou 1
∃
Trigonometria
• São arcos que têm mesma
origem e mesma
extremidade.
Caso 4: Ângulo é maior que 360º
∃
180º 270º 360º
0
-1
0
-1
0
1
0
0
∃
0
∃
∃
-1
1
∃
-1
∃
∃
Os valores são obtidos pela construção do círculo
Trigonometria
690º
90º
1
0
sen x = número ou cos x = número ou tan x = número
cot x = número ou sec x = número ou csc x = número
Passos para Resolução:
Olhar o(s) ângulo(s)
correspondente(s) e pular para o
passo IV
I)O Valor está na tabela das
divisas?
Procurar o valor(sem sinal) na
tabela dos valores notáveis e
olhar o ângulo correspondente.
Este será o α.
II) Olhar o sinal para descobrir em quais quadrantes pertencem as respostas.
III) Se tiver resposta no IQ será o próprio α . Se for de outro quadrante: FPF.
IV) Escrever a expressão dos arcos côngruos: X = α + k.360º
V) Se necessário achar as respostas no intervalo pedido.
2
Módulo 8 - Trigonometria
Trigonometria
sen 2θ + cos 2 θ = 1
tan θ =
senθ
cos θ
cot θ =
cos θ
senθ
co
α
ca
Relações
1
csc θ =
senθ
hip ² = co ² + ca ²
sen =
1
sec θ =
cos θ
2
hip
co
ca
co
cos =
tan =
hip
hip
ca
hip
hip
ca
csc =
sec =
cot =
co
ca
co
2
csc θ = 1 + cot θ
sec 2 θ = tan 2 θ + 1
sen(a±b) = sen(a).cos(b) ± sen(b).cos(a)
Operações com Arcos
Por Triângulo
Trigonometria
cos(a±b) = cos(a).cos(b) ± sen(a).sen(b)
Ex1)Qual é o valor de sen 105º?
sen105º=sen(45º+60º)=sen45º.cos60º+sen60º.cos45º
2
2
sen (5π ) = sen (5.180°)
sen (900°) = sen180° = 0
2
2
f(x)= cos (x)
f(x)=y
0º(0 rad)
f(0º) = cos 0º = 0
1
90º(π/2 rad)
f(90º) = cos 90º = 1
0
180º(π rad)
f(180º) = cos 180º = 0
-1
+
1
. =
2
2
2
f(x)= sen (x)
f(x)=y
0º(0 rad)
f(0º) = sen 0º = 0
0
90º(π/2 rad)
f(90º) = sen 90º = 1
1
180º(π rad)
f(180º) = sen 180º = 0
0
270º(3π/2 rad)
f(270º) = sen 270º = -1
-1
6
2
+
4
4
y=f(x)=sen (x)= senóide
1
3π
π/2
2π
π
4π
π
π
π/2
0
x( ângulo)
-1
Período = 360º(2π
π)
Imagem = [-1, 1]
270º(3π/2 rad)
f(270º) = cos 270º = -1
0
y (valor)
y=f(x)=cos (x)= cossenóide
1
4π
π
2π
π
x( ângulo)
-1
Imagem = [-1, 1]
f(x) = cos(x)
π/2
Funções - Cosseno
Funções - Cosseno
2
6
+
4
4
Trigonometria
x(ângulo)
Período = 360º(2π
π)
3
2
.
x(ângulo)
Trigonometria
3π
π/2
2
=
2
y (valor)
Funções - Seno
Funções Trigonométricas
s (t ) = 10 +
π
.
Trigonometria
Suponha que o deslocamento de uma partícula sobre uma corda
vibrante seja dado pela equação s(t) = 10 + 1/4sen(10π t), em que t é o
tempo, em segundos, após iniciado o movimento, e s, medido em
centímetros, indica a posição. Meio segundo após iniciado o movimento
da corda, qual é, em cm, o afastamento da partícula da posição de
repouso?
a) 0 b) 0,125 c) 0,25 d) 10 e) 10,25
π/2
3
2
+
cos15º=cos(45º-30º)=cos45º.cos30º+sen45º.sen30º
• Aplicações
0
1
2
Ex2)Qual é o valor de cos 15º?
Trigonometria
1
sen(10π t )
4
1
s (0,5) = 10 + sen(10.π .0,5)
4
1
s (0,5) = 10 + sen(5π )
4
1
s (0,5) = 10 + .0 = 10
4
.
π
0
2π
π
Período = 2π
π
Imagem = [-1, 1]
y
1
3π
π/2
x
0
π/2
π
3π
π/2
2π
π
cos
1
0
-1
0
1
3π
π/2
0
π/2
π
2π
π
x
-1
3
Módulo 8 - Trigonometria
Trigonometria
Funções – Parâmetros
f(x) = A + B•sen(Cx + D)
f(x) = A + B•cos(Cx + D)
A= Modifica o Nível Médio(Muda a imagem-Translação):
A+ sobe A unidades e A– desce A unidades
B= Modifica a Amplitude(Muda a imagem-Variação):
B inteiro estica b vezes e B fração encolhe B vezes
C= Modifica o Período(P= 2π/C ou P= 360º/C):
C inteiro encolhe o período e C fração estica o período
D= Desloca Horizontalmente(Translação Horizontal):
D + vai para a esquerda e D – vai para a direita
4