Capítulo 1.

ESCOLA SUPERIOR DE TECNOLOGIA DE VISEU
DEPARTAMENTO DE MATEMÁTICA
Engenharia de Ambiente
Apontamentos da disciplina de
Complementos de Análise Matemática
Isabel Duarte
Ano lectivo 2005/2006
1. Elementos de Análise Vectorial
1
1.1. Campos vectoriais
Vamos estudar funções que a cada ponto P do plano ou do espaço associa um vector. Estas
funções chamam-se campos vectoriais. As suas principais aplicações envolvem campos de
velocidades, tais como correntes marítimas e velocidades do vento, e campos de forças,
como por exemplo o campo de forças gravitacional.
De entre os campos vectoriais, uns dos mais importantes são os conservativos, isto é,
aqueles em que há conservação de energia (a soma da energia cinética com a energia
potencial é constante), como é o caso do campo gravitacional e do campo magnético.
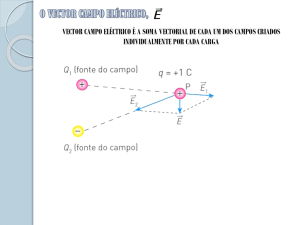
Os campos gravitacionais são definidos através da lei gravitacional de Newton
F ( x, y, z ) =
− Gm1m2
x2 + y2 + z2
u,
sendo G a constante de gravidade, m1 e m2 as massas das partículas localizadas em (x,y,z)
e (0,0,0) e u o vector unitário que vai desde (0,0,0) a (x,y,z).
Os campos de forças eléctricas são definidos através da lei de Coulomb
F ( x, y, z ) =
cq1q2
r
2
u,
sendo q1 e q2 as cargas eléctricas das partículas localizadas em (x,y,z) e (0,0,0), u o vector
unitário que vai desde (0,0,0) a (x,y,z) e c uma constante.
Estes dois campos são definidos do mesmo modo, F ( x, y, z ) =
k
r
2
u=
k
r
2
r
k
=
r.
3
r
r
Todos os campos assim definidos chamam-se campos quadrado inverso.
Na figura seguinte está representado um campo vectorial de uma roda a girar em torno de
um eixo.
1. Elementos de Análise Vectorial
2
Definição: Sejam M e N funções de x e y definidas numa região R do plano. A função
dada por
F(x,y)=M(x,y)i+N(x,y)j
chama-se campo vectorial sobre R.
Sejam M, N e P funções de x, y e z definidas numa região Q do espaço. A função dada por
F(x,y,z)=M(x,y,z)i+N(x,y,z)j+P(x,y,z)k
chama-se campo vectorial sobre Q.
Exemplo 1: Descrição do campo vectorial F sendo F(x,y)=
(
xi + yj
2
10 x + y
2
)
Exemplo 2: Descrição do campo vectorial F sendo F(x,y,z)=xi+yj+zk
3
.
2
1. Elementos de Análise Vectorial
3
O gradiente de uma função f, sendo dado por
(
grad f ( x, y, z ) = ∇f ( x, y, z ) = f x ( x, y, z ), f y ( x, y, z ), f z ( x, y, z )
)
ou
∇f ( x, y, z ) = f x ( x, y, z )i + f y ( x, y, z ) j + f z ( x, y, z )k
é um exemplo de um campo vectorial.
Exemplo 3: Descrição do campo vectorial gradiente de f(x,y)=x+y.
∇f ( x, y ) = 1i + ij
Definição: Um campo vectorial F é conservativo numa região se for o campo vectorial de
alguma função f naquela região, isto é, se existir uma função diferenciável f tal que F=∇f.
A função f chama-se função potencial de F na região.
Exemplo: Um campo quadrado inverso é conservativo em qualquer região que não
contenha a origem. A função f ( x, y ) = −
vectorial F ( x, y ) =
(x
c
2
+y
2
)
3
(x
c
2
+y
2
)
1
é a função potencial do campo
2
(xi + yj ) .
2
Podemos utilizar uma condição necessária e suficiente para mais facilmente ver se um
campo vectorial é conservativo.
1. Elementos de Análise Vectorial
4
Teorema: Se M e N tiverem derivadas parciais de primeira ordem contínuas numa bola
aberta R, o campo vectorial dado por F(x,y)=M(x,y)i+N(x,y)j é conservativo sse
∂N ∂M
=
.
∂x
∂y
Antes de ver uma condição necessária e suficiente para ver se um campo vectorial é
conservativo no espaço, vamos ver algumas definições:
Definição: Gradiente, é um operador que, em três dimensões, é dado por
∇=i
∂
∂
∂
+ j +k .
∂x
∂y
∂z
Nota: Conhecemos já o gradiente, mas ligado a uma função.
Definição: O rotacional de F(x,y,z)=M(x,y,z)i+N(x,y,z)j+P(x,y,z)k, onde M, N e P têm
derivadas parciais em alguma região é dado por
i
j
k
∂
rot F = ∇ x F=
∂x
∂
∂y
∂
,
∂z
M
N
P
isto é,
⎛ ∂ P ∂ N ⎞ ⎛ ∂M ∂ P ⎞
⎛ ∂ N ∂M ⎞
⎟⎟i + ⎜
⎟k .
−
−
−
rotF = ⎜⎜
⎟ j + ⎜⎜
∂x ⎠ ⎝ ∂x ∂y ⎟⎠
⎝ ∂ y ∂z ⎠ ⎝ ∂ z
Teorema: Se M, N e P tiverem derivadas parciais de primeira ordem contínuas numa bola
aberta Q, o campo vectorial dado por F(x,y,z)=M(x,y,z)i+N(x,y,z)j+P(x,y,z)k é
conservativo sse rotF=0, isto é sse
∂P ∂N ∂P ∂M ∂N ∂M
,
,
.
=
=
=
∂y ∂z
∂x ∂z
∂x
∂y
1.2. Integrais curvilíneos
O conceito de integral curvilíneo é uma generalização do integral definido.
⎧x = g( t )
, a ≤ t ≤ b , com g e h funções
Seja C uma curva dada parametricamente por ⎨
⎩ y = h( t )
definidas em [a,b]. Seja f uma função definida numa região R que contém C. Sejam A e B
os pontos de C determinados por t=a e t=b. Consideremos para sentido positivo, ao longo
de C, o sentido dos valores crescentes de t.
1. Elementos de Análise Vectorial
5
Consideremos uma partição do intervalo [a,b] da forma a=t0<t1<….<tn=b.
Esta partição conduz à partição de C em n sub-arcos Pi −1 Pi , onde Pi=(xi,yi) é o ponto
correspondente a ti. Sejam ∆si o comprimento do arco Pi−1Pi , ∆xi=xi-xi-1 e ∆yi= yi-yi-1. A
norma da partição de C, ∆ é o maior dos comprimentos ∆si.
Se, para cada um dos arcos, escolhermos um ponto Qi (ui,vi) e multiplicarmos a sua
imagem por f, pelo comprimento do arco, obtemos a soma
n
∑ f (ui , vi )∆si .
i =1
Pi
yi
vi
yi-1
Q1 P1
A=P0
x0
x1
P2
x2
Pi-1
Qi
Pn=B
C
xi-1 ui xi
xn
Se, como nos integrais definidos, existe limite, L, desta soma, quando n→∞ e
∆ →0,
independente da partição de [a,b] e dos pontos considerados em cada um dos arcos, então
L é chamado integral curvilíneo de f ao longo de C e escreve-se
∫ f ( x, y )ds .
c
Se a função f for contínua em R então o limite de
n
∑ f (ui , vi )∆si existe e é o mesmo para
i =1
todas as representações paramétricas de C com a mesma orientação.
Tudo o que foi visto pode ser generalizado para o caso da curva ser do espaço.
Definição: Seja f uma função definida numa região que contém uma curva C. O integral
curvilíneo de f ao longo de C, de A para B é dado por
∫
c
no plano e por
f ( x, y )ds = lim
n
∑ f (ui , vi )∆si
∆ → 0 i =1
1. Elementos de Análise Vectorial
6
∫ f ( x , y , z )ds =
c
n
lim
∑ f ( u i , v i , w i ) ∆ si
∆ → 0 i=1
no espaço, caso exista o limite.
Note-se que:
∆si
Pi
∆yi
Pi-1
∆xi
Então
⎛ ∆x
∆ si ≈ ∆ xi + ∆ y i = ⎜⎜ i
⎝ ∆t i
2
2
2
2
⎞
⎛ ∆y ⎞
⎟⎟ + ⎜⎜ i ⎟⎟ ∆t i
⎠
⎝ ∆t i ⎠
n
⎛ ∆x
Logo ∫ f ( x, y )ds = lim ∑ f (u i , vi ) ⎜⎜ i
∆ → 0 i =1
⎝ ∆t i
c
2
⎞
⎛ ∆y
⎟⎟ + ⎜⎜ i
⎠
⎝ ∆t i
Isto sugere-nos uma maneira mais fácil de calcular
2
⎞
⎟⎟ ∆t i
⎠
∫ f ( x, y )ds
c
Teorema: Seja f contínua numa região que contém uma curva suave C. Se C for dada
⎧x = g( t )
, a ≤ t ≤ b , então
por ⎨
⎩ y = h( t )
∫
c
b
f ( x, y )ds = ∫ f ( g (t ), h(t )) [g ' (t )]2 + [h' (t )]2 dt
a
⎧ x = g( t )
⎪
Se C for dada por ⎨ y = h( t ), a ≤ t ≤ b , então
⎪z = m( t )
⎩
b
2
2
2
∫ f ( x, y, z )ds = ∫ f ( g( t ), h( t ), m( t )) [ g '( t )] + [ h'( t )] + [ m'( t )] dt .
c
a
Se uma curva C for a reunião de um número finito de curvas, em que o último ponto de
uma, coincide com o primeiro da seguinte, o integral curvilíneo de f ao longo da curva C, é
igual à soma dos integrais curvilíneos ao longo de cada uma das curvas individuais.
1. Elementos de Análise Vectorial
7
Exemplo: Calcule ∫ xy 2 ds para C dada por x=cost, y=sent, 0≤ t ≤
c
π
2
.
π
2
2
2
2
2
∫ xy ds = ∫ cos t.sen t ( −sent ) + cos t dt =
0
c
π
⎡ sen3t ⎤ 2 1
=⎢
⎥ =
3
⎣⎢ 3 ⎦⎥ 0
As propriedades do integral curvilíneo podem ser demonstradas da mesma forma que para
os outros integrais.
Geometricamente, se f(x,y)≥0 em R, f (u i , vi )∆si dá a área de uma faixa com base Pi−1Pi
do plano xy e altura f (u i , vi ) . O limite da soma dá a área da parte de um “cilindro” de
directriz C e geratrizes paralelas ao eixo dos zz, situada entre a superfície z=f(x,y) e o
plano xy.
Podemos obter dois tipos diferentes de integrais curvilíneos utilizando ∆xi e ∆yi em lugar
de ∆si . São chamados integrais curvilíneos de f ao longo de C em relação a x e a y,
respectivamente.
Assim
∫
f ( x, y )dx = lim
∫
f ( x, y )dy = lim
∑ f (ui , vi )∆xi
∆ →0 i =1
c
n
∑ f (ui , vi )∆yi
∆ →0 i =1
c
Podemos também escrever
n
B
∫ f ( x, y )dx
A
e
B
∫ f ( x, y )dy , para evidenciar os extremos de C.
A
Teorema: Seja f contínua numa região que contém uma curva suave C. Se C for dada
⎧x = g( t )
por ⎨
, a ≤ t ≤ b , então
⎩ y = h( t )
∫
c
e
b
f ( x, y )dx = ∫ f ( g (t ), h(t )).g ′(t )dt
a
1. Elementos de Análise Vectorial
∫
c
8
b
f ( x, y )dy = ∫ f ( g (t ), h(t )).h ′(t )dt
a
Exemplo 1:
∫ f ( x, y )dx
Calcule
e
c
∫ f ( x, y )dy ,
sendo f(x,y)=xy2 e C a parte da parábola y=x2 de
c
A=(0,0) a B=(2,4)
⎧⎪ x = t
, 0 ≤ t ≤ 2 . Então
⎪⎩ y = t 2
A curva pode ser parametrizada por ⎨
2
∫
f ( x, y )dx = ∫ xy dx = ∫ t.t 4 .1dt =
∫
f ( x, y )dy = ∫ xy 2 dy = ∫ t.t 4 .2tdt =
c
c
2
0
c
2
c
0
2 6 32
=
6
3
28
7
Exemplo 2:
Calcule
∫ yzdx + xzdy + xydz , onde C é dada por x=t,y=t ,z=t ; 0≤t≤2.
2
3
c
∫ yzdx + xzdy + xydz =
c
∫ (t t
2
0
2 3
)
2
+ t.t 3 .2t + t.t 2 .3t 2 dt = ∫ 6t 5 dt = 64
0
Teorema: Sendo C uma curva percorrida no sentido de A para B, designemos por -C a
curva percorrida em sentido contrário, isto é de B para A. Temos:
(i)
∫ f ( x, y )ds = ∫ f ( x, y )ds
c
(ii)
∫ f ( x, y )dx = − ∫
f ( x , y )dx
∫ f ( x, y )dy = − ∫
f ( x , y )dy
c
(iii)
−c
c
−c
−c
Os integrais curvilíneos servem para calcular algumas quantidades, tais como áreas,
comprimento de arcos, trabalho.
1. Elementos de Análise Vectorial
9
Exemplo: Determine a área da superfície de geratrizes
paralelas ao eixo dos zz e de directriz a circunferência
x 2 + y 2 = 1 , situada entre o plano xy e o parabolóide
z = 1− x2 .
A área pode ser calculada através do integral curvilíneo
∫ (1 − x
2
)ds , sendo C a circunferência.
c
Então,
atendendo
a
que
uma
parametrização
da
circunferência
pode
ser
⎧ x = cos t
,0 ≤ t ≤ 2π
⎨
⎩ y = sin t
2
A = ∫ (1 − x )ds =
c
2π
∫ (1 − cos
2
2
2π
2
t ) (− sin t ) + cos t dt =
0
∫ sin
2
tdt = π
0
Teorema: Sendo C uma curva suave quer no plano quer no espaço, o comprimento do
arco L, é dado por
L=
∫c ds
O calculo do trabalho realizado por uma força quando um objecto se desloca sobre uma
curva C é uma das suas aplicações físicas mais importantes.
Começamos por subdividir C como anteriormente em arcos Pi −1 Pi e seja Qi(ui,vi,wi)∈
Pi −1 Pi .
Se
∆
é
pequena,
então
o
trabalho
realizado
por
F(x,y,z)=
M(x,y,z)i+N(x,y,z)j+P(x,y,z)k ao longo do arco Pi −1 Pi , ∆Wi, pode ser aproximado pelo
trabalho realizado pela força constante F(ui,vi,wi), quando o seu ponto de aplicação se
desloca ao longo do vector Pi −1 Pi . O vector Pi −1 Pi corresponde ao vector (∆xi,∆yi,,∆zi) de
V3.
→
Como o trabalho realizado por uma força constante PQ , quando o seu ponto de aplicação
→
→
→
se desloca ao longo de um vector PR é dado por PQ . PR , no nosso caso temos que
∆Wi≈ F(ui,vi,wi). (∆xi,∆yi,,∆zi)= M(ui,vi,wi)∆xi+N(ui,vi,wi)∆yi +P(ui,vi,wi)∆zi
Podemos então estabelecer:
1. Elementos de Análise Vectorial
10
Definição: Se C é uma curva suave num campo de forças F, o trabalho realizado por F ao
∑ ∆Wi ,
longo de C é dado por W=
∆ →0
isto é
W =
∑ M(ui ,vi ,wi )∆xi + N(ui ,vi ,wi )∆yi + P(ui ,vi ,wi )∆zi ,
∆ →0
donde
W= ∫ M(x,y,z)dx+N(x,y,z)dy+P(x,y,z)dz
C
Nota: O trabalho determina-se de forma análoga para um campo vectorial no plano.
Por outro lado, como o arco é muito pequeno, podemos assumir que a partícula se move aí,
na direcção do vector tangente unitário Ti(ui, vi, wi). Sendo assim
∆Wi≈ F(ui,vi,wi). (∆si. Ti(ui, vi, wi))=( F(ui,vi,wi). Ti(ui, vi, wi)) ∆si
Podemos então escrever:
Definição: Sendo C é uma curva suave num campo de forças F e T(x,y,z) o vector tangente
unitário a C no ponto P(x,y,z), o trabalho W realizado por F ao longo de C é dado por
∫ F ( x, y, z ).T ( x, y, z )ds
c
Nota: As duas fórmulas são equivalentes, atendendo a que
T =
dr
,
ds
sendo
r (t ) = x(t )i + y (t ) j + z (t )k .
b
W= ∫ F .Tds = ∫ F .
c
a
dr dt
ds = ∫ F .dr = ∫ Mdx + Ndy + Pdz , sendo F = Mi + Nj + Pk .
dt ds
c
c
Exemplo:
Determinar o trabalho realizado pelo campo de forças F ( x, y, z ) = xi − xyj + z 2 k , para
mover uma partícula ao longo da hélice dada por r(t) = cos ti + sentj + tk , desde o ponto
(0,0,0) até (-1,0,3π).
1. Elementos de Análise Vectorial
11
W = ∫ Mdx + Ndy + Pdz = ∫ xdx − xydy + z 2 dz =
c
3π
c
3π
3π
∫ (cos t (−sent ) − cos t.sent. cos t + t
2
)dt =
0
3π
⎡t 3 ⎤
⎡ cos 3 t ⎤
⎡ cos 2 t ⎤
2
3
+
+
=⎢
⎢ ⎥ = − + 9π
⎥
⎢
⎥
3
⎢⎣ 3 ⎥⎦ 0
⎢⎣ 3 ⎥⎦ 0
⎢⎣ 2 ⎥⎦ 0
Nota: O trabalho realizado por um campo de forças pode ser negativo. Isto acontece
quando o campo impede o movimento ao longo da curva. Na figura seguinte vemos um
caso em que isso acontece.
1.3. Independência do caminho
Se determinarmos o integral curvilíneo, ∫ F .dr , num campo vectorial conservativo, ao
c
longo de três caminhos distintos, vemos que o valor não se altera.
Podemos constatar isso com a resolução do problema seguinte:
Calcular o trabalho realizado pelo campo de forças F(x,y)=4xyi + 2x2j quando uma
partícula se move de (0,0) a (1,1) ao longo dos caminhos i) y=x; ii) x=y2; iii) y=x3.
Isto é-nos garantido pelo teorema:
Teorema fundamental dos integrais curvilíneos: Seja C uma curva suave, contida numa
⎧x = g( t )
região aberta R, dada por ⎨
, a ≤ t ≤ b . Se F(x,y)=M(x,y)i+N(x,y)j é conservativo
⎩ y = h( t )
em R e M e N são contínuas em R, então
1. Elementos de Análise Vectorial
12
∫ F .dr = ∫ ∇f .dr = f ( g (b), h(b)) − f ( g (a), h(a))
c
c
em que f é uma função potencial de F.
Nota: Este teorema é aplicável para curvas contidas numa região do espaço.
Temos então que se o campo vectorial é conservativo o integral curvilíneo de F.dr entre
dois quaisquer pontos, é igual à diferença da função potencial nesses pontos. Sendo assim
num campo conservativo o valor do integral curvilíneo ∫ F.dr é o mesmo para qualquer
c
curva suave C contida em R entre dois pontos fixos. Dizemos então que
∫ F.dr é
c
independente do caminho na região R.
Teorema: Se F é contínua numa região aberta e convexa, então o integral curvilíneo
∫ F.dr é independente do caminho se e só se F=∇f para algum f, isto é, se e só se o campo
c
F é conservativo.
Exemplo: Seja F(x,y)=(2x+y3)i+(3xy2+4)j. Mostre que o integral curvilíneo ∫ F.dr é
c
(2,3)
independente do caminho e calcule ∫ F.dr .
(0,1)
O integral é independente do caminho sse
Como,
∂N ∂M
=
.
∂x
∂y
∂M
∂N
= 3y 2 e
= 3 y 2 , é independente do caminho.
∂y
∂x
(2,3)
Sendo assim
∫ F.dr =
f (2,3) − f (0,1)
(0,1)
C.A.
∂f
∂f
= 3 y 2 x + k ′( y )
= 2 x + y 3 ⇒ f ( x, y ) = x 2 + y 3 x + k ( y ) ⇒
∂y
∂x
∂f
= 3 xy 2 + 4
∂y
k ′( y ) = 4 ⇒ k ( y ) = 4 y + C
Logo f ( x, y ) = x 2 + y 3 x + 4 y + C
1. Elementos de Análise Vectorial
( 2 ,3 )
Então
∫ F.dr = f (2,3) − f (0,1) = 2
13
2
+ 33.2 + 4.3 + C − 4 − C = 66
( 0 ,1 )
1.4. Teorema de Green
O teorema de Green diz-nos que o integral duplo sobre uma região simplesmente convexa1
R é igual ao valor do integral curvilíneo sobre a fronteira de R.
Teorema de Green: Seja R uma região simplesmente convexa e C a sua fronteira,
considerada com sentido positivo (contrário ao dos ponteiros do relógio). Se M e N são
funções contínuas com derivadas parciais de 1ª ordem também contínuas numa região
aberta D que contém R, então
⎛ ∂N
∫ Mdx + Ndy = ∫∫ ⎜⎜⎝ ∂x −
C
R
∂M
∂y
⎞
⎟⎟dA
⎠
Demonstração: Para mostrar esta igualdade temos de provar que
∫ Mdx = −∫∫
C
que ∫ Ndy = ∫∫
C
R
R
∂M
dA e
∂y
∂N
dA . Vamos mostrar apenas a segunda igualdade, pois de modo análogo
∂x
se prova a outra. Consideremos uma região R
d
C
x=g1(y)
R
x=g2(y)
c
Temos
d
c
c
d
∫ N ( x, y)dy = ∫ N ( x, y)dy + ∫ N ( x, y)dy = ∫ N ( g 2 ( y), y)dy + ∫ N ( g1 ( y), y)dy =
C
C1
C2
d
d
c
c
∫ N ( g 2 ( y), y)dy − ∫ N ( g1 ( y), y)dy
Por outro lado
1
Uma curva plana diz-se simples se não se cruza em si mesma. Uma região plana R é simplesmente convexa se é
limitada por uma única curva fechada simples.
1. Elementos de Análise Vectorial
d g2 ( y)
∂N
∫∫ ∂x ( x, y)dA = ∫
R
∫
c g1 ( y )
14
d
∂N
g ( y)
( x, y )dxdy = ∫ [N ( x, y )]g 2( y ) dy
1
∂x
c
d
=
∫ [N ( g 2 ( y), y) − N ( g1 ( y), y)]dx
c
Exemplos:
1. Calcule ∫ 5 xydx + x 3dy , onde C é a curva dada por y=x2 e y=2x de (0,0) a (2,4)
C
∫ 5xydx + x
C
2 2x
∫ ∫ (3x
2
∫ (− 3x
4
0 x2
2
3
(
)
dy = ∫∫ 3x 2 − 5 x dA =
R
)
2
[
]
2x
− 5 x dydx = ∫ 3 x 2 y − 5 xy x 2 dx =
0
)
+ 11x 3 − 10 x 2 dx =
0
2
⎡ x5
28
x4
x3 ⎤
= ⎢− 3
+ 11
− 10 ⎥ = −
5
4
3 ⎦⎥
15
⎣⎢
0
2. Calcule
3x
∫ x 2 + y 2 dx + 2 xdy , sendo C o quadrado [-1,2]x[-1,2]
c
Como a função M ( x, y ) =
3x
x2 + y2
não é contínua em (0,0), não
2
C3
podemos utilizar o teorema de Green. Sendo assim vamos calcular o
C4
integral curvilíneo por definição, calculando o integral ao longo de
cada um dos 4 caminhos, C1, C2, C3 e C4.
Comecemos por parametrizar os caminhos:
⎧x = t
⎧x = 2
, −1 ≤ t ≤ 2 , C 2 : ⎨
C1 : ⎨
, −1 ≤ t ≤ 2 ,
⎩ y = −1
⎩y = t
⎧x = t
⎧ x = −1
− C3 : ⎨
, −1 ≤ t ≤ 2
, −1 ≤ t ≤ 2 , − C 4 : ⎨
⎩y = 2
⎩y = t
Então
C1
-1
-1
C2
2
1. Elementos de Análise Vectorial
3x
15
3x
3x
∫ x 2 + y 2 dx + 2 xdy = ∫ x 2 + y 2 dx + 2 xdy + ∫
c
−
2
2
2
C2 x + y
C1
3x
∫
2
C3 x + y
2
dx + 2 xdy −
2
3t
∫
3x
2
C4 x + y
2
2
dx + 2 xdy −
dx + 2 xdy =
2
3t
∫ t 2 + 1dt + ∫ 4dt − ∫ t 2 + 4dt + ∫ 2dt =
−1
−1
−1
−1
2
2
3 8
3 25
3 5
⎡3
⎤
⎡3
⎤
2
2
2
⎢⎣ 2 ln t + 1 ⎥⎦ + [6t ]−1 − ⎢⎣ 2 ln t + 4 ⎥⎦ = 2 ln( 2 ) + 18 − 2 ln( 5 ) = 2 ln( 16 ) + 18
−1
−1
O teorema de Green também pode ser utilizado para obter uma fórmula para calcular a
área de uma região limitada por uma curva fechada simples parcialmente suave C.
Com efeito, se em
⎛ ∂N
∫ Mdx + Ndy = ∫∫ ⎜⎜⎝ ∂x
C
∫∫ 1dA = ∫ xdy
R
R
−
∂M
∂y
e se fizermos M=y e N=0 temos
C
⎞
⎟⎟dA fizermos M=0 e N=x, temos
⎠
∫∫1dA = − ∫ ydx . Como ∫∫1dA
R
C
nos dá a
R
área de R, destas duas igualdades podemos tirar que
A=
1
xdy − ydx .
2∫
C
Exemplo: Calcule a área da região limitada pela elipse
1
1
A = ∫ xdy − ydx =
2
2
C
2π
=
x2
a2
+
2π
2π
0
0
1
∫ (a cos t.b cos t + bsent.asent )dt = 2
y2
b2
=1
∫ (ab cos
2
)
t + absen 2 t dt =
ab
ab 2π
[t ] = πab
1dt =
∫
2
2 0
0
1.5. Integrais de Superfície
Vamos agora considerar um integral de uma função sobre uma superfície. Seja S o gráfico
de z=f(x,y), em que a sua projecção R num dos planos coordenados, neste caso considerase xy, é uma região do tipo das que aparecem nos integrais duplos. Suponhamos que f tem
derivadas parciais de primeira ordem contínuas. O integral de uma função g(x,y,z) sobre
uma superfície S, sendo g definida numa região que contém S obtém-se de modo análogo
ao que tem sido feito até aqui. Considera-se uma partição interior de R em rectângulos Ri .
Considera-se um ponto Pi(xi, yi, 0) em cada um desses rectângulos. A este ponto
1. Elementos de Análise Vectorial
16
corresponde o ponto Bi(xi, yi, zi) de S. Considera-se também o plano tangente a S em Bi .
Seja ∆Si a área da superfície de S e ∆Ti a área da região do plano tangente cuja projecção
em R é o rectângulo Ri . Quando a norma da partição tende para zero, a área ∆Ti é uma
boa aproximação para a área ∆Si e sendo assim Σ∆Ti é uma boa aproximação para a área
n
de S. Podemos considerar a soma ∑ g ( xi , y i , z i )∆Ti . Se existir o limite desta soma quando
i =1
a norma da partição tender para zero, esse limite dá o integral de superfície de g sobre S e
escreve-se
∫∫ g( x , y , z )dS .
S
Definição: Seja g uma função definida numa região que contém uma superfície S. O
integral de superfície de g sobre S é dado por
∫∫ g( x , y , z )dS =
S
n
lim
∑ g( xi , yi , zi )∆Ti
∆ →0 i = 1
desde que o limite exista.
Teorema: Seja S uma superfície de equação z=f(x,y) e R a sua projecção no plano xy. Se f
é contínua em R e tem aí derivadas de 1ª ordem contínuas e g é contínua em S, então o
integral de superfície de g sobre S é dado por
2
2
∫∫ g ( x, y, z )dS = ∫∫ g ( x, y, f ( x, y)) [ f x ( x, y)] + [ f y ( x, y)] + 1dA
S
R
Nota: Se g(x,y,z)=1 então o integral de superfície dá a área da superfície S.
Exemplo: Calcule ∫∫ x 2 zdS , onde S é a porção do cone z2=x2+y2 que está entre os planos
S
z=1 e z=4.
∫∫ x
S
2
zdS = ∫∫ x
2
x +y
2
R
2
x2
y2
+
+ 1dA =
x2 + y2 x2 + y2
2π 4
(
)
= 2 ∫∫ x 2 x 2 + y 2 dA = 2 ∫ ∫ ρ 2 cos 2 θρρ dρdθ =
0 1
R
4
2π
⎡ρ5 ⎤
⎛ 4 5 1 ⎞2π 1 + cos 2θ
= 2 ∫ cos θ ⎢ ⎥ dθ = 2 ⎜⎜ − ⎟⎟ ∫
dθ =
2
⎣ 5 ⎦1
⎝ 5 5⎠ 0
0
2
z = x2 + y2
2x
fx =
2 x2 + y2
2y
fy =
2 x2 + y2
1. Elementos de Análise Vectorial
17
2π
⎛ 45 1 ⎞ ⎡ 1
⎛ 45 1 ⎞
1
⎤
= 2 ⎜⎜ − ⎟⎟ ⎢ θ + sen2θ ⎥ = 2 ⎜⎜ − ⎟⎟π
4
⎦0
⎝ 5 5 ⎠⎣ 2
⎝ 5 5⎠
Se a equação de S é y=h(x,z), onde h tem derivadas parciais de primeira ordem contínuas e
S tem projecção R1 regular sobre o plano xz então
2
2
∫∫ g ( x, y, z )dS = ∫∫ g ( x, h( x, z ), z ) [h x ( x, z )] + [h z ( x, z )] + 1dA
S
R1
De modo análogo, se a equação de S é x=m(y,z), onde m tem derivadas parciais de
primeira ordem contínuas e S tem projecção R2 regular sobre o plano yz então
2
2
∫∫ g ( x, y, z )dS = ∫∫ g (m( y, z ), y, z ) [m y ( y, z )] + [m z ( y, z )] + 1dA
S
R2
No cálculo de alguns integrais curvilíneos utilizámos vectores tangentes à curva C.
Podemos proceder de modo análogo, considerando agora vectores normais à superfície S.
Pode não existir vector normal a uma superfície, mas no caso de existir pode calcular-se
através do vector gradiente.
Seja uma superfície S dada por z=f(x,y). Um vector normal a esta superfície é o vector
gradiente da função g(x,y,z)=z-f(x,y), isto é
∇g ( x , y , z ) = g x ( x , y , z )i + g y ( x , y , z ) j + g z ( x , y , z )k = − f x ( x , y )i − f y ( x , y ) j + k
Um vector normal unitário à superfície, n, será o versor de ∇g ( x, y, z ) , isto é
n=
Nota: O vector − n = −
∇g ( x , y , z )
=
∇g ( x , y , z )
− f x ( x , y )i − f y ( x , y ) j + k
( f x ( x , y ))2 + ( f y ( x , y ))2 + 1
∇g ( x , y , z )
é também um vector unitário, normal à superfície. É
∇g ( x , y , z )
um vector normal unitário inferior.
Se a superfície for dada por y=h(x,z), um vector normal a esta superfície é o vector
gradiente da função g(x,y,z)=y-h(x,z), isto é
∇g ( x , y , z ) = g x ( x , y , z )i + g y ( x , y , z ) j + g z ( x , y , z )k = −h x ( x , z )i + j − h z ( x , z )k
e de modo análogo se calcula um vector normal à superfície dada por x=m(y,z).
1. Elementos de Análise Vectorial
18
Nota: Se for possível calcular um vector normal a cada ponto de uma superfície S, então
essa superfície é chamada orientada.
Se a superfície S for fechada a orientação positiva é aquela em que os vectores normais são
exteriores à superfície e a orientação negativa é aquela em que os vectores são interiores à
superfície.
Definição: Se existir um vector normal unitário, n, a qualquer ponto da fronteira de S,
∫∫ F .ndS
define vectorialmente um integral de superfície, sendo F um campo vectorial
S
definido numa região que contém S.
Uma das aplicações dos integrais de superfície é o cálculo do volume de um fluido que
atravessa uma superfície S.
Suponhamos uma superfície S, com vector normal unitário n, a qualquer ponto, submersa
num fluido que tem um campo de velocidades contínuo v e uma densidade ρ. Seja ∆Si a
área de uma pequena região de S. Sendo essa região muito pequena podemos aí considerar
a força constante. Então a quantidade de fluido que atravessa ∆Si na unidade de tempo,
taxa de vazão, pode ser aproximada pelo volume de um cilindro de área de base ∆Si e
altura F.n (F=(ρv)).
(2)
F.n
(1)
F.T
(1)
é a componente tangencial da velocidade (força) (ao longo da superfície). Esta não
influi no fluxo através de S.
(2)
Componente normal da velocidade (perpendicular à superfície).
Então
∆Vi=(F.n) ∆Si
1. Elementos de Análise Vectorial
19
Somando todas as quantidades e calculando o limite, obtemos
∫∫ F .ndS , que fisicamente
S
nos dá a taxa de vazão através de S.
Definição: Seja F(x,y,z)=M(x,y,z)i+N(x,y,z)j+P(x,y,z)k, onde M, N e P têm derivadas
parciais de 1ª ordem contínuas na superfície S, tendo esta superfície n como vector normal
unitário. O fluxo de F através de S por unidade de tempo é dado por
∫∫ F .ndS
S
Exemplo: Seja S a parte do parabolóide z = 4 − x 2 − y 2 situada acima do plano xy . Essa
superfície tem um vector normal unitário superior. Um fluido de densidade 1 com um
campo de velocidades v(x,y,z)=xi+yj+zk, flue através da superfície S. Determine o fluxo
de F através de S.
F = ∫∫ F .ndS = ∫∫
S
=
∫∫
S
∫∫ x
Rxoy
2
2
4x + 4 y + 1
2x 2 + 2 y 2 + 4 − x 2 − y 2
4x 2 + 4 y 2 + 1
R xoy
=
2x 2 + 2 y 2 + z
2
2
2 2π
+ y + 4dA = ∫
∫ (ρ
0 0
2
dS =
n=
4 x 2 + 4 y 2 + 1dA =
)
2
=
(
∇
=
∇
2 xi + 2 yi + 1k
4x 2 + 4 y 2 + 1
)
+ 4 ρ dθdρ = 2π ∫ ρ 3 + 4 ρ dρ = 24π
0
Nota: Os integrais de fluxo podem escrever-se de uma forma mais simplificada atendendo
⎛ ∇g ( x , y , z )
a que ⎜⎜
⎝ ∇g ( x , y , z )
⎞
⎟dS = ∇g ( x, y, z )dA
⎟
⎠
Teorema: Se S é uma superfície dada por z=g(x,y) e R é a sua projecção no plano xy,
então
∫∫ F .ndS = ∫∫ F .(− g x ( x, y)i − g y ( x, y) j + k )dA
S
R
ou
∫∫ F .ndS = ∫∫ F .( g x ( x, y)i + g y ( x, y) j − k )dA
S
R
conforme o vector normal unitário é superior ou inferior.
1. Elementos de Análise Vectorial
20
1.6. Teoremas de Gauss e de Stokes
Vamos começar por definir uma função num campo vectorial.
Definição: A divergência de F(x,y)=Mi+Nj é
divF ( x, y ) = ∇.F ( x, y ) =
∂M ∂N
+
∂x ∂y
A divergência de F(x,y,z)=Mi+Nj+Pk é
divF ( x, y, z ) = ∇.F ( x, y, z ) =
∂M ∂N ∂P
+
+
∂x ∂y ∂z
O teorema de Green diz-nos que, sendo F(x,y)=M(x,y)i+N(x,y)j e C uma curva fechada
que delimita uma região R, nas condições do teorema
⎛ ∂N
∫ F .Tds = ∫ Mdx + Ndy = ∫∫ ⎜⎜⎝ ∂x
C
C
−
R
∂M
∂y
⎞
⎟⎟dA
⎠
Se T=x'(t)i+y'(t)j for um vector unitário tangente à curva, um vector normal unitário para
fora da região R será n=y'(t)i-x'(t)j.
Para a mesma função F, podemos, utilizando o teorema de Green, calcular ∫ F .nds .
C
⎛ ∂N
∫ F .nds = ∫ Mdy − N dx = ∫∫ ⎜⎜⎝ ∂y
C
C
+
R
∂M
∂x
⎞
⎟⎟dA = ∫∫ divF dA .
⎠
R
Podemos generalizar este resultado para superfícies fechadas.
Teorema de Gauss (ou divergência): Seja Q uma região limitada por uma superfície
fechada
S,
com
vector
unitário
normal
exterior
a
Q.
Se
F(x,y,z)=M(x,y,z)i+N(x,y,z)j+P(x,y,z)k é um campo vectorial, em que as funções M, N e P
têm derivadas parciais de primeira ordem contínuas em Q, então
∫∫ F ⋅ n dS = ∫∫∫ divF dV
S
Q
Demonstração:
A igualdade pode escrever-se da forma
⎛ ∂M
∫∫ (Mi.n + Nj.n + Pk.n )dS = ∫∫∫ ⎜⎜⎝ ∂x
S
Q
+
∂N ∂P ⎞
⎟dV
+
∂y ∂z ⎟⎠
Para provar esta igualdade temos de mostrar que
1. Elementos de Análise Vectorial
∂M
∫∫ (Mi.n)dS = ∫∫∫ ∂x
S
21
dV
Q
∂N
∫∫ (N j.n)dS = ∫∫∫ ∂y dV
S
Q
∂P
∫∫ (Pk.n )dS = ∫∫∫ ∂z dV
S
Q
Vamos mostrar apenas a última igualdade, considerando um caso particular de Q e de S.
Consideremos a região Q com superfície superior S2 de equação z=g2(x,y) e superfície
inferior S1 de equação z=g1(x,y), cujas projecções no plano xy formam a região R.
Se Q tem uma superfície lateral, o vector normal é horizontal sendo portanto Pk.n=0.
Logo
∫∫ Pk.ndS = ∫∫ Pk.ndS + ∫∫ Pk.ndS + 0 .
S
S1
S2
Como o vector normal unitário a S2 é superior e o vector normal unitário a S1 é inferior,
então por um teorema visto atrás,
⎛ ∂g1
∫∫ Pk.ndS = ∫∫ P( x, y, g1 ( x, y))k.⎜⎜⎝ ∂x
S1
i+
R
∂g1
⎞
j − k ⎟⎟dA = − ∫∫ P( x, y, g1 ( x, y ))dA
∂y
⎠
R
e
∂g
⎛ ∂g 2
⎞
i − 2 j + k ⎟⎟dA = ∫∫ P( x, y, g 2 ( x, y ))dA
∂x
∂y
⎠
∫∫ Pk.ndS = ∫∫ P( x, y, g 2 ( x, y))k.⎜⎜⎝ −
S2
R
R
Somando estes dois resultados, obtemos
∫∫ Pk.ndS = ∫∫ [P( x, y, g 2 ( x, y)) − P( x, y, g1 ( x, y))]dA =
S
R
⎤
⎡ g 2 ( x, y )
∂P
∂P ⎥
⎢
∫∫ ⎢ ∫ ∂z dz ⎥dA = ∫∫∫ ∂z dV
R ⎣ g1 ( x , y )
Q
⎦
Exemplo: Seja Q a região limitada pelo gráfico de x2+y2=4, z=0 e z=3. Seja S a superfície
de Q, e n o vector unitário de uma normal exterior a S.
Se F(x,y,z)= x3 i +y3 j +z3 k, use o teorema de Gauss para calcular
∫∫ F ⋅ ndS .
S
1. Elementos de Análise Vectorial
22
(
2 2π 3
)
∫ ∫ (ρ
2
2
2
∫∫ F ⋅ ndS = ∫∫∫ divFdV = ∫∫∫ 3x + 3 y + 3z dV = 3∫
S
Q
2
)
+ z 2 ρdzdθdρ =
0 0 0
Q
3
2 2π
2
⎡ 3
z3 ⎤
3
= 3∫ ∫ ⎢ ρ z +
ρ ⎥ dθ dρ = 3∫ ∫ 3ρ + 9 ρ dθ dρ = 9∫ ρ 3 + 3ρ [θ ]02π dρ =
3 ⎥⎦
0 0 ⎣⎢
0 0
0
0
[
2 2π
]
(
)
2
⎡ρ4
ρ2 ⎤
=⎢
+3
⎥ = 18π (6 + 4) = 180π
2 ⎥⎦
⎢⎣ 4
0
O teorema de Green pode escrever-se de outro modo:
⎛ ∂N
+ Ndy = ⎜
∫ Mdx
14243 ∫∫ ⎜⎝ ∂x
C
−
R
F .Tds
∂M
∂y
⎞
⎟⎟dA = ∫∫ rotF .kdA .
⎠
R
Uma generalização deste teorema é o teorema de Stokes que relaciona um integral de
superfície sobre uma superfície S e um integral curvilíneo ao longo de uma curva fechada
C que é fronteira de S.
Teorema de Stokes: Seja S uma superfície com um vector normal unitário n, limitada por
uma curva fechada simples C. Se F é um campo vectorial, onde as funções componentes
têm derivadas parciais de 1ª ordem contínuas numa região aberta que contém S e C, então
∫ F .Tds = ∫∫ rotF .ndS
C
S
Nota: A direcção positiva sobre C é considerada relativamente ao vector normal à
superfície, n.
Exemplo:
1.
Calcule
o
trabalho
realizado
por
F ( x, y, z ) = x 2 i + 4 xy 3 j + y 2 xk no rectângulo do pano
z=y representado na figura.
3
1
1. Elementos de Análise Vectorial
23
w = ∫ F .Tds = ∫∫ (rotF .n)dS =
c
Como o sentido da curva é o positivo,
o vector normal que nos interessa será
0i − 1 j + 1k
S
= ∫∫ rotF .(0i − 1 j + 1k )dA =
i
R
(
)
13
(
)
= ∫∫ y 2 + 4 y 3 dA = ∫ ∫ y 2 + 4 y 3 dydx =
R
00
3
1
⎤
y
4
= ∫⎢
+ y ⎥ dx = ∫ 90dx = 90
3
⎢
⎣
⎦⎥ 0
0
0
1⎡ 3
∂
rot F = ∇ x F=
∂x
x2
j
∂
∂y
4 xy 3
= (2 xy )i − y 2 j + (4 y 3 )k
k
∂
=
∂z
y2x