www.ruilima.com.br | facebook/RuiLima

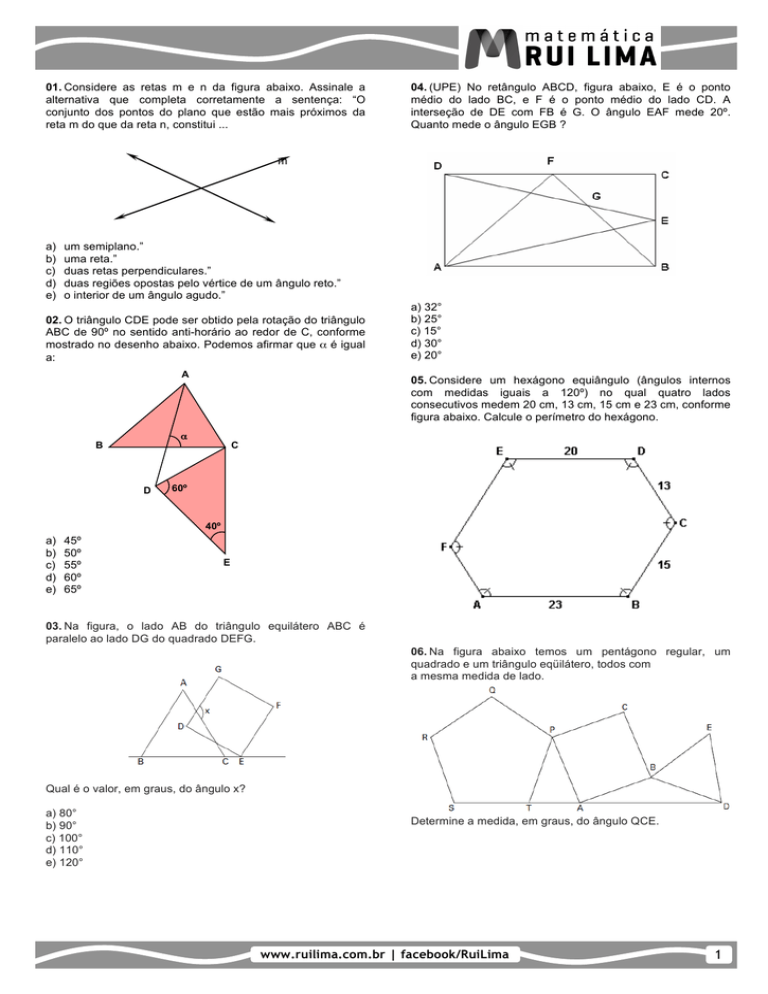
01. Considere as retas m e n da figura abaixo. Assinale a
alternativa que completa corretamente a sentença: “O
conjunto dos pontos do plano que estão mais próximos da
reta m do que da reta n, constitui ...
04. (UPE) No retângulo ABCD, figura abaixo, E é o ponto
médio do lado BC, e F é o ponto médio do lado CD. A
interseção de DE com FB é G. O ângulo EAF mede 20º.
Quanto mede o ângulo EGB ?
m
a)
b)
c)
d)
e)
um semiplano.”
uma reta.”
duas retas perpendiculares.”
duas regiões opostas pelo vértice de um ângulo reto.”
o interior de um ângulo agudo.”
02. O triângulo CDE pode ser obtido pela rotação do triângulo
ABC de 90º no sentido anti-horário ao redor de C, conforme
mostrado no desenho abaixo. Podemos afirmar que α é igual
a:
A
05. Considere um hexágono equiângulo (ângulos internos
com medidas iguais a 120º) no qual quatro lados
consecutivos medem 20 cm, 13 cm, 15 cm e 23 cm, conforme
figura abaixo. Calcule o perímetro do hexágono.
α
B
D
a) 32°
b) 25°
c) 15°
d) 30°
e) 20°
C
60º
40º
a)
b)
c)
d)
e)
45º
50º
55º
60º
65º
E
03. Na figura, o lado AB do triângulo equilátero ABC é
paralelo ao lado DG do quadrado DEFG.
06. Na figura abaixo temos um pentágono regular, um
quadrado e um triângulo eqüilátero, todos com
a mesma medida de lado.
Qual é o valor, em graus, do ângulo x?
a) 80°
b) 90°
c) 100°
d) 110°
e) 120°
Determine a medida, em graus, do ângulo QCE.
www.ruilima.com.br | facebook/RuiLima
1
07. Na figura, sabemos que AB = AC e AD = BC. Assinale a
medida do ângulo α
10. Na figura abaixo, ABC é um triângulo isósceles de base
BC. Determine α.
A
A
40º
100º
C
B
α
D
15º
35º
B
C
11. Na figura o triângulo ABC é isósceles, BÂC = 20º e BC =
BD = BE.
08. Observe esta figura:
Nessa figura, os segmentos AB e BC são perpendiculares,
respectivamente, às retas r e s. Além disso, AP = PB, BQ =
QC e a medida do ângulo PÔQ é θ. Sendo x⋅θ a medida do
ângulo interno AÔC do quadrilátero AOCB assinale o valor de
x.
Determine a medida do ângulo BDˆ E.
12. Um ponto A qualquer é considerado sobre o lado Ox do
ângulo xÔy da figura. Traçamos então:
1) AB ⊥ Ou
2) AQ // Ou
09. DEFG é um quadrado no exterior do pentágono regular
ABCDE. Quanto mede o ângulo EÂF?
3) OPQ tal que PQ = 2 OA.
X
A
Q
P
a) 9° d) 18°
b) 12° e) 21°
c) 15°
O
B
Y
Se PÔB = 26°, xÔy mede:
a)
b)
c)
d)
e)
61°
66°
72°
78°
o
80
www.ruilima.com.br | facebook/RuiLima
2
13. Num trapézio retângulo circunscritível, a soma dos dois
lados paralelos é igual a 18cm e a diferença dos dois outros
lados é igual a 2cm. Se r é o raio da circunferência inscrita e
a é o comprimento do menor lado do trapézio, então a soma
a+r (em cm) é igual a:
a)
b)
c)
d)
e)
12
11
10
9
8
16. Um fabricante de embalagens dispõe em seu estoque de
uma grande quantidade de peças em forma de retângulos,
quadrados, círculos e triângulos equiláteros, como as
indicadas na figura.
20 cm
14. Da figura abaixo sabe-se que:
r//s
AM ≅ AP
BM ≅ BQ
s
r
P
70 cm
As peças têm em comum a dimensão 20 cm, e as linhas
tracejadas, que dividem as figuras
em partes iguais,
representam possibilidades de cortes para a confecção das
embalagens. Com essas peças, o fabricante pretende obter
figuras prismáticas ou cilíndricas usando um retângulo na
área lateral e, nas bases, as demais figuras, inteiras ou
seccionadas por um corte. As emendas e os encaixes serão
feitos com material à parte e não precisam ser considerados.
O preço das embalagens será definido pelo peso do material,
por isso, o critério usado para decidir qual a forma da
embalagem a ser confeccionada é o de usar o material
disponível com o menor desperdício possível. Assim, a forma
escolhida para as bases da caixa deverá ser:
Q
α
A
M
a) o triângulo equilátero.
b) o triângulo retângulo isósceles.
c) o triângulo retângulo escaleno.
d) o círculo.
e) o semicírculo.
B
Então, α vale:
15. No triângulo ADE da figura, em que B e C são pontos
dos lados AD e AE, respectivamente, AB=AC, BC=BD e
CD=CE.
Então,
a) x = 48º.
b) x = 50º.
c) x = 52º.
d) x = 54º.
e) x = 56º.
Usar as seguintes
aproximações:
π = 3,14
√2 = 1,41
√3 = 1,73
17. No triângulo ABC (figura abaixo), os lados AB, AC e BC
medem respectivamente 5cm, 7cm e 9cm. Se P é o ponto de
encontro das bissetrizes dos ângulos B e C e PQ//MB,
PR//NC e MN//BC, a razão entre os perímetros dos triângulos
AMN e PQR é:
a) 10/9
b) 9/8
c) 7/6
d) 4/3
e) 7/5
18. (UFPE) Na ilustração abaixo, todos os círculos tem
mesmo raio, o triângulo ABC é equilátero e seus lados
medem 28(1+ 3) unidades de comprimento. Determine o raio
dos círculos.
www.ruilima.com.br | facebook/RuiLima
3
19. Seja AOB um ângulo medindo 36º e C o pé da
perpendicular a OB por A. Construa a reta r perpendicular a
AC passando por A. Determine o ponto D, situado entre A e
C tal que a reta por O e D intercepta r em E com ED = 2AO.
Qual a medida de AOE?
20. (UFPE) Num paralelogramo as diagonais medem 8cm e
6cm e um dos lados mede 3cm. Qual o inteiro mais próximo
do perímetro deste paralelogramo?
GABARITOS
01.
02.
03.
04.
05.
06.
07.
08.
09.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
d
C
e
E
99
174º
10
02
a
75
60º
D
C
90
c
A
D
14
24
09
www.ruilima.com.br | facebook/RuiLima
4