Tensão de Cisalhamento Máxima Absoluta

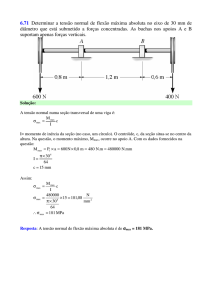
- UNIVERSIDADE FEDERAL FLUMINENSE
ESCOLA DE ENGENHARIA INDUSTRIAL METALÚRGICA DE VOLTA REDONDA
PROFESSORA: SALETE SOUZA DE OLIVEIRA BUFFONI
DISCIPLINA: RESISTÊNCIA DOS MATERIAIS
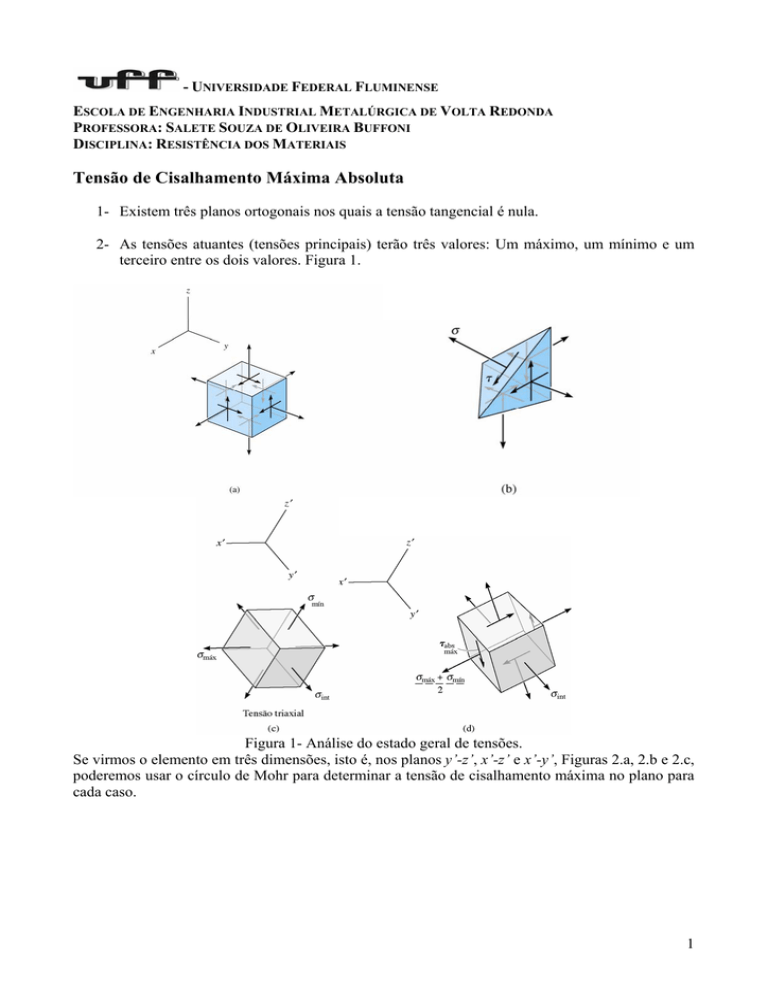
Tensão de Cisalhamento Máxima Absoluta
1- Existem três planos ortogonais nos quais a tensão tangencial é nula.
2- As tensões atuantes (tensões principais) terão três valores: Um máximo, um mínimo e um
terceiro entre os dois valores. Figura 1.
Figura 1- Análise do estado geral de tensões.
Se virmos o elemento em três dimensões, isto é, nos planos y’-z’, x’-z’ e x’-y’, Figuras 2.a, 2.b e 2.c,
poderemos usar o círculo de Mohr para determinar a tensão de cisalhamento máxima no plano para
cada caso.
1
Figura 2- Elemento em três dimensões.
3- O diâmetro do círculo de Mohr compreende as tensões principais σ int e σ min para o caso
mostrado na Figura 2.a. Pelo círculo, a tensão de cisalhamento máxima no plano é dada por:
(τ )
y' z' max
A tensão normal média é dada por:
σ med =
= (σ int − σ min ) 2
(σ int
+ σ min )
2
(1)
(2)
Como apresenta a Figura 2.e.
Figura 2 – Tensão de cisalhamento máxima para a Figura 2.a.
2
O elemento com esses componentes de tensão deve ser orientado a 45º em relação à posição do
elemento mostrado na Figura 2.a.
Os círculos de Mohr para os elementos das Figuras 2.b e 2.c também foram traçados na Figura 2.d.
Os elementos com orientação de 45º e sujeitos aos componentes das tensões de cisalhamento
máxima no plano e normal média são apresentados nas Figuras 2.f e 2.g, respectivamente.
Figura 2 – Tensão de cisalhamento máxima para a Figura 2.b e 2.c, respectivamente.
Comparando-se os três círculos da Figura 2.d vê-se que a tensão de cisalhamento máxima absoluta
será definida pelo círculo que tenha o maior raio, Figura 2.b. Dessa forma tem-se:
σ
− σ min
τ abs = max
(3)
2
max
E a tensão normal média associada.
σ méd =
σ max + σ min
(4)
2
4- A tensão tangencial máxima, sobre qualquer plano que poderia ser passado através do ponto,
é a semidiferença entre a tensão principal máxima e mínima e atua sobre planos bissetrizes
entre os planos das tensões normais máximas e mínimas;
5- Quando existe um estado plano de tensões, uma das tensões principais é nula. Se os valores
de σ 1 e σ 2 têm o mesmo sinal, então a terceira tensão principal é zero, σ 3 = 0 .
6- A tensão tangencial máxima pode ser:
σ1 −σ2 σ1 −0
2
2
ou
σ2 −0
2
(5)
Dependendo da magnitude relativa e dos sinais das tensões principais.
7- Suponha que o material seja submetido a um estado de tensão plana, tal que as tensões no
plano sejam representadas como σ max e σ int , nas direções x’e y’, respectivamente; enquanto
a tensa fora do plano na direção z’é σ min = 0 , Figura 3.a. Os círculos de Mohr que
descrevem esse estado de tensão para as orientações do elemento em torno de cada eixo de
coordenadas são mostrados na Figura 3.b
3
Figura 3 - Elemento submetido a um estado plano de tensão.
Vê-se através da Figura 3 que apesar da tensão de cisalhamento máxima no plano ser
(τ x' y' )max = (σ max − σ int ) 2 , esse valor não representa a tensão de cisalhamento máxima absoluta à
qual o material está sujeito. Em vez disso, pela equação (3) , ou pela Figura 3.b, temos:
σ
− 0 σ máx
τ abs = (τ x' z' )max = max
=
max
2
2
(6)
Caso uma das tensões principais tenha o sinal contrário a da outra, as tensões serão
representadas por σ max e σ min e a tensão principal fora do plano por σ int = 0 . Os círculos de
Mohr que descrevem, o estado de tensão para as orientações do elemento em torno de cada eixo
de coordenadas são mostrados na Figura 4.b Neste caso:
τ abs = (τ x' y' )max = (σ max − σ min ) 2
(7)
max
Figura 4 - Elemento submetido a um estado plano de tensão.
4
Calcular a tensão de cisalhamento máxima absoluta, como ressaltado aqui, é importante quando se
projetam elementos feitos de material dúctil, visto que a resistência do material depende de sua
capacidade de suportar a tensão de cisalhamento .
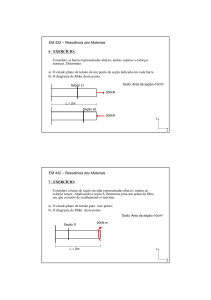
Exercícios:
1- Em virtude do carregamento aplicado, o elemento no ponto da estrutura da Figura 5.a está
sujeito ao estado plano de tensões mostrado. Determinar as tensões principais e a tensão de
cisalhamento máxima absoluta nesse ponto.
Figura 5. Elemento sujeito a um estado plano de tensões.
Resposta: σ max = 31,2 psi , σ int = 0 , σ min = −51,2 psi , τ abs = 41,2 psi , σ med = −10 psi
max
Figura 5- Resposta do exercício 1.
5
2- O ponto na superfície do vaso de pressão cilíndrico da Figura 6 está submetido a um estado
plano de tensões. Determinar a tensão de cisalhamento máxima absoluta nesse ponto.
Figura 7 – Vaso de Pressão.
τ abs = 16 MPa
max
σ méd = 16 MPa
Figura 6- Resposta do Exercício 2.
6
3- Desenhar os três círculos de Mohr que descrevem cada um dos seguintes estados de tensão .
Figura 7 – Paralelepípedos de Tensões.
Respostas:
a) σ max = 6 ksi , σ int = σ min = 0
b) σ max = 50 MPa σ int = 0 σ min = −40 MPa
c) σ max = 600 psi , σ int = 200 psi σ min = 100 psi
d) σ max = 0 , σ int = −7 ksi σ min = −9 ksi
e) σ max = σ int = σ min = −30 MPa
Referências Bibliográficas:
1. BEER, F.P. e JOHNSTON, JR., E.R. Resistência dos Materiais, 3.º Ed., Makron Books, 1995.
2. Gere, J. M. Mecânica dos Materiais, Editora Thomson Learning
3. HIBBELER, R.C. Resistência dos Materiais, 3.º Ed., Editora Livros Técnicos e Científicos, 2000.
Observações:
1- O presente texto é baseado nas referências citadas.
2- Todas as figuras se encontram nas referências citadas.
7