2. A TRIGONOMETRIA DO TRIÂNGULO RETÂNGULO Seja um

2. A TRIGONOMETRIA DO TRIÂNGULO RETÂNGULO
Seja um triângulo retângulo ABC de hipotenusa a e ângulos agudos B$ e C$ ,
opostos respectivamente aos catetos b e c (Figura 1).Sabemos do ensino fundamental
as definições:
$ é igual à razão entre o cateto oposto a B
$ e a hipotenusa, e é indicado
O seno de B
$ );
por sen ( B
$ é igual à razão entre o cateto adjacente a B
$ e a hipotenusa, e é
O cosseno de B
$ ).
indicado por cos ( B
$ é igual à razão entre o cateto oposto e o cateto adjacente a B
$ ,eé
A tangente de B
$ ).
indicada por tg ( B
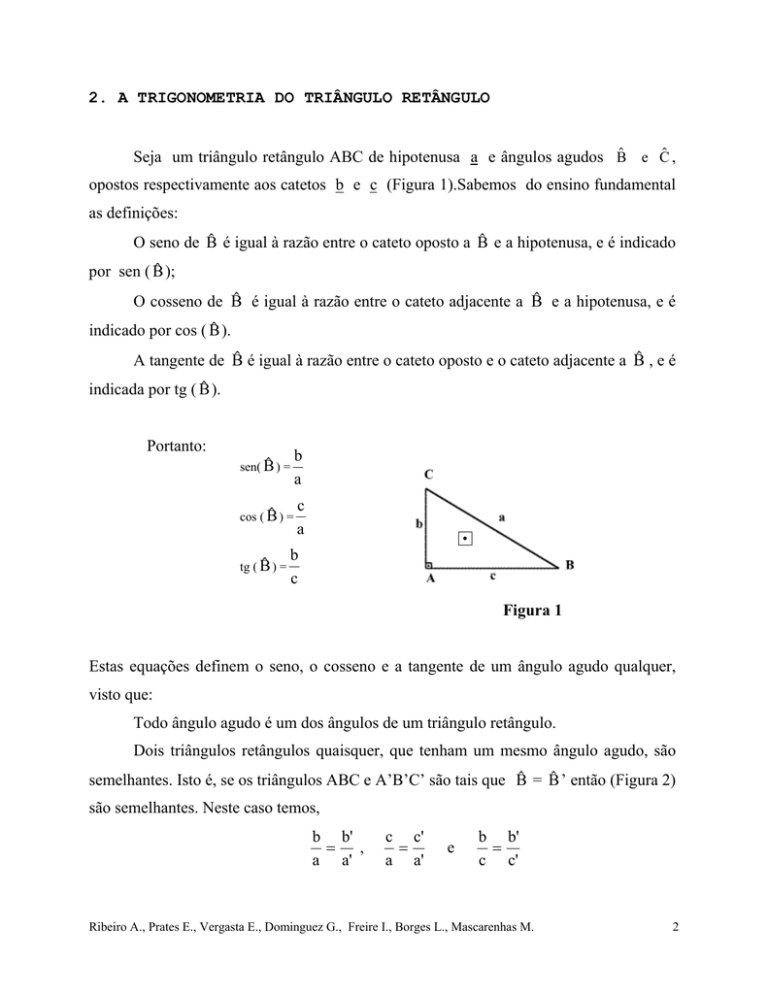
Portanto:
$ )=
sen( B
b
a
$ )=
cos ( B
c
a
$ )=
tg ( B
b
c
Figura 1
Estas equações definem o seno, o cosseno e a tangente de um ângulo agudo qualquer,
visto que:
Todo ângulo agudo é um dos ângulos de um triângulo retângulo.
Dois triângulos retângulos quaisquer, que tenham um mesmo ângulo agudo, são
$ =B
$ ’ então (Figura 2)
semelhantes. Isto é, se os triângulos ABC e A’B’C’ são tais que B
são semelhantes. Neste caso temos,
b b'
=
,
a a'
c c'
=
a a'
e
b b'
=
c c'
Ribeiro A., Prates E., Vergasta E., Dominguez G., Freire I., Borges L., Mascarenhas M.
2
$ ’ = sen B
$ , cos B
$ ’ = cos B
$ e tg B
$ ’ = tg B
$.
Logo, sen B
Portanto, o seno, o cosseno, e a tangente dependem apenas do ângulo agudo e não
do triângulo considerado .
Figura 2
$ e
Observemos que dado o triângulo retângulo ABC (figura 1), como b = a sen B
$ , então,
c = a cos B
$=
tg B
b a sen B̂ sen B̂
=
=
c a cos B̂
cosB̂
$ , cosseno de B
$ e tangente de B
$ são chamadas de funções
As funções seno de B
trigonométricas.
$ = b = cos Ĉ = cos (90 0 - B
$),
Observemos ainda que, sen B
a
isto é : o cosseno de um ângulo é o seno do ângulo do seu complementar, o que justifica a
denominação co-seno.
Como exemplo temos :
cos 30 0 = sen ( 90 0 - 30 0 ) = sen 60 0
cos 45 0 = sen (900 - 450 ) = sen 450 .
Ribeiro A., Prates E., Vergasta E., Dominguez G., Freire I., Borges L., Mascarenhas M.
3
A
Relação Fundamental
Dado um triângulo retângulo ABC (Figura 1), temos :
c2 b2 (b2 + c2 )
2
2
$
$
(cosB) + (senB) = 2 + 2 =
a
a
a2
Pelo Teorema de Pitágoras, c 2 + b 2 = a , chegamos então à seguinte relação,
chamada de relação fundamental:
$ + sen2 B
$ =1
cos2 B
Ribeiro A., Prates E., Vergasta E., Dominguez G., Freire I., Borges L., Mascarenhas M.
4