A. Funç˜oes trigonométricas directas

A. Funções trigonométricas directas
As funções seno, cosseno, tangente e cotangente são contı́nuas e
periódicas nos respectivos domı́nios. Todas elas são funções não
injectivas e, portanto, não possuem inversa.
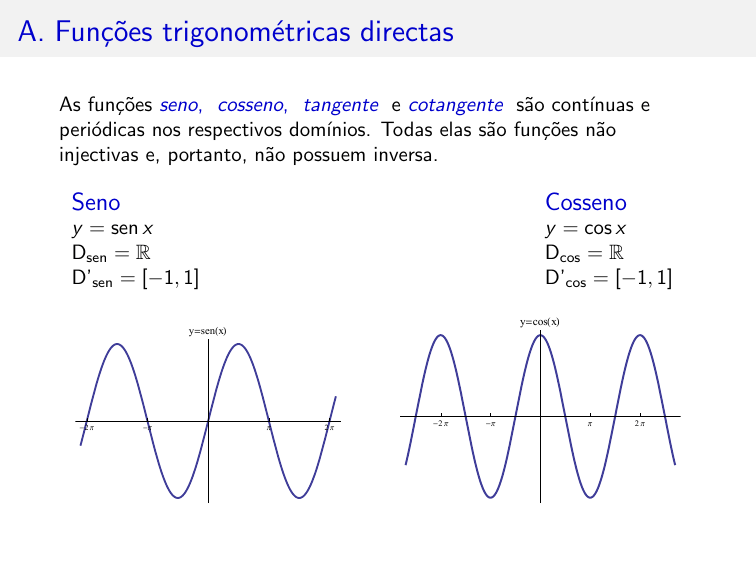
Seno
Cosseno
y = sen x
Dsen = R
D’sen = [−1, 1]
y = cos x
Dcos = R
D’cos = [−1, 1]
y=cosHxL
y=senHxL
-2 Π
-Π
Π
2Π
-2 Π
-Π
Π
2Π
Tangente
Cotangente
sen x
y = tg x =
cos x
π
Dtg = R\ 2 + kπ, k ∈ Z
D’tg = R
-2 Π
-Π
Π
y = cotg x =
cos x
sen x
Dcotg = R\{kπ, k ∈ Z}
D’cotg = R
2Π
-2 Π
-Π
Π
2Π
B. Funções trigonométricas inversas
Considerando restrições adequada das funções trigonométricas, obtemos
funções contı́nuas e bijectivas definidas em intervalos. A injectividade
será conseguida excluindo do domı́nio todos os pontos onde a função se
repete. A sobrejectividade será obtida eliminando do conjunto de
chegada todos os pontos que a função não assume. As inversas das
restrições assim definidas serão também contı́nuas.
B.1 Arco-seno
Relativamente à função seno, convencionamos considerar a restrição
bijectiva
h π πi
−→ [−1, 1]
sen : − ,
2 2
x
7−→ sen x .
A sua inversa, que se designa por arco-seno – lê-se arco (cujo) seno – é
a função
h π πi
arcsen : [−1, 1] −→ − ,
2 2
y
7−→ arcsen y ,
h π πi
cujo seno é igual
onde arcsen y indica o único arco do intervalo − ,
2 2
a y . Assim,
h π πi
x = arcsen y , y ∈ [−1, 1] ⇐⇒ y = sen x , x ∈ − ,
.
2 2
Π
2
-1
1
-
Π
2
y = arcsen x, x ∈ [−1, 1], D’arcsen = − π2 , π2
Pelo facto de sen e arcsen serem inversas uma da outra, tem-se
h π πi
,
arcsen (sen x) = x, ∀x ∈ − ,
2 2
sen (arcsen y ) = y , ∀y ∈ [−1, 1].
No entanto,
apesar
de fazer sentido calcular arcsen (sen z), para
z ∈ R\ − π2 , π2 , tem-se
h π πi
arcsen (sen z) 6= z , ∀z 6∈ − ,
,
2 2
uma vez que D’arcsen = − π2 , π2 .
Exemplo
π
(a) arcsen 1 = ,
√ 2
π
2
= ,
arcsen
2
4
√ !
3
π
arcsen −
=− .
2
3
h π πi
π π
π
onde o
,
e − são os únicos arcos do intervalo − ,
2 4
3
2 2
√
√
2
3
seno é, respectivamente, igual a 1 ,
e−
.
2
2
De facto,
(b) Tem-se, por exemplo,
sen (3π) = 0 e sen (8π) = 0,
mas arcsen 0 = 0.
h π πi
Porque 0 é o único arco do intervalo − ,
onde o seno é igual a 0 .
2 2
B.2 Arco-cosseno
Relativamente à função cosseno, convencionou-se considerar a restrição
bijectiva
cos : [0, π] −→ [−1, 1]
x
7−→ cos x .
A sua inversa, que se designa por arco-cosseno – lê-se arco (cujo)
cosseno – é a função
arccos :
[−1, 1] −→
y
7−→
[0, π]
arccos ,
onde arccos y indica o único arco do intervalo [0, π] cujo cosseno é igual
a y.
Assim,
x = arccos y , y ∈ [−1, 1] ⇐⇒ y = cos x , x ∈ [0, π] .
Π
-1
1
y = arccos x, x ∈ [−1, 1], D’arccos = [0, π]
Atendendo a que as funções cos e arccos são inversas uma da outra,
tem-se
arccos (cos x) = x , ∀x ∈ [0, π] ,
cos (arccos y ) = y , ∀y ∈ [−1, 1] .
Por outro lado, uma vez que D’arccos = [0, π], tem-se
arccos (cos z) 6= z , ∀z 6∈ [0, π] .
Exemplo
√ !
2
3π
(a) arccos 1 = 0 , arccos(−1) = π , arccos −
=
.
2
4
(b) arccos (cos 5π) = arccos(−1) = π!,
√
25π
2
π
arccos cos
= arccos
= .
4
2
4
B.3 Arco-tangente
Relativamente à função tangente, consideramos a restrição bijectiva
i π πh
−→ R
tg : − ,
2 2
x
7−→ tg x .
A sua inversa, designada por arco-tangente – lê-se arco (cuja) tangente
– é a função
i π πh
arctg : R −→ − ,
2 2
y 7−→ arctg y ,
i π πh
onde arctg y indica o único arco do intervalo − ,
cuja tangente é
2 2
igual a y .
Assim,
x = arctg y , com y ∈ R
se e só se
i π πh
y = tg x , x ∈ − ,
.
2 2
Π
2
-
Π
2
y = arctg x, x ∈ R, D’arctg = − π2 , π2
B.4 Arco-cotangente
Relativamente à função co-tangente, consideramos a restrição bijectiva
cotg :
]0, π[
x
−→
7−→
R
cotg x,
cuja inversa é a função arco-cotangente – lê-se arco (cuja) cotangente –
definida por
arccotg : R −→ ]0, π[
y 7−→ arccotg y ,
onde arccotg y indica o único arco do intervalo ]0, π[ cuja cotangente é
igual a y .
Assim,
x = arccotg y , com y ∈ R
se e só se
y = cotg x , x ∈ ]0, π[ .
Π
Π
2
y = arccotg x, x ∈ R, D’arccotg = ]0, π[
C. Funções hiperbólicas directas directas
Vamos agora introduzir as funções hiperbólicas, apresentar algumas das
suas propriedades e esboçar os seus gráficos. São funções que resultam
de combinações de exponenciais e possuem propriedades semelhantes,
do ponto de vista formal, às das funções trigonométricas.
e-x
1
ex
-1
-x
-e
C.1 Seno hiperbólico
O seno hiperbólico é a função
sh : R
−→
x
7−→
R
e x − e −x
.
2
Trata-se de uma função contı́nua, ı́mpar e estritamente crescente, logo
injectiva. Possui um único zero, a origem. Além disso,
lim sh x = +∞, lim sh x = −∞.
x→+∞
x→−∞
y=shHxL
y = sh x, x ∈ R, D’sh = R
C.2 Cosseno hiperbólico
O cosseno hiperbólico é a função
ch : R
−→
x
7−→
R
e x + e −x
.
2
Trata-se de uma função contı́nua e par. Logo, não é injectiva. Não
possui zeros e atinge um mı́nimo na origem, com valor ch 0 = 1. Além
disso, lim ch x = lim ch x = +∞.
x→+∞
x→−∞
y=shHxL
1
y = sh x, x ∈ R, D’sh = R
C.3 Tangente hiperbólica
A tangente hiperbólica é a função definida por
th : R
−→
x
7−→
R
sh x
,
ch x
ou seja, por
th x =
e x − e −x
,
e x + e −x
x ∈ R.
Trata-se de uma função contı́nua, ı́mpar e estritamente crescente, logo
injectiva. Possui um único zero, em 0. Além disso,
lim
x→+∞
1
1 − 2x
e x − e −x
e 2x − 1
e
th x = lim x
= lim 2x
= lim
= 1.
1
x→+∞ e + e −x
x→+∞ e
+ 1 x→+∞
1 + 2x
e
O gráfico da th possui, portanto, uma assı́mptota horizontal de equação
y = 1, para x → +∞. Da imparidade da th, existe outra assı́mptota
horizontal de equação y = −1, para x → −∞. Tem-se ainda
D’th = ] − 1, 1[ .
y
1
x
!1
y = th x, x ∈ R, D’th = ] − 1, 1[
C.4 Cotangente hiperbólica
A cotangente hiperbólica é a função definida por
coth : R\{0}
x
−→
7−→
R
ch x
,
sh x
ou seja, por
coth x =
e x + e −x
,
e x − e −x
x ∈ R\{0}.
Trata-se de uma função contı́nua, ı́mpar e sem zeros. Apesar de não ser
monótona, é estritamente decrescente para x > 0, onde toma valores
positivos, e para x < 0, onde toma valores negativos. Logo é injectiva.
Da definição sai que
lim coth x = +∞ ,
x→0+
lim
x→+∞
coth x = 1.
O gráfico da coth possui, portanto, uma assı́mptota horizontal de
equação y = 1, para x → +∞, e uma assı́mptota vertical de equação
x = 0. Da imparidade da coth , existe outra assı́mptota horizontal de
equação y = −1, para x → −∞. Tem-se ainda D’coth = R\[−1, 1] .
y
1
x
!1
y = coth x, x ∈ R\{0}, D’coth = R\[−1, 1]
C.5 Algumas propriedades
Com manipulações algébricas simples, é fácil verificar que estas funções
hiperbólicas verificam as seguintes propriedades:
(i) ch2 x − sh2 x = 1 ,
∀x ∈ R;
(ii) ch x + sh x = e x ,
∀x ∈ R;
(iii) sh(−x) = − sh x ,
(iv) ch(−x) = ch x ,
(v) th2 x +
∀x ∈ R;
∀x ∈ R;
1
=1,
ch2 x
(vi) coth2 x −
1
=1,
sh2 x
∀x ∈ R;
∀x ∈ R\{0};
(vii) sh(x + y ) = sh x ch y + ch x sh y ,
(viii) ch(x + y ) = ch x ch y + sh x sh y ,
∀x, y ∈ R;
∀x, y ∈ R;
Demonstração
(i) Seja x ∈ R, qualquer. Então
x
2 x
2
e + e −x
e − e −x
2
2
ch x − sh x =
−
2
2
=
1 2x
e + 2 + e −2x − e 2x + 2 − e −2x = 1.
4
(viii) Sejam x, y ∈ R, quaisquer. Então
ch x ch y + sh x sh y =
=
e x +e −x
2
·
e x+y +e x−y +e −x+y +e −x−y
4
=
e x+y +e −x−y
2
e y +e −y
2
+
+
e x −e −x
2
·
e y −e −y
2
e x+y −e x−y −e −x+y +e −x−y
4
= ch(x + y ).
As restantes alı́neas demonstram-se de maneira semelhante.
D. Funções hiperbólicas inversas
Vamos agora definir as funções hiperbólicas inversas. Como vimos na
subsecção C, as funções sh, th e coth são injectivas, enquanto que a
função ch não é injectiva e, portanto, não será invertı́vel. Para esta
última, iremos considerar uma restrição apropriada.
D.1 Argumento do seno hiperbólico
A função sh é contı́nua, bijectiva e possui inversa contı́nua. Trata-se da
função argumento do seno hiperbólico, que se define por
argsh : R
y
−→
7−→
R
argsh y ,
onde
x = argsh y , y ∈ R ⇐⇒ y = sh x , x ∈ R.
Mas, para x ∈ R , tem-se
y = sh x
⇐⇒
⇐⇒
e x − e −x
2
e 2x − 1
⇐⇒ e 2x − 2ye x − 1 = 0.
y=
2e x
y=
A última condição em (1) traduz uma equação do segundo grau na
incógnita e x . Tratando-a com a fórmula resolvente, sai
p
ex = y ± y 2 + 1 ,
sendo a solução com o sinal + a única admissı́vel, uma vez que
p
e x > 0 , ∀x ∈ R
e
y − y 2 + 1 < 0 , ∀y ∈ R.
Mas
ex = y +
donde
p
p
y 2 + 1 ⇐⇒ x = log y + y 2 + 1 ,
p
argsh y = log y + y 2 + 1 ,
∀y ∈ R.
Assim, a função argsh fica completamente definida.
(1)
D.2 Argumento do cosseno hiperbólico
A função ch não é injectiva, logo, não é invertı́vel. Como tal,
definiremos a inversa da seguinte restrição bijectiva e contı́nua
ch :
[0, +∞[
x
−→
7−→
[1, +∞[
ch x,
que se designa por argumento do cosseno hiperbólico e que é também
uma função contı́nua. Representa-se por
argch :
[1, +∞[
y
−→
7−→
[0, +∞[
argch y ,
onde
x = argch y , y ∈ [1, +∞[ ⇐⇒ y = ch x , x ∈ [0, +∞[ .
Mas, para x ≥ 0 , tem-se
y = ch x
⇐⇒
⇐⇒
e x + e −x
2
e 2x + 1
y=
⇐⇒ e 2x − 2ye x + 1 = 0.
2e x
y=
(2)
A última igualdade de traduz uma equação do segundo grau em e x ,
donde
p
ex = y ± y 2 − 1 .
Como x ≥ 0 =⇒ e x ≥ 1, a solução com o sinal + é a única admissı́vel (a
solução com o sinal − corresponderia à inversa da restrição do ch para
x ≤ 0). Mas
ex = y +
p
y 2 − 1 , x ≥ 0 , y ≥ 1 ⇐⇒ x = log
donde
argch y = log
y+
p
y2 − 1
p
y + y 2 − 1 , x ≥ 0 , y ≥ 1,
, y ∈ [1, +∞[ ,
ficando a função argumento do cosseno hiperbólico completamente definida.
D.3 Argumento da tangente hiperbólica
A função tangente-hiperbólica é injectiva mas não é sobrejectiva. Para
poder inverter, basta considerar
th : R
x
−→
7−→
] − 1, 1[
th,
que é bijectiva e, portanto, é invertı́vel. Sendo contı́nua num intervalo, a
sua inversa é contı́nua. Trata-se da função argumento da tangente
hiperbólica, que se define por
argth :
] − 1, 1[
y
−→
7−→
R
argth y ,
onde
x = argth y , y ∈ ] − 1, 1[ ⇐⇒ y = th x , x ∈ R.
Para x ∈ R , y ∈ ] − 1, 1[ , tem-se
y = th x
⇐⇒
y=
e x − e −x
e 2x − 1
⇐⇒ y = 2x
x
−x
e +e
e +1
s
⇐⇒
e
2x
(1 − y ) = 1 + y ⇐⇒ x = log
donde
s
argth y = log
1+y
1−y
1+y
1−y
!
, y ∈ ] − 1, 1[ ,
completando-se a definição do argumento da tangente hiperbólica.
!
,
D.4 Argumento da cotangente hiperbólica
A função cotangente-hiperbólica é injectiva mas não é sobrejectiva.
Consideremos então
coth : R\{0}
x
−→
7−→
R\ [−1, 1]
coth
que é bijectiva e, portanto, é invertı́vel. A sua inversa é contı́nua.
Trata-se da funçãoargumento da cotangente hiperbólica, que se define
por
argcoth : R\ [−1, 1] −→ R\{0}
y
7−→ argcoth y
onde
x = argcoth y , y ∈ R\ [−1, 1] ⇐⇒ y = coth x , x ∈ R\{0}.
Para x ∈ R\{0} , y ∈ R\ [−1, 1] , tem-se
s
y = coth x ⇐⇒ x = log
y +1
y −1
!
,
pelo que
s
argcoth y = log
y +1
y −1
!
, y ∈ R \ [−1, 1],
ficando assim completa a definição da função argumento da cotangente
hiperbólica.