Revisão de Matemática Aplicada (Unidades e

MAT03301 - MATEMÁTICA APLICADA
Professor: Filipe Arantes Fernandes
Aluno: _____________________________________
Data: _____/_____/ 2017
EXERCÍCIOS DE REVISÃO:
UNIDADES DE MEDIDAS E POLÍGONOS
Polígonos
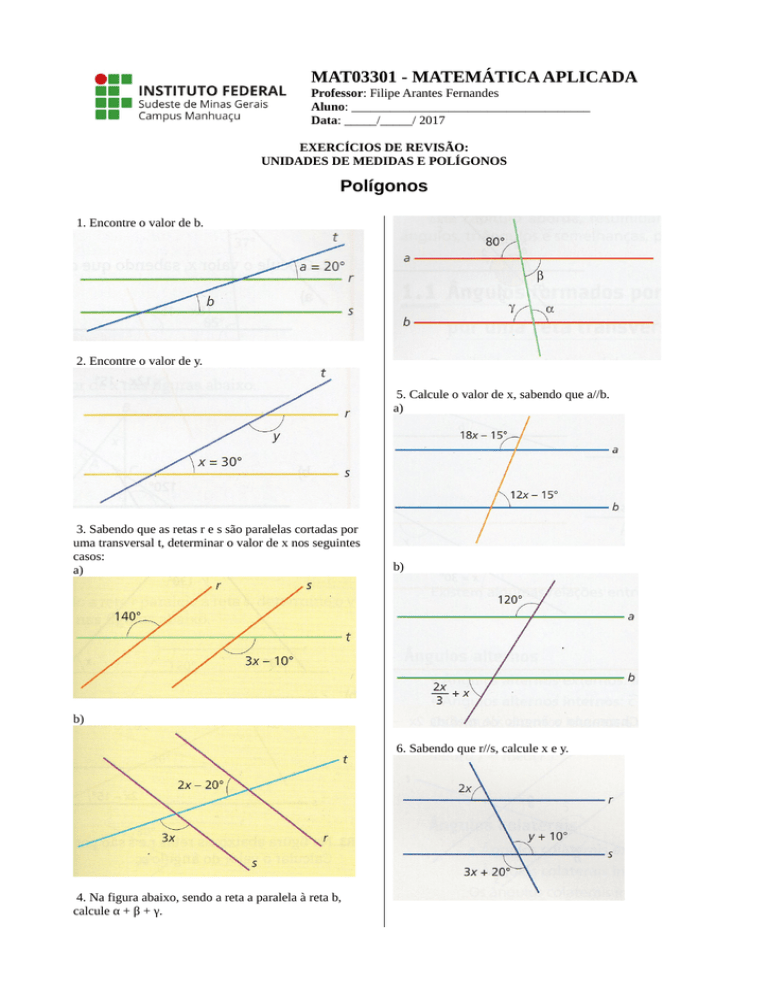
1. Encontre o valor de b.
2. Encontre o valor de y.
5. Calcule o valor de x, sabendo que a//b.
a)
3. Sabendo que as retas r e s são paralelas cortadas por
uma transversal t, determinar o valor de x nos seguintes
casos:
a)
b)
b)
6. Sabendo que r//s, calcule x e y.
4. Na figura abaixo, sendo a reta a paralela à reta b,
calcule α + β + γ.
7. Na figura abaixo, os ângulos têm os lados
respectivamente paralelos (AB // A’B’ e AC//A’C’).
Calcular o valor de x.
11. Determine o valor de x e y, sendo r paralela a s.
12. Sendo a reta r paralela à reta s, determine o valor de α
nas figuras abaixo.
a)
8. Sabendo que os ângulos têm os lados respectivamente
paralelos, calcule o valor de x.
b)
9. Sendo r e s paralelas, determine os valores de x e y nos
cados abaixo.
a)
b)
10. Na figura abaixo, as retas r e s são paralelas. Calcular
o valor do ângulo α.
c)
13. Calcule o valor de x nas figuras abaixo.
a)
b)
c)
16. Determine o valor dos ângulos x e y na figura abaixo.
17. Determine o valor de x em cada triângulo.
a)
b)
14. Determine o valor do ângulo x no triângulo ABC.
18. Sabendo que o triângulo ABC é equilátero, determine
x e y.
15. Determine o valor de x nos triângulos.
a)
19. O perímetro (soma dos lados) de um triângulo
equilátero é 105 cm. Determine o valor de cada lado.
20. Sendo o perímetro de um triângulo isósceles 150 cm
e sabendo que a base mede 30 cm, calcule a medida dos
outros lados.
b)
21. Sabendo que os triângulos ABC são isósceles de base
BC, determine x.
a)
b)
22. Determine o valor do ângulo e no triângulo abaixo:
23. Determine o valor de x.
a)
b)
c)
25. Determine o valor de x no triângulo abaixo.
b)
26. Determine o valor de x e y.
24. Sabendo que o triangulo ABC é isósceles, sendo BC
sua base, determine o valor de x nos seguintes casos.
a)
27. Sabendo que o triângulo ABC é isósceles de base BC,
determine o valor de x e y nos seguintes casos.
a)
b)
e)
29. Sendo a paralela a b, então o valor de x é:
28. Determine o valor de x nos casos a seguir.
a)
30. Considere as retas r, s, t, e u todas num mesmo plano,
com r // u. O valor em grau de 2x + 3y é:
b)
c)
d)
31. Se as retas r e s da figura são paralelas, então 3α + β
vale:
32. Na figura, a=100º e b=110º. Quanto mede o ângulo
x?
33. Na figura, a medida x do ângulo assinalado é:
36. Na figura, BC = CA = AD = DE. O ângulo CÂD
mede:
34. Dois lados de um triangulo isósceles medem,
respectivamente, 5 cm e 2 cm. Qual é o seu perímetro?
35. Na figura, AC = CB = BD e  = 25º. O ângulo x
mede:
Unidades de Medidas
37. Transforme:
c) 2,14 m² em mm²
a) 2 km em m
e) 125,8 m² em km²
b) 1,5 m em mm
f) 12,9 km² em m²
c) 5,8 km em cm
g) 15,3 m² em mm²
d) 0,4 m em mm
h) 2,5 mm² em m²
e) 27 mm em cm
39. Converta as áreas de volume:
f) 126 mm em m
a) 8,132 km3 em hm3
g) 12 m em km
b) 180 hm3 em km3
h) 10500 mm em cm
c) 1 m3 em mm3
i) 2,5 m em cm
d) 5 cm3 em m3
38. Converta as unidades de área:
e) 78,5 m3 em km3
a) 8,37 dm² em mm²
f) 12 m3 em cm3
b) 3,1416 m² em cm²
g) 139 mm3 em m3