Superfície Equação Superfície Equação 1 x y z a b c + + = −Todos
Propaganda
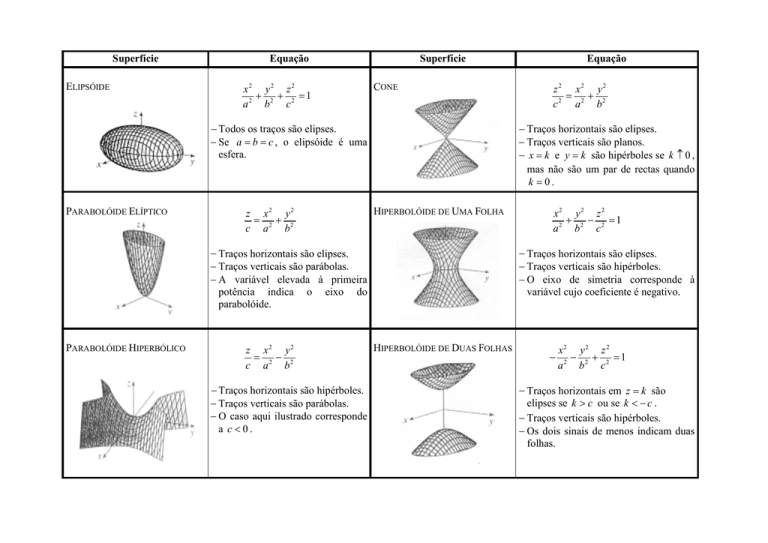
Superfície ELIPSÓIDE Equação x2 y 2 z 2 + + =1 a 2 b2 c 2 Superfície CONE − Todos os traços são elipses. − Se a = b = c , o elipsóide é uma esfera. PARABOLÓIDE ELÍPTICO z x2 y 2 = + c a 2 b2 z x2 y2 = − c a2 b2 − Traços horizontais são hipérboles. − Traços verticais são parábolas. − O caso aqui ilustrado corresponde a c <0. z 2 x2 y2 = + c2 a2 b2 − Traços horizontais são elipses. − Traços verticais são planos. − x = k e y = k são hipérboles se k ≠ 0 , mas não são um par de rectas quando k =0. HIPERBOLÓIDE DE UMA FOLHA x2 y 2 z 2 + − =1 a 2 b2 c 2 − Traços horizontais são elipses. − Traços verticais são hipérboles. − O eixo de simetria corresponde à variável cujo coeficiente é negativo. − Traços horizontais são elipses. − Traços verticais são parábolas. − A variável elevada à primeira potência indica o eixo do parabolóide. PARABOLÓIDE HIPERBÓLICO Equação HIPERBOLÓIDE DE DUAS FOLHAS − x2 y2 z 2 − + =1 a2 b2 c2 − Traços horizontais em z = k são elipses se k > c ou se k < − c . − Traços verticais são hipérboles. − Os dois sinais de menos indicam duas folhas.
