Aula 1. Progressões Aritméticas

2◦ Ano
Recuperação Paralela
Aluno:
Código:
Turma:
Data:
/
/
Aula 1. Progressões Aritméticas
Definição e Classificação
Progressão Aritmética (PA) é uma sequência onde
a diferença entre cada termo (a partir do segundo) e o
termo anterior é constante. Essa diferença constante (número fixo) é denominada razão da progressão, usualmente representada por r. Assim, cada termo de uma PA
é obtido do anterior somando-se a razão: para qualquer
n ≥ 2, tem-se que an = an−1 + r .
Uma PA pode ser classificada em crescente, se r > 0;
decrescente, se r < 0; ou constante, se r = 0.
2. Complete a sequência abaixo, sabendo que ela é
uma PA.
( 3 ;
; 4, 2 ;
; 5, 4 ;
)
Propriedades
P1 Sempre podemos escrever os termos de uma PA em
função do primeiro termo a1 e da razão r:
(a1 , a1 + r , a1 + 2r , a1 + 3r , · · · , a1 + (n − 1)r , · · · )
|{z} | {z } | {z }
| {z }
a2
a3
a4
3. Numa PA, em que a1 + a15 = 48, calcule:
(a) a2 + a14
an
Dessa forma, afirmamos que o termo geral de uma
PA pode ser dado por:
an = a1 + (n − 1) · r
P2 Numa PA, cada termo, a partir do segundo, é igual
à média aritmética entre o termo anterior e o posterior na sequência:
an =
(b) a3 + a5 + a11 + a13
an−1 + an+1
2
P3 Numa PA qualquer (r , 0), temos que
am + an = ap + aq ⇐⇒ m + n = p + q
P4 Numa PA, indicamos por Sn a soma de seus n primeiros termos. Como a1 + an = a2 + an−1 = · · · , podemos encontrar Sn pela expressão
Sn =
(c) a8
(a1 + an ) · n
2
Atividades
1. (UERGS) O 13◦ termo da progressão aritmética
(−83, −78, −73, · · · ) é:
4. Numa PA, com a1 = −5 e razão r = 4, calcule a soma
dos 20 primeiros termos.
(a) −43
(b) −38
(c) −33
(d) −28
(e) −23
Professor Podô
[email protected]
1
Recuperação Paralela
5. (UFPA) Sabendo que a sequência (1−3x, x−2, 2x+1)
é uma PA, determine o valor de x.
2◦ Ano
Tarefa
Em uma folha separada, resolva o exercício 40
da página 161 do seu livro didático. Não é necessário copiar o enunciado do exercício. Não se
esqueça de colocar seu nome, código e sala em
sua folha e entregá-la ao professor na próxima
semana.
(a) −2
(b) 0
(c) 2
(d) 4
(e) 6
6. (Mackenzie) Um atleta, treinando para uma maratona, corre 15km no primeiro dia e aumenta o seu
percurso de 500m a cada dia. Depois de 61 dias consecutivos de treinamento, o atleta terá percorrido:
(a) 1400km
(b) 1420km
(c) 1760km
(d) 1830km
(e) 2560km
7. (UFRR-RR) Para atender a demanda dos consumidores, um supermercado iniciou a venda de pequenas cestas natalinas um mês antes do Natal. No primeiro dia, foram colocadas à venda 15 cestas, no
segundo, 20 cestas, no terceiro, 25 cestas, e assim
sucessivamente, até o trigésimo dia (véspera do Natal), e todas foram vendidas. O total de cestas de
Natal vendidas pelo supermercado foi de:
(a) 815
(b) 935
(c) 1500
(d) 2625
(e) 2800
.
Professor Podô
[email protected]
2
2◦ Ano
Recuperação Paralela
Aluno:
Código:
Turma:
Data:
/
/
Aula 2. Progressões Geométricas
Definição e Classificação
Progressão Geométrica (PG) é uma sequência onde o
quociente da divisão de cada termo (a partir do segundo)
pelo termo anterior é constante. Esse quociente constante
(número fixo) é denominado razão da progressão, usualmente representada por q. Assim, cada termo de uma PG,
a partir do segundo, é obtido do anterior multiplicandose um número fixo (a razão). Ou seja, para qualquer n ≥ 2,
a
tem-se n = q, portanto, an = an−1 · q.
an−1
Uma PG pode ser:
• Crescente, se q > 0 e os termos forem positivos ou
se 1 > q > 0 e os termos forem negativos;
P5 Numa PG em que −1 < q < 1, quando n cresce, an
aproxima-se de zero, daí qn tamb[em se aproxima
de zero. Assim, podemos dizer que a soma de infinitos termos de PGs nessas condições pode ser calculada pela expressão
S∞ =
a1
1−q
Atividades
1
1
é
1. O número de termos da PG 1, , · · · ,
2
64
(a) 5
(b) 6
• Decrescente, se 1 > q > 0 e os termos forem positivos ou q > 0 e os termos forem negativos;
(c) 7
(d) 8
• Constante, se q = 0; ou
(e) 9
• Alternante, se q < 0.
Propriedades
P1 Sempre podemos escrever os termos de uma PG em
função do primeiro termo a1 e da razão q:
(a1 , a1 · q , a1 · q2 , a1 · q4 , · · · , a1 · qn−1 , · · · )
|{z} |{z} |{z}
| {z }
a2
1
, a2 , a3 , a4 , a5 , 864 é uma
9
progressão geométrica, a razão é um número:
a3
a4
(a) primo.
(b) quadrado perfeito.
an
Dessa forma, afirmamos que o termo geral de uma
PG pode ser dado por:
an = a1
2. (Ufor/CE) Se a seqüência
· qn−1
(c) divisível por 3.
(d) múltiplo de 4.
(e) divisível por 9.
P2 Numa PG qualquer (q , 0), temos que o produto de
termos equidistantes é sempre igual, isto é,
am · an = ap · aq ⇐⇒ m + n = p + q
P3 Dados três termos consecutivos an−1 , an , an+1 de
uma PG, o quadrado do termo central é igual ao
produto dos outros dois:
a2n = an−1 · an+1
3. (Fuvest) O quinto e o sétimo termos de uma PG de
razão positiva valem, respectivamente, 10 e 16. O
sexto termo dessa PG é:
(a) 13
√
(b) 10 6
(c) 4
P4 Numa PG, indicamos por Sn a soma de seus n primeiros termos. Como a1 · an = a2 · an−1 = · · · , podemos encontrar Sn pela expressão
Sn =
Professor Podô
√
(d) 4 10
(e) 10
a1 (1 − qn )
1−q
[email protected]
1
Recuperação Paralela
4. (Acafe/SC - adaptado) Uma certa epidemia, causada
por um vírus, atingiu uma cidade. No primeiro dia
foram registrados 60 casos, no segundo dia 180 novos casos, no terceiro, 540 e nos dias subsequentes o
número de novos casos se manteve na mesma progressão. A estimativa para ocorrência de 14.580 novos casos se dará no:
2◦ Ano
Tarefa
Em uma folha separada, resolva o exercício 84
da página 166 do seu livro didático. Não é necessário copiar o enunciado do exercício. Não se
esqueça de colocar seu nome, código e sala em
sua folha e entregá-la ao professor na próxima
semana.
(a) 8◦ dia
(b) 5◦ dia
(c) 7◦ dia
(d) 6◦ dia
(e) 10◦ dia
5. O lado de um triângulo eqüilátero mede 3m.
Unindo-se os pontos médios de seus lados, obtémse um novo triângulo eqüilátero. Unindo-se os pontos médios do novo triângulo, obtém-se outro triângulo eqüilátero e, assim sucessivamente. Determine
a soma dos perímetros de todos os triângulos construídos.
6. (UEPA) Um carro, cujo preço à vista é R$24000, 00,
pode ser adquirido dando-se uma entrada e o restante em 5 parcelas que se encontram em progressão geométrica. Um cliente que optou por esse
plano, ao pagar a entrada, foi informado que a segunda parcela seria de R$4000, 00 e a quarta parcela de R$1000, 00. Quanto esse cliente pagou de
entrada na aquisição desse carro?
.
Professor Podô
[email protected]
2
2◦ Ano
Recuperação Paralela
Aluno:
Código:
Turma:
Data:
/
/
Aula 3. Problemas de Contagem
Introdução
Atividades
Problemas de contagem são, muitas vezes, considerados difíceis entre alunos e professores, apesar de as técnicas matemáticas necessárias serem bastante elementares: apenas o conhecimento das operações aritméticas de
soma, subtração, multiplicação e divisão.
Para resolver esses problemas, portanto, basta
habituar-se a trabalhar com problemas de contagem e a
ver que, afinal de contas, tais problemas podem ser resolvidos com raciocínios simples na grande maioria dos
casos, sem exigir o uso de fórmulas complicadas.
1. Um restaurante possui um cardápio que apresenta
escolhas de saladas (salada verde, salada russa ou
salpicão), sopas (caldo verde, canja ou de legumes)
e pratos principais (bife com fritas, peixe com puré,
frango com legumes ou lasanha).
(a) De quantos modos se pode escolher um prato
deste cardápio?
Princípio Fundamental da Contagem
O Princípio Fundamental da Contagem é diz, simplesmente, o seguinte:
Se uma decisão A pode ser tomada de n modos
e, qualquer que seja essa escolha, uma outra decisão B pode ser tomada de m modos, então o
número de maneiras de se tomarem consecutivamente as decisões A e B é igual a n · m.
O Princípio Multiplicativo pode ser aplicado, também, quando temos diversas etapas de decisão: desde que
o número de possibilidades em cada etapa não dependa
das decisões anteriores, basta multiplicá-los para achar o
número total de possibilidades.
A estratégia para resolver problemas de contagem é:
(b) De quantos modos se pode escolher uma refeição completa, formada por uma salada, uma
sopa e um prato principal?
2. Existem duas vias de locomoção de uma cidade A
para uma cidade B e três vias de locomoção da cidade B a uma cidade C. De quantas maneiras se
pode ir de A a C, passando por B?
• Postura: devemos sempre nos colocar no papel da
pessoa que deve fazer a ação solicitada pelo problema e ver que decisões devemos tomar.
• Divisão: devemos, sempre que possível, dividir as
decisões a serem tomadas em decisões mais simples, correspondentes às diversas etapas do processo de decisão. Mas atenção: a ordem em que as
decisões são tomadas pode ser extremamente importante para a simplicidade do processo de resolução.
3. Numa lanchonete, há cinco tipos de sanduíches,
quatro tipos de refrigerante e três tipos de sorvete.
De quantas maneiras podemos tomar um lanche
composto de um sanduíche, um refrigerante e um
sorvete?
• Restrições: pequenas dificuldades adiadas costumam se transformar em imensas dificuldades. Se
uma das decisões a serem tomadas for mais restrita
que as demais, essa é a decisão que deve ser tomada
em primeiro lugar.
Muitas vezes pode ser útil fazer um esquema da situação para exibir as possibilidades de contagem.
Professor Podô
[email protected]
1
Recuperação Paralela
4. De quantas maneiras uma família de cinco pessoas
pode sentar-se num banco de cinco lugares para tirar uma foto?
2◦ Ano
Tarefa
Em uma folha separada, resolva o exercício 6 da
página 476 do seu livro didático. Não é necessário copiar o enunciado do exercício. Não se
esqueça de colocar seu nome, código e sala em
sua folha e entregá-la ao professor na próxima
semana.
5. Um clube tem trinta membros. A diretoria é formada por um presidente, um vice-presidente, um
secretário e um tesoureiro. Se uma pessoa pode
ocupar apenas um desses cargos, de quantas maneiras é possível formar uma diretoria?
6. As placas dos automóveis são formadas por três letras seguidas de quatro algarismos. Quantas placas
podemos criar com as letras A e B e os algarismos
pares, podendo repetir a letra e não podendo repetir o algarismo?
.
Professor Podô
[email protected]
2
2◦ Ano
Recuperação Paralela
Aluno:
Código:
Turma:
Data:
/
/
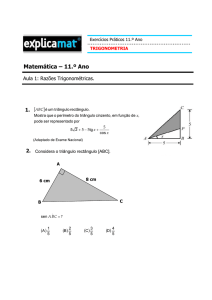
Aula 4. Trigonometria no Triângulo Retângulo
Definição
Atividades
A trigonometria é o estudo das relações entre lados e
ângulos nos triângulos retângulos. Considere o triângulo
retângulo a seguir.
1. Em cada triângulo a seguir, determine o valor do
seno, cosseno e tangente dos ângulos α indicados.
(a)
Todos os triângulos retângulos que têm mesmos ângulos internos são semelhantes a este. As razões de semelhança são chamadas de:
• Seno:
sen x =
medida do cateto oposto a x CO
=
medida da hipotenusa
hip
• Cosseno:
medida do cateto adjacente a x CA
cos x =
=
medida da hipotenusa
hip
(b)
• Tangente:
medida do cateto oposto a x
CO
tg x =
=
medida do cateto adjacente a x CA
Assim, por exemplo, no triângulo anterior, temos:
b
a
c
• cos B̂ =
a
• sen B̂ =
• tg B̂ =
(c)
b
c
Lembre-se que estamos trabalhando com triângulos
retângulos, logo o teorema de pitágoras continua valendo:
a2 = b 2 + c 2
Trigonometria dos ângulos notáveis
2. Um foguete é lançado sob um ângulo de 45° em relação ao solo. Supondo que sua trajetória seja retilínea, qual sua altura quando ele percorreu 4 km?
Ao dividirmos um quadrado ou um triângulo equilátero por uma diagonal ou uma altura, respectivamente,
encontraremos os ângulos de 30◦ , 45◦ e 60◦ . Esses ângulos são chamados de notáveis e, usando as relações definidas, podemos encontrar os seguintes valores:
seno
cosseno
tangente
Professor Podô
30◦
45◦
60◦
1
√2
3
√2
3
3
2
√2
2
2
3
2
1
2
√
1
√
√
3
[email protected]
1
Recuperação Paralela
3. A figura a seguir representa uma árvore de altura
12m. Calcule a sombra s quando um raio luminoso
forma com o solo um ângulo de 60◦ .
2◦ Ano
Tarefa
Em uma folha separada, resolva o exercício 14
da página 219 do seu livro didático. Não é necessário copiar o enunciado do exercício. Não se
esqueça de colocar seu nome, código e sala em
sua folha e entregá-la ao professor na próxima
semana.
4. Um observador O de altura 1, 75m vê um balão B
sob ângulo de 30◦ em relação ao solo. Em determinado instante, a distância do observador ao balão é
de 146, 50m. Nessas condições:
(a) Desenhe uma figura esquematizando a situação.
(b) Determine a altura h do balão em relação ao
solo.
5. (UFAM-AM) Se um cateto e a hipotenusa de um triângulo retângulo medem 2a e 4a, respectivamente,
então a tangente do ângulo oposto ao menor lado é:
.
Professor Podô
[email protected]
2
2◦ Ano
Recuperação Paralela
Aluno:
Código:
Turma:
Data:
/
/
Aula 5. Relações Trigonométricas
Funções Trigonométricas
Essas últimas podem ser obtidas a partir das primeiras, por isso podem ser chamadas de relações trigonométricas secundárias.
Definir as funções trigonométricas, a nível de ensino médio, é, essencialmente, apenas uma formalização
Em geral, as relações trigonométricas são utilizadas
maior em torno do que já se deve ter visto, agora sob o
para simplificar expressões que envolvem diversas funponto de vista das funções. As três funções trigonométrições trigonométricas.
cas principais são:
• Função seno: é a função real que a cada x ∈ R associa
o valor real sen x;
• Função cosseno: é a função real que a cada x ∈ R
associa o valor real cos x;
• Função tangente: é a função real que a cada x ∈ R,
x , π2 + kπ, k ∈ Z, associa o valor real tg x.
Atividades
1. Determine os valores das demais funções trigonométricas de um arco x quando:
(a) sen x = −
π
1 3π
e
<x<
2
2
2
(b) cos x = −
π
2
e0<x<
5
2
Há outras três funções trigonométricas “secundárias”,
definidas a partir das anteriores:
• Função secante: é a função real que a cada x ∈ R,
1
;
x , π2 + kπ, k ∈ Z, associa o valor real
cos x
• Função cossecante: é a função real que a cada x ∈ R,
1
x , kπ, k ∈ Z, associa o valor real
;
sen x
• Função tangente: é a função real que a cada x ∈ R,
1
x , π2 + kπ, k ∈ Z, associa o valor real
.
tg x
Relações Trigonométricas
As relações entre os valores das funções trigonométricas de um mesmo arco são denominadas relações trigonométricas. As relações trigonométricas fundamentais são
as seguintes:
• sen2 x + cos2 x = 1 , para todo x ∈ R;
• tg x =
sen x
, para todo x ,
cos x
π
2
+ kπ, k ∈ Z.
Graças a essas relações entre as funções trigonométricas, conseguimos calcular as todas as funções se apenas
uma delas for dada.
Além dessas, existem outras relações fundamentais:
• sen2 x = 1 − cos2 x , para todo x ∈ R;
• cos2 x = 1 − sen2 x , para todo x ∈ R;
• cotg x =
Professor Podô
1
cos x
=
, para todo x , kπ, k ∈ Z.
tg x sen x
[email protected]
1
2◦ Ano
Recuperação Paralela
1
π
, com 0 < x < , determine o valor
4
2
de sec x + cosec x.
2. Dado cos x =
(c) y =
cotg x + cosec x
x
sen
3. Simplifique as expressões:
(a) y = cos x · tg x · cosec x
(d) .
y = (sen x − cos x) · (cosec x − sen x) · (tg x − cotg x)
(b) y =
sec x − cosec x
1 − cotg x
Tarefa
Em uma folha separada, resolva o exercício 46
da página 247 do seu livro didático. Não é necessário copiar o enunciado do exercício. Não se
esqueça de colocar seu nome, código e sala em
sua folha e entregá-la ao professor na próxima
semana.
Professor Podô
[email protected]
2
2◦ Ano
Recuperação Paralela
Aluno:
Código:
Turma:
Data:
/
/
Aula 6. Porcentagem
2. (Fuvest) (10%)2 =
Definição
Porcentagem é uma fração de denominador centesimal, ou seja, é uma fração de denominador 100. Representamos a porcentagem pelo símbolo % e lemos “por
20
cento”. Deste modo, a fração
é uma porcentagem
100
que podemos representar por 20%.
É comum representarmos uma porcentagem na forma
decimal, por exemplo, 75% na forma decimal seria representado por 0, 75.
Para calcularmos uma porcentagem p% de um valor
p
por V :
V , basta multiplicarmos a fração
100
p
p% de V =
·V
100
Em muitos casos, resolver problemas envolvendo porcentagens resume-se a montar e resolver uma regra de
três simples.
(a) 100%
(b) 20%
(c) 5%
(d) 1%
(e) 0, 1%
3. (Puc 2010) Em uma turma de Ciências da Computação formada de 40 rapazes e 40 moças, tem-se a
seguinte estatística: 20% dos rapazes são fumantes
e 30% das moças são fumantes. Logo, a porcentagem dos que não fumam na turma é:
(a) 25%
Atividades
1. (Enem) Um professor dividiu a lousa da sala de aula
em quatro partes iguais. Em seguida, preencheu
75% dela com conceitos e explicações, conforme a
figura seguinte.
Algum tempo depois, o professor apagou a lousa
por completo e, adotando um procedimento semelhante ao anterior, voltou a preenchê-la, mas, dessa
vez, utilizando 40% do espaço dela. Uma representação possível para essa segunda situação é
(b) 50%
(c) 60%
(d) 65%
(e) 70%
4. (Puc 2012) Em março de 2011, a garrafa de 500ml
de suco de bujurandu custava R$5, 00. Em abril, o
valor subiu 10% e, em maio, caiu 10%. Qual o preço
da garrafa em junho?
(a) R$4, 50
(b) R$4, 95
(c) R$5, 00
(d) R$5, 50
(e) R$6, 00
Professor Podô
[email protected]
1
Recuperação Paralela
5. (Fuvest) Na reprodução de uma figura, a primeira
cópia obtida reduziu em 30% a área desta figura.
A seguir, esta cópia foi reproduzida com ampliação
de 40%. A área da figura obtida na segunda cópia,
comparada com a área da figura original, é:
2◦ Ano
Tarefa
Em uma folha separada, resolva o exercício 34
da página 176 do seu livro didático. Não é necessário copiar o enunciado do exercício. Não se
esqueça de colocar seu nome, código e sala em
sua folha e entregá-la ao professor na próxima
semana.
(a) 98% menor
(b) 90% maior
(c) exatamente igual
(d) 90% maior
(e) 2% menor
6. (UTFPr 2012) As vendas de imóveis em uma cidade
foram, em 2008, 60% superior às vendas de 2007.
Da mesma forma, podemos então afirmar que as
vendas de imóveis desta mesma cidade foram, em
2007, x% inferior às vendas de 2008. Determine x.
(a) 37%.
(b) 40%.
(c) 55, 5%.
(d) 62, 5%.
(e) 60%.
7. (Puc 2013) O salário de Paulo sofreu um desconto
total de 8%; com isso, ele recebeu R$1.518, 00.
O valor bruto do salário de Paulo é:
(a) R$1.390, 00
(b) R$1.550, 00
(c) R$1.600, 00
(d) R$1.650, 00
(e) R$1.680, 00
.
Professor Podô
[email protected]
2