IX TEORIA DE GRAFOS

IX TEORIA DE GRAFOS
9.1 Seja G o grafo cuja matriz de adjacência é:
1 2 3 4 5 6 7 8 9
1
1 1
2
1 1
3
1
4 1
1 1 1
5 1 1 1 1 1 1
6 1 1 1
7
1
8
1 1
9
1
Determinar o grau de cada vértice.
Fazer uma representação de G.
Verificar se há um caminho entre 1 e 9.
Escrever as componentes conexas de G.
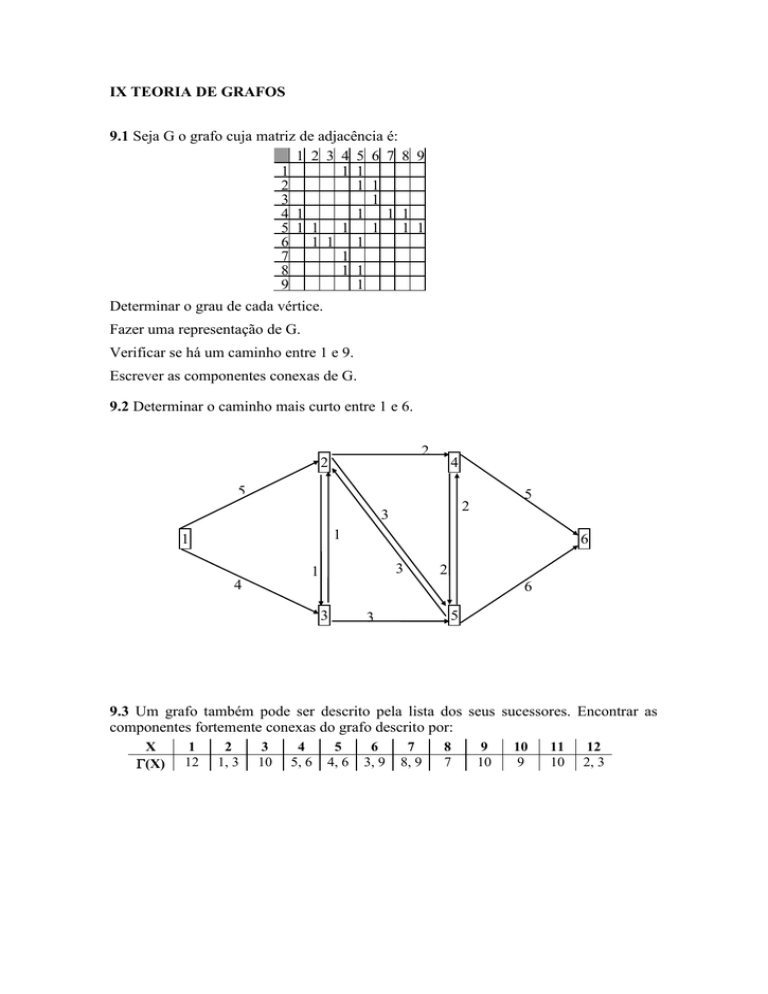
9.2 Determinar o caminho mais curto entre 1 e 6.
2
2
4
5
5
2
3
1
1
6
3
1
2
4
6
3
5
3
9.3 Um grafo também pode ser descrito pela lista dos seus sucessores. Encontrar as
componentes fortemente conexas do grafo descrito por:
X
(X)
1
12
2
1, 3
3
10
4
5, 6
5
4, 6
6
3, 9
7
8, 9
8
7
9
10
10
9
11
10
12
2, 3
9.4 Seja G o grafo descrito por:
X
1
2
3
(X) 2,3,4 1,3,5 1,2,4
4
7
5
3,6,7
6

7
5,6
8
9,10
9
8,10
10
8,9
Representar matricialmente o grafo.
Determinar as componentes fortemente conexas de G.
Determinar as componentes conexas de G.
Representar graficamente o grafo.
Representar graficamente as relações entre as componentes fortemente conexas.
9.5 Dar exemplo de um grafo não orientado com quatro vértices de ordens 1,3,3,3. É
possível encontrar um grafo simples nas condições anteriores?
9.6 Encontre um caminho no grafo
1
5
2
3
4
que passe por todas as arestas sem repetição.
9.7 Um grafo tem dez vértices numerados de 1 a 10. Existe uma aresta entre i e j se i + j
é ímpar e corresponde-lhe o custo | i  j |.
Escrever a matriz de adjacência correspondente.
Será o grafo conexo? Justificar.
9.8 Verificar teoricamente se no seguinte grafo é possível construir um circuito
Euleriano contendo todas as arestas e, em caso afirmativo, construa-o.
1
7
6
2
8
5
3
4
9.9 Determinar as componentes fortemente conexas do grafo representado na seguinte
matriz de adjacências:
1 2 3 4 5 6
1
1 1 1
2
1
3
1
4 1 1 1 1 1
5 1 1 1 1
6
1
9.10 Seja G um grafo. G é o seu grafo complementar se e só se o conjunto de vértices
de ambos for o mesmo e uma aresta existe em G se e só se não existe em G . Atendendo
a esta definição preencha a seguinte tabela:
K9
Nº de vértices
Nº de arestas
Perímetro
Soma dos graus
vértices
K9,9
K4,5
K 9,9
K 4,5
dos
9.11 Um grafo completo tripartido Kr,s,t consiste em três conjuntos de vértices com r, s e
t elementos respectivamente, tal que dois vértices estão ligados por uma aresta se e só se
estão em conjuntos diferentes.
a) Representar graficamente K2,2,2 e K2,2,3.
b) Quantos vértices e arestas tem Kr,s,t ? Justificar.
c) Quantas componentes conexas tem Kr , s,t ? Justificar. Como se pode classificar cada
componente conexa ?
d) Quantas arestas tem Kr , s,t ? Justificar.
9.12 É possível ter um grafo não orientado com oito vértices de graus: 2, 2, 3, 4, 5, 5, 6,
e 8 ? Justificar.
9.13 Sejam A1 = {1,2,3,4,5}, A2 = {2,4,6,8}, A3 = {3,5,12} e A4 ={5,8,10}. Desenhar o
grafo de vértices A1 ,A2 ,A3 ,A4 , tal que existe uma aresta entre dois vértices se e só se a
intersecção é não vazia. Construir a matriz de adjacência do grafo.
9.14 O seguinte diagrama é a planta de uma casa:
A
B
C
D
E
F
Existe alguma forma de percorrer a casa (iniciando o trajecto dentro ou fora da casa)
passando por cada porta uma e uma só vez ?
9.15 Um grafo simples diz-se bipartido se os seus vértices podem ser divididos em dois
conjuntos A e B, de modo que cada aresta do grafo liga um vértice de A com um vértice
de B. Determinar quais dos seguintes grafos são bipartidos:
a)
b)
v2
v1
v1
v2
v3
v1
v4
v5
9.16 Considere-se o seguinte mapa:
v4
v6
v3
c)
v3
v2
v1
v5
v2
d)
v3
v4
v6
v7
v5
B
A
Cada aresta representa uma avenida e cada vértice representa uma esquina entre
avenidas. Pretende-se entregar o correio nesta área iniciando a entrega no ponto A e
terminando no ponto B, passando em cada avenida exactamente uma vez.
9.17 Considere o seguinte grafo não orientado valorado:
A B C D
2
A
1
B 2
1
10
C
10
D
8 4 1
E
F 6 5 2
E F
6
8 5
4 2
1
1
1
Quantos caminhos de comprimento ( nº de arestas ) 3 existem entre os vértices A e D ?
Quais são ? Destes qual é o menos pesado e qual é o mais pesado ?
Utilizando o algoritmo de Dijkstra determine o caminho mais barato entre os vértices A
e D.
9.18 Determine a árvore geradora mínima do grafo:
A B C D E F
2
6
A
1
8 5
B
10 4 2
C 1
3
6
D
5 2
1
E 3
3
4
F
9.19 Verifique se são tripartidos os seguintes grafos:

1
4 
5


8

2

6
 7

3
A
B
C
D
E
A B C D E
1 1 1
1
1
1
1
1
1
1
F
1 1 1
F
1
1
1
1
9.20 Seja G um grafo simples não orientado com n vértices e k componentes conexas.
Mostre que se cada componente conexa de G é uma árvore, então G tem exactamente n
 k arestas.
9.21 Mostrar que num grafo simples existem, pelo menos, dois vértices com o mesmo
grau.
9.22 Redesenhar os seguintes grafos planares de forma a que não haja cruzamento de
arestas e identificar as faces dos grafos.
 1
 3
2 
 5
4 
a

b

d 
a

b

c


d

e

f
1

c

2 
 e
 3

4

f

5
9.23 Verificar que qualquer grafo simples com 4 vértices é planar.
9.24 Derivar uma fórmula análoga à fórmula de Euler ( f  e + v = 2 ) para grafos
planares não conexos.
9.25 Verificar que não são planares os seguintes grafos:

a)





















