Trigonometria - Sistemas PIBID

PROGRAMA INSTITUCIONAL DE BOLSA DE INICIÇÃO Á DOCENCIA
PROJETO MATEMÁTICA 1
TRIGONOMETRIA
Curitiba
2014
TÓPICOS DE GEOMETRIA PLANA
Ângulos
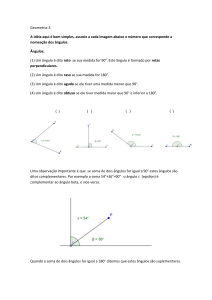
classificação:
Med(AôB) = 90°
Ângulo agudo:
Med(AôB) < 90°
Ângulo
reto:
mede
90°.
a
sua
medida
é
MENOR
que
a
do
ângulo
reto.
Ângulo obtuso: a
Med(<AOB) > 90°
sua
medida
é
MAIOR
que
a
do
ângulo
reto.
Ângulos complementares: Dois ângulos são complementares quando as suas medidas
somam 90°.
Ângulos suplementares: Dois ângulos são suplementares quando suas medidas somam
180°.
TRIÂNGULOS
Indicação: ∆ABC;
Lados: AB, BC e AC (ou a, b e c);
Vértices: A,B,C.
CLASSIFICAÇÃO DE TRIÂNGULOS QUANTO AOS LADOS
Triângulo Equilátero: os três lados são congruentes (iguais) e os três ângulos internos
são congruentes.
Triângulo Isósceles: dois lados são congruentes e dois ângulos da base são congruentes.
Triângulo Escaleno: possui uma medida diferente para cada lado e para cada ângulo.
CLASSIFICAÇÃO DE TRIÂNGULOS QUANTO AOS ÂNGULOS
Triângulo Acutângulo: todos os ângulos internos são agudos. <a, <b e <c são agudos →
med(<a) < 90º, med(<b) < 90º e med(<c) < 90º.
Triângulo Obtusângulo: possui umum ângulo interno obtuso. med(<a) > 90º ou
med(<b) > 90º ou med(<c) > 90º.
Triângulo Retângulo: possui um ângulo reto. med(<a) = 90º ou med(<b) = 90º ou
med(<c) = 90º.
→ A soma dos ângulos internos de um triângulo qualquer é 180º.
med(<a) + med(<b) + med(<c) = 180º.
RELAÇÕES MÉTRICAS NO TRIÂNGULO RETÂNGULO
Ângulos: Um triângulo retângulo possui um ângulo reto (90°) e dois ângulos agudos
(menores que 90°) complementares.
Obs: a soma dos ângulos internos de um triângulo é igual 180°.
Lados: Formado por três lados, uma hipotenusa (lado maior) e outros dois lados que são
os catetos.
Altura: A altura de um triângulo retângulo é um segmento que tem uma extremidade
num vértice e a outra extremidade no lado oposto ao vértice, sendo que este segmento é
perpendicular ao lado oposto a esse vértice. Existe três alturas no triângulo retângulo,
sendo duas delas os catetos a outra altura é obtida tomando a base como a hipotenusa.
Como mostra a figura:
Ainda em relação a altura do triângulo retângulo, temos:
- o segmento AD, chamado de h que representa a altura relativa a hipotenusa CB,
indicada por a.
- o segmento BD, chamado de m, representa o lado oposto ao cateto c sobre a
hipotenusa CB, indicada por a.
- o segmento DC, chamado de n, representa o lado oposto ao cateto b sobre a
hipotenusa CB, indicada por a.
Funções Trigonométricas Básicas:
Exemplo:
- para encontrar sen α de um triângulo retângulo temos que fazer b (cateto oposto ao
ângulo alfa (α)) sobre h (hipotenusa desse ângulo).
- para encontrar cos α, faremos a (cateto adjacente ao ângulo α) sobre h (hipotenusa
desse ângulo).
- para encontrar tg α, basta calcular b (cateto oposto ao ângulo α) sobre a (cateto
adjacenteà esse ângulo). Como mostra a figura acima.
Ângulos Notáveis:
DEMONSTRAÇÃO DE RELAÇÕES TRIGONOMÉTRICAS DO ÂNGULO DE
450
O objetivo desta sequência é a construção das relações trigonométricas do ângulo de
450. Para tanto, primeiramente vamos considerar o seguinte quadrado de lado :
Observe que a diagonal divide o quadrado ao meio em dois triângulos isósceles
de lado e ângulos da base de 450.
Problema 1: Utilizando o teorema de Pitágoras encontre o valor da diagonal AC em
função do lado :
Problema
2:
A
relação
seno
no
triângulo
retângulo
é
definida
por
0
. Considerando o triângulo abaixo encontre sen 45 . Não esqueça
de indicar o valor da diagonal AC encontrado no problema 1:
Problema
3:
A
relação
cosseno
no
triângulo
retângulo
é
definida
. Considerando o triângulo abaixo encontre cos 450:
por
Problema 5: A relação
tangente
no triângulo retângulo é
definida
por
0
. Considerando o triângulo abaixo encontre tg 45 :
TEOREMA DE PITÁGORAS
O teorema de Pitágoras se aplica ao triângulo retângulo e é representado por h2 = a2 +
b2, significa dizer que, a hipotenusa ao quadrado é igual a soma dos catetos ao
quadrado.
RELAÇÕES TRIGONOMÉTRICAS: TRIÂNGULOS QUAISQUER
Já fizemos o estudo da trigonometria no triangulo retângulo. Entretanto este é umcaso
particular de triangulo . Nesta parte da Trigonometria, abordaremos o estudo de todos os
triângulos, quaisquer que eles sejam. Este estudo se dará através de duas leis: Lei do
Senos e Lei dos Cossenos.
LEI DOS SENOS
“Em qualquer triangulo as medidas dos lados são proporcionais aos valores dos senos
dos ângulos opostos a estes lados e a constante de proporcionalidade é o dobro do raio
da circunferência circunscrita ao triangulo.”
LEI DOS COSSENOS
“Em um triangulo qualquer o quadrado de um dos lados é igual à soma dos quadrados
dos outros dois lados menos o dobro do produto desses lados pelo cosseno do ângulo
que está entre eles.”
Utilizamos a Lei dos Cossenos quando temos três lados e um ângulo. Casocontrario, ou
seja, se tivermos quantidades iguais de lados e ângulos ou quando possuímos um lado,
um ângulo e um raio da circunferência circunscrita ao triangulo (inclui-se, nestes casos ,
a variável) aplicamos a Lei dos Senos.
FUNÇÕES TRIGONOMÉTRICAS
Em meados do século XVI, François Viète, advogado francês dedicado à pesquisa
matemática, destacou-se por recorrer sistematicamente ao círculo trigonométrico e
aplicar a Trigonometria na resolução de problemas algébricos, contribuindo, assim, com
o desenvolvimento da Matemática. Todo esse processo culmina com a introdução do
conceito de seno, cosseno e tangente como números reais, feita por Leonhard Euler (
século XVIII), quando ele passa a considerar a circunferência trigonométrica de raio
unitário.
A representação das relações trigonométricas na circunferência de raio unitário levou os
matemáticos a estudarem seu comportamento, esboçando-as graficamente.
FUNÇÃO SENO
Associando cada numero real x a um arco da circunferência trigonométrica, com origem
no ponto A (1,0) e extremidade em um ponto P tal que m(AP) = x rad, dizemos que
seno do arco x é a ordenada OP’, do ponto P
sen x = OP’
Chamamos de função seno a função f:R R que, a cada numero real x, associa o seno
desse numero:
f:R R, f(x) = sen x
O domínio dessa função é R e a imagem é – [-1,1] visto que, na circunferência
trigonométrica, o raio é unitário e, pela definição de seno, -1 ≤ senx ≤ 1, ou seja|
D (sen x) = R
e
Im(sen x) = [-1,1]
SINAL DA FUNÇÃO
Como sen x é a ordenada do ponto-extremidade do arco:
f(x) = sen x é positiva no 1º e 2º quadrantes
(ordenada positiva)
f(x) = sen x é negativa no 3º e 4º quadrantes
(ordenada negativa)
FUNÇÃO COSSENO
Associando cada numero real x a um arco da circunferência trigonométrica, com origem
no ponto A (1,0) e extremidade em um ponto P tal que m(AP) = x rad, dizemos que
cosseno do arco x é a abcissa O
do ponto P
cos x = OP’
Chamamos de função cosseno a função f:R R que, a cada numero real x, associa o
cosseno desse numero:
f:R R, f(x) = cos x
O domínio dessa função é R e a imagem é [-1,1] visto que, na circunferência
trigonométrica, o raio é unitário e, pela definição de seno, -1 ≤ cos x ≤ 1, ou seja
D (cos x) = R e Im(cos x) = [-1,1]
SINAL DA FUNÇÃO
Como cos x é a abscissa do ponto-extremidade do arco:
f(x) = cos x é positiva no 1º e 4º quadrantes
(abscissa positiva)
f(x) = cos x é negativa no 2º e 4º quadrantes
(abscissa negativa)
EXERCÍCIOS
1- Um avião levanta voo em um ângulo de 30° em relação à pista. Qual será a altura
do avião quando estiver percorrendo 4 000 m em linha reta?
2- Dado um triângulo equilátero de lado 20 cm, calcule a medida da altura desse
triângulo.
3- Um avião levanta voo sob um ângulo de 30º. Depois de percorrer 8 km, o avião se
encontra a uma altura de:
a) 2 km b) 3 km c) 4 km d) 5 km
4- (UF – PI) Um avião decola, percorrendo uma trajetória retilínea, formando com o
solo, um ângulo de 30º (suponha que a região sobrevoada pelo avião seja plana).
Depois de percorrer 1 000 metros, qual a altura atingida pelo avião?
a) 300m b) 400m c) 500m d) 600m e) 700m
5- Ao decolar, um avião sobe formando um ângulo de 30º com a pista (horizontal). Na
direção do percurso existe uma torre de transmissão de energia elétrica situada a
3km do aeroporto, e com altura igual a 150m. Verifique se, mantendo o trajeto, o
avião pode colidir com a torre.
5-Determine o valor de sen α, cos α e tg α no triangulo retângulo a seguir:
6-Sabendo que tg α = ¾, calcule o valor da expressão sen α+ cos α.
7-Calcule o cosseno de α do triangulo abaixo:
8- (UFPR-LITORAL) Um triângulo retângulo possui um cateto medindo 6cm e área de
9 cm².Quanto mede a hipotenusa desse triângulo?(área do triângulo = base x altura/2 )
9- Observe a figura a seguir e determine a altura “h” do edifício, sabendo que AB mede
25m e sen ϴ= 0,8 .
10- Uma escada está apoiada em um muro de 2 m de altura, formando um ângulo de
45º. Forma-se, portanto, um triângulo retângulo isósceles. Qual é o comprimento da
escada?
11- Ao empinar uma pipa, João percebeu que estava a uma distância de 6m do poste
onde a pipa engalhou. Renata notou que o ângulo formado entre a linha da pipa e a rua
era de 60º. Calcule a altura do poste.
12- (Cefet – PR) A rua Tenório Quadros e a avenida Teófilo Silva, ambas
retilíneas, cruzam-se conforme um ângulo de 30º. O posto de gasolina Estrela do Sul
encontra-se na Avenida Teófilo Silva a 4000m do citado cruzamento. Portanto,
determine em quilômetros, a distância entre o posto de gasolina Estrela do Sul e a rua
Tenório Quadros?
13- No triângulo retângulo da figura abaixo, determine as medidas de x e y indicadas
(Use: sen 65° = 0,91; cos 65° = 0,42 ; tg 65° = 2,14)