Módulo 1 - Flavio Colmati

Universidade Federal de Goiás
Instituto de Química
Graduação
Disciplina INQ0021 – Eletroquímica e Corrosão
Módulo 1 –
células galvânicas e
propriedade dos eletrólitos
Prof. Flavio Colmati
Prof. Dr. Flavio Colmati IQ-UFG
Células galvânicas
São dispositivos que convertem energia química em
energia elétrica.
É um dispositivo (sistema) capaz de realizar trabalho
elétrico nas vizinhanças, a partir de uma reação
química (da reação da pilha)
2
Células galvânicas
Um sistema eletroquímico é constituído por (no mínimo)
• 2 Eletrodos (condutor de elétrons)
• 1 Eletrólito (condutor de íons)
Eletrodo
Eletrodo
Eletrólito
3
1
Células galvânicas
Ânodo – Oxidação
/
Cátodo – redução
ne-
e-
e-
R
O
O
R
R O + ne-
O + ne- R
4
Células galvânicas
A reação química que ocorre na célula galvânica deve ser uma
reação espontânea
eO2(g)
H2(g)
H2SO4
Pt
H+
H2 2 H+ + 2e-
Pt
½ O2 + 2 H+ + 2e- H2O
H2 + O2 H2O
Em alguns casos, os eletrólitos tem que ser mergulhados em eletrólitos
diferentes:
5
Alessandro Volta (1796) descobriu a pilha voltaica composta
por dois metais e papel embebido em eletrólito (salmoura).
https://global.britannica.com/biography/Alessandro-Volta
http://brasilescola.uol.com.br/quimica/historia-das-pilhas.htm
6
2
Pilha de Daniell
Os eletrodos são colocados em compartimentos separados
John Frederic
Daniell, 1836
CuSO4
ZnSO4
Zn2+ + SO4-2
Cu2+ + SO4-2
NH4NO3 ou KCl
Quando as placas são conectadas observa-se que a reação química
acontece, a placa de zinco começa a se dissolver e cobre metálico é
depositado sobre a placa de cobre.
7
Células galvânicas
par redox é Zn/Zn2+
Zn Zn2+ + 2e-
par redox é Cu/Cu2+
Pilha de Daniell:
Reação de oxidação do zinco
Reação global: Zn +
2e- + Cu2+(aq) Cu
Reação de redução do cobre
Cu2+(aq)
Zn2+ + Cu
as reações de oxidação-redução ocorrem separadas em duas semi-reações:
8
Analisando o que acontece em cada béquer
CuSO4
ZnSO4
Zn2+ + SO4-2
Observa-se que há um fluxo de
elétrons proveniente da placa de
zinco, e íons zinco são
produzidos a medida que a placa
se dissolve, assim, pode-se
escrever a seguinte reação:
Zn Zn2+ + 2e-
Cu2+ + SO4-2
NH4NO3
ou KCl
Observa-se que o fluxo de
elétrons vai para a placa de
cobre, e os íons cobre da solução
são depositados sobre a placa,
pode-se escrever a seguinte
reação :
2e- + Cu2+(aq) Cu
A solução de Zn2+ fica mais concentrada e a de Cu2+ fica mais diluída
9
3
Função da ponte salina
Zn Zn2+ + 2e-
2e- + Cu2+(aq) Cu
Excesso de Zn2+
Excesso de SO42-
10
Células galvânicas
Célula galvânica é um dispositivo que utiliza reações de óxido-redução
para converter energia química em energia elétrica.
A reação química sempre será uma reação espontânea.
Uma reação espontânea....
Critério de espontaneidade:
Aumento da entropia total (dStot ≥ 0)
dS tot = dS sis + dS vis
2ª Lei da termodinâmica:
Em um sistema isolado a entropia do sistema não pode
diminuir quando ocorrer uma transformação
espontânea
11
Reações eletroquímicas ocorrem a pressão constante, então:
1ª Lei da termodinâmica
(dU função de estado):
dU = dq + dw
dU = dqrev + dwrev
Chega-se à
P = constante
dqP = dH
Então: dq + dw = dqrev + dwrev
dS ≥ Nas reações eletroquímicas:
TdS ≥ dH
dH - TdS ≤ 0
define
H – TS = G energia de Gibbs
Desigualdade de Clausius
TdS ≥ dq
dG = VdP + SdT + we
A temperatura e pressão constante:
dG = we rev
12
4
•
•
•
•
Assim, quando:
ΔG > 0 – Processo ocorre no sentido oposto ao indicado
ΔG < 0 – Processo ocorre espontaneamente
ΔG = 0 – Processo está em equilíbrio dinâmico
Para reações químicas
∆
exemplo
Δ
½ H2(g) + ½ Cl2(g) H+(aq) +Cl-(aq)
Δ
∆rGo = -131,23 kJ mol-1
O critério dGT,P ≤ 0 diz que a temperatura e a pressão constante, as reações
químicas são espontâneas no sentido de diminuição da energia de Gibbs
13
Células galvânicas
Reações nas células galvânicas devem ser espontâneas:
trabalho elétrico = energia de Gibbs
Reação global: Zn + Cu2+(aq) Zn2+ + Cu
Uma pilha, onde a reação global não atingiu o equilíbrio, pode realizar
trabalho elétrico a medida que a reação avança
∆ Onde ξ é o avanço da reação
14
Células galvânicas
∆ Zn + Cu2+(aq) Zn2+ + Cu
Onde ξ é o avanço da reação
Temos:
∆ = ! "
# $% ln (
) ) # $% ln ()
* * # $% ln (*
∆ ∆
# $% ln (* / ()
15
5
∆ ∆
Onde (* / ()
# $% ln (* / ()
= Q quociente da reação
Q = π aj νj onde a é a atividade, v é o coeficiente estequiométrico da espécie j
Da equação:
∆ ∆
# $% ln -
no equilíbrio: ∆ = 0
Q=k
Assim a equação fica:
∆
$% ln ,
16
O trabalho máximo que o sistema pode fazer é:
w el, máx = ∆rG
Para obter dados termodinâmicos devemos garantir
que a reação da pilha seja reversível
W rev trabalho máximo
Além disso,
∆ relacionada com a composição
∆ = ! "
17
∆ relacionada com a composição
∆ Quando há um avanço infinitesimal na reação, a variação de
dG é:
dG = ∆ .
O trabalho elétrico que pode ser
realizado é:
w el, max = ∆ .
Se a reação avança ., 0. elétrons são transferidos:
a carga total transferida é dada por um equivalente de elétrons -e N (=F)
Resultando em uma transferência de carga de: -eN ndξ ; =
-Fndξ
O trabalho elétrico é dado por : dw = ΦdQ
Onde Φ é o potencial elétrico (V) e dQ é a variação de carga elétrica (C)
w e, max = -nFE dξ
18
6
Temos:
w e, max = -nFE dξ
w el, max = ∆ -nFE dξ = ∆ .
-nFE dξ = ∆ .
-nFE = ∆
Logo
ou
∆ −nFE
Onde F é a constante de Faraday, v é o coeficiente estequiométrico dos
elétrons nas meias reações.
Essa equação correlaciona medidas elétricas com medidas termodinâmicas
19
∆ relacionada com a composição
∆ ∆
# $% ln Q
Dividindo a equação por -nF
∆/01 ∆
Como
/34
E=
# $%/34 ln Q
∆ !01
Podemos definir que no estado padrão, ∆
-vFEo = ∆
5
E E
67 ln Q
,
E = Eo e assim:
2
Equação de Nernst
Walther Hermann Nernst
1864-1941
20
No equilíbrio Q = K e que ∆ = 0
∆ = -vFE = 0
Então E = 0 e a célula galvânica não produz trabalho
Então :
5
E E
67 ln Q
5
0 E
67 ln K
5
E
# 67 ln K
21
7
Relações entre Eo, ∆Go e K:
∆ 2 −nFEo
E
5
67
∆
ln K
$% ln ,
22
exemplo
Dada a reação:
Zn + Cu2+(aq) Zn2+ + Cu
Qual é a constante de equilíbrio?
Sabe-se que o potencial padrão dessa célula galvânica é 1,1 V e que
são transferidos 2 elétrons, assim:
E
#
5
67
ln K
1,1 V #
5
67
ln K
A 25 oC, RT/F é igual a 25,693 mV ou 0,02593 V
23
5
1,1 V # 67 ln K
ln k = 1,1 V
1,1 V 8
0,0259630
0,02593 V
6
ln K
v=2
V
ln k = 85,63
Assim chegamos que a constante de equilíbrio da reação é :
k = 1,5x1037
Lembrando que K = [prod]/[reag]
Essa formação de produtos é muito favorecida.
24
8
Potencial Elétrico
O Potencial elétrico (Φ ) de um ponto P é o trabalho
para se levar uma carga unitária positiva do infinito
até o ponto P.
= >?
>-
Φ é o potencial elétrico no ponto e w é o trabalho necessário para levar a
carga Q do infinito até o ponto P
25
Se φ1 e φ2 forem os potencias elétricos de dois
pontos no espaço,
w1 e w2 o trabalho para levar a carga Q a P1 e P2
W12 é o trabalho gasto para levar a carga Q do ponto 1 ao ponto 2
w2 = w1 + w12
w2 = w1 + w12
26
w12 = w2-w1
Como φ=dw/dQ d w= φ dQ
dW12 = φ2dQ – φ1dQ
dW12 = (φ2- φ1) dQ
dW12/dQ = φ2- φ1
Φ1 e Φ2 são os potencias
elétricos de dois pontos no espaço
A diferença entre os potenciais elétricos (φ2- φ1) é o trabalho
necessário para conduzir uma carga unitária positiva do
ponto 1 até o ponto 2.
27
9
dW 12 = (φ2- φ1) dQ
E = Φ2- Φ1
E = Diferença de Potencial
dw12 = dw elétrico
dWel = E dQ
dG = dw elétrico
Então: E dQ = dwele
(Φ2- Φ1)dQ = dG
dG = E dQ
28
A tendência de escape de partícula carregadas de uma fase,
depende do potencial elétrico da fase
n e-
Dois eletrodos – mesmo metal
Φ1 e φ2 Os potenciais elétricos
de M1 e M2
n moles de elétrons são
transferidos de M1 para M2
M1
M2
dwel = (φ2 - φ1) dQ
dG = (φ2 - φ1) dQ
29
O potencial químico do elétron (µe) quando são
transferidos dn moles de elétrons é:
dG = µe2 dn - µe1 dn
(φ2- φ1)dQ = dG
e
dQ = -Fdn então
(φ2- φ1)dQ = µe2 dn - µe1 dn
(φ2- φ1) -F dn = (µe2 - µe1 )dn
O potencial químico (µe) do elétron,
-(φ2- φ1) F = (µe2 - µe1 )
quando Φ = zero é: µe = µe2 + Fφ2
µe1 = µe2 + Fφ2-Fφ1
µe2 = µe + Fφ1
Potencial
eletroquímico
Potencial
químico
Contribuição
elétrica
Generalizando para qualquer espécie carregada situada em uma fase
µe’ = µe + ziFφ1
10
Potencial químico das espécies carregadas
µe’ = µe + ziFφ1
Íons em solução: φ = 0 ; µe’ = µe
Eletrodos (metais) µe = 0 µe’ = F φ
31
Potencial da pilha (E)
Uma pilha galvânica é uma combinação entre dois eletrodos, ambos
contribuindo para a reação global da pilha.
Não é possível medir a contribuição de um eletrodo isolado,
entretanto, pode-se atribuir um padrão.
Eletrodo de referência -
• O eletrodo que tomamos como referência é o eletrodo padrão de
hidrogênio (EPH).
• Pt|H2(g)|H+(aq) Eo = 0
• Em todas as temperaturas
32
O eletrodo padrão de hidrogênio
Uma chapa de platina em contato com H2(g)
em solução ácida (H2SO4)
1
@ A (B # C ! DE ⇄ @8 I
2
E H2/H+ = 0
33
11
potencial-padrão, Eo.
Usando a pilha: Pt(s)|H2(g)|HCl(aq)|AgCl(s)|Ag(s)
½ H2(g) + AgCl HCl(aq) + Ag(s)
A equação de Nernst é:
J J J J #
$% (@ . (MN
ln
34
(1/2@2
J J #
$% (@ . (MN
ln
34
$%
ln K (
34
Considerando aH2 = 1 (a = atividade)
a atividade é : a = γ b (γ = coeficiente de atividade; b = molalidade)
e usando a lei de Debye-Huckel para eletrólito 1:1
34
potencial-padrão, Eo.
J #
2$%
ln O J # MOP/8
4
Mede-se E vs b em uma faixa de b (lado esquerdo da eq)
Grafica b1/2 vs E e extrapola a reta para b = 0.
O valor da intercepção em b1/2 = 0 é Eo
Alguns potenciais padrão, a 298 K são registrados
35
36
12
Potencial de célula (E)
força eletromotriz
A diferença de potencial entre os eletrodos de uma célula
galvânica é chamada de:
voltagem da célula, ou
potencial da célula, ou
Força eletromotriz.
2e- + Cu2+(aq) Cu Eo
Zn Zn2+ + 2e- Eo
Reação global: Zn + Cu2+(aq) Zn2+ + Cu
Epilha
37
• A voltagem da célula é calculado a partir dos potenciais
dos eletrodos:
• E célula = E direita – E esquerda (ou)
• E célula = E redução – E oxidação
Os potenciais Ered e E oxi são potencias de cada meia-célula obtido pela
equação de Nernst.
38
∆ Q −nFE
O potencial (E) varia com a energia de Gibbs
O potencial (E) depende da corrente extraída
pelo circuito elétrico
limW WXY
T→V
O potencial (E) é uma propriedade intensiva
39
13
Potencial de célula (E)
força eletromotriz
2e- + Cu2+(aq) Cu Eo = 340
Zn Zn2+ + 2e- Eo = 760
Zn Zn2+ + 2e- Eo = 760
2e- + Cu2+(aq) Cu Eo = 340
Reação global:
Zn + Cu2+(aq) Zn2+ + Cu
Epilha = 1100 mV
40
notação
• Para simplificar
• Na notação das pilhas eletroquímicas, pode-se
representar:
• Interfaces | (uma barra vertical)
• Junção líquida ⁞ (pontos na vertical)
• Interfaces (sem Ejl) || (duas barras vertical)
41
Células galvânicas
Notação:
ou, segundo IUPAC
Zn| Zn2+(aq)||Cu2+(aq)|Cu
Fronteira de fase
Ponte salina
(interface)
Semi-reação do lado esquerdo = oxidação
Semi-reação do lado direito = redução
42
14
Zn | Zn2+ ⁞ Cu2+ | Cu
43
Pt(s) | H2(g) | HCl | Ag+ | Ag(s)
44
exemplo
Célula de Zn/Cu
E célula = Ered – E oxi
Célula Zn| Zn2+(aq)||Cu2+(aq)|Cu
E cel = +0,34 – (-0,76) = 1,1V
Como ΔG = - nFE
ΔG = - 2*96500*1.1 = - 212 000 VC mol-1
V*C = Joule
ΔG = - 2*96500*1.1 = - 212 kJ mol-1
O que mostra que a reação é espontânea na direção que foi escrita.
45
15
Hg|Hg2Cl2|Cl-(aq)||Zn2+(aq)|Zn
A reação é:
2Hg + 2Cl- +Zn2+ Hg2Cl2 + Zn
As meias reações:
Zn2+ + 2e- Zn
Hg2Cl2 + 2e- 2Hg + 2Cl• Ecélula = E red – E oxi
• -0,76 + (+0,27) = -1,03V
ΔG = -nFE
ΔG = -2 96500 -1,03 = +198 103 CV mol-1
1 C.V = J
ΔG = +198 kJ mol-1
ΔG > 0Reação espontânea é oposta a
que foi proposta.
46
Pilha de concentração
Em uma pilha de concentração no eletrólito, os compartimentos
eletródicos são idênticos, exceto a concentração do eletrólito
Cu
Cu
Cu2+
Cu2+
Uma célula galvânica desse tipo pode funcionar?
Qual é a direção que os elétrons fluem no circuito externo?
Equação de Nernst:
E = Eo – RT/nF ln Q
E = Eo – RT/nF ln [diluído]/[concentrado]
47
Efeito da concentração
O potencial do eletrodo depende da
concentração dos íons
E = Eo – RT/nF ln Q
E = Eo – RT/nF ln [diluído]/[concentrado]
E = Eo – 0,0257/2 ln [Cu 2+ diluído]/[Cu2+ concentrado]
E = Eo – 0,0257/2 ln [0,01]/[1]
Eo = 0
O mesmo eletrodo e os mesmos íons estão envolvidos
E = 0 – 0,0257/2 ln [0,01]/[1]
E = 0,059V
48
16
Eletrólitos
Eletrólitos ou solução Eletrolítica
Solução é uma mistura homogênea de duas ou mais substâncias
O solvente é a substância presente em maior quantidade
O soluto é a substância presente em menor quantidade
Eletrólitos
Soluto
solúveis em
água
Duas
categorias
Não
Eletrólitos
49
É uma substância que, quando dissolvida
em água produz uma solução capaz de
conduzir eletricidade
Eletrólito
Não Eletrólito
Não conduz eletricidade quando
dissolvido em água
50
exemplo
Ânodo – Oxidação
redução
/
Cátodo –
ne-
e-
R O + ne-
e-
R
O
O
R
eletrólitos
O + ne- R
Não eletrólitos
51
17
Efeito solubilidade
Com o desenvolvimento:
da teoria atômica e
da estrutura cristalina
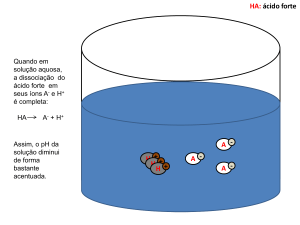
eletrólitos fortes,
completamente ionizadas
mesmo no estado
sólido, como o NaCl.
O cristal de NaCl é constituído por íons sódio e íons cloreto
unidos por força eletrostática.
Quando adicionados em água, os íons são afastados e a
dissociação é completa.
http://mundoeducacao.bol.uol.com.br/quimica/cloreto-sodio.htm
52
Como o NaCl é um composto estável no qual íons Na+ e Cl- estão ligados
por forças eletrostáticas na rede cristalina.
A dissolução do NaCl em água
1) Como os íons interagem com as moléculas de água?
2) Como os íons interagem um com o outro?
53
1) Como os íons interagem com as moléculas de água?
A água é um bom solvente para compostos iônicos porque é uma
molécula polar e pode estabilizar os íons por interação íon-dipolo, que resulta em
uma hidratação.
http://www.quimicasuprema.com/2013/10/forcasintermoleculares.html
http://mundoeducacao.bol.uol.com.br/quimica/forcas-ouligacoes-dipolo-dipolo.htm
54
18
1) Como os íons interagem com as moléculas de água?
íons pequenos tem a carga mais concentrada maior
interação eletrostática com as moléculas de água.
O número de hidratação:
é diretamente proporcional à carga
inversamente proporcional ao tamanho do íon.
http://www.profpc.com.br/%C3%81gua/%C3%81gua.htm
55
A interação íon-dipolo entre íons dissolvidos e moléculas de
água pode afetar várias propriedades da água no interior da
solução.
Íons pequenos ou multicarregados íons estruturantes.
o campo elétrico polariza moléculas de água
Fonte: https://www.wou.edu/las/physci/ch412/hydspher.gif
56
íons grandes e monovalentes íons desestruturantes, carga superficial difusa e portanto o campo elétrico fraco polariza primeira camada de hidratação.
http://www.profpc.com.br/%C3%81gua/%C3%81gua.htm
57
19
2) Como os íons interagem um com o outro ?
A carga elétrica qA produz campo elétrico E
De acordo com Coulomb, A energia potencial entre as cargas é
Z B1B2
4Πε
εo que é a permissividade do vácuo
A força eletrostática entre as cargas:
4 B1B2
4^_
2
58
Moléculas de água se alinham:
Arranjo reduz a carga efetiva dos íons
http://www.78stepshealth.us/human-physiology/ionicbonds.html
59
Quando o íon está em qualquer outro meio, diferente do
vácuo, a equação se torna:
4 B1B2
4^__
2
Permissividade de líquidos puros a 298K
Líquido
permissividade
H2O
78,54
C6H6
4,6
Permissividade é adimensional é diminui com o aumento da temperatura
a elevada permissividade de água é o que reduz a força atrativa
entre os íons (Na+ e Cl-) e permite que se separem em solução.
60
20
Ao se adicionar um eletrólito em água ele se dissocia a forma íons em solução
)* ⇌ B+ + A-
Cátions e ânions se atraem em um sólido iônico, criando uma
energia de ligação.
Para que estes íons sejam separados:
uma certa quantidade de energia deve ser fornecida, sendo
suficiente para que quebrar a ligação ânion-cátion.
Esta energia é denominada energia de rede (U).
61
NaCl(s) Na+(g) + Cl- (g)
E é possível conhecer o valor da energia de rede (U)
A variação de entalpia dessa reação corresponde à
energia requerida para afastar os íons da rede cristalina a uma
distancia infinita.
Essa energia é a energia de rede (U)
podemos usar os parâmetros termodinâmicos de dissolução de
compostos iônicos em água, formando íons em solução.
62
Para obter o valor da energia de rede do NaCl,
podemos usar a lei de Hess:
Na+(g) + Cl-(g)
Entalpia de hidratação (∆H
NaCl(s)
hidr)
Na+(aq) + Cl-(aq)
A lei de Hess diz: ∆ hidr H = ∆ sol H - U
63
21
∆ sol H = 3,8 kJ mol-1
U NaCl = 787 kJ mol-1
∆ hidr H = ∆ sol H - U
∆ hidr H = 3,8 – 787
∆ hidr H = – 783,2 kJ mol-1
∆ hidr H << 0, hidratação dos íons Na+ e Cl- liberam
grande quantidade de energia na forma de calor (q)
∆H = qp
64
∆ hidr H = – 783,2 kJ mol-1
hidratação dos íons Na+ e Cl-
Para saber o valor de ∆hidrH de cada íons é necessário usar o dado de
entalpia de hidratação do íon hidrogênio, obtido por cálculos teóricos:
H+(g) H+(aq)
∆hidrH = - 1089 KJ mol-1
Partindo desse dado pode-se calcular ∆ hidr H de outro íons isoladamente.
Valores termodinâmicos de hidratação de íons gasosos a 298K
Íon
ΔhidrH / kJ mol-1
Na+
-405
K+
-314
Ag+
-468
Cu2+
-2092
F-
-506
Br-
-348
Cl-
-378
65
Entropia de hidratação ∆ hidr S.
solvatação/hidratação do íon ordenamento das moléculas de
água, ∆ hidr S negativo
Valores termodinâmicos para a hidratação de íons gasoso a 298K
Íon
ΔhidrS / J mol-1 K-1
Li+
-119
Na+
-89
Mg2+
-243
K+
-51
Cl-
-96
66
22
Entalpia (H) de formação de íons em solução
Dada a reação:
½ H2(g) + ½ Cl2 H+(aq) + Cl-(aq) ∆rHo = -167,2 Kj mol-1
Sabemos que a entalpia padrão de reação é obtida a partir das
entalpias padrões de formação:
∆H = Σ ν∆fHo
(prod)
- Σ ν∆fHo (reag)
não é possível medir a entalpia padro de formação de um íon individual;
definido arbitrariamente
∆Hf H+(aq) = 0
a partir desse valor, pode-se determinar os valores de ∆fH de outros íons
67
Entalpia padrão de reação medir experimentalmente :
½ H2(g) + ½ Cl2 H+(aq) + Cl-(aq) ∆rHo = -167,2 Kj mol-1
∆rHo = ∆fHo H+ (aq) + ∆fHo Cl- (aq) – ½ (0) - ½ (0)
Chegamos ao valor de
∆rHo = ∆fHo Cl- (aq)
∆Hof (Cl- aq) = -167,2 KJ mol-1
68
O mesmo procedimento pode ser realizado para a energia
de Gibbs e para a entropia, para isso é necessário definir
∆Gof (H+ aq) = So = 0
Dados termodinâmicos de íons aquosos a 298K
ΔfHo / KJ mol-1 ΔfGo / KJ mol-1 So / J mol-1 K-1
Íon
Li+
-278,5
-293,8
14,23
Na+
-239,7
-261-9
60,25
K+
-251,2
-282,3
102,5
Mg2+
-462,0
-456,0
-138,1
Zn2+
-152,4
-147,2
-112,1
OH-
-229,9
-157,3
10,54
Cl-
-167,2
-131,2
56,5
NO3-
-206,6
-110,5
146,4
69
23
Potencial químico
• a bc
bd
• Em geral, o potencial químico varia com a
composição
70
Potencial químico dos líquidos
Vapor
Equilíbrio
eí 6
Líquido
71
• 6 " ) # $%N3D"
∗
• eg "eg ) # $%N3D"
• Então
" ∗ ) # $%N3
• eg " ) # $%N3D"
∗
puro
mistura
i"
∗
i"
72
24
• " ∗ ) # $%N3
i"
∗
i"
• Lei de Raoult : j" • " ∗ ) # $%N3j"
i"
∗
i"
Soluções ideais - seguem a lei de Raoult
73
• Soluções reais
– Soluto obedece a lei de Henry
Quando xB 0
Lei de Henry: PB = kBxB
Alternativa, a lei de Henri pode ser escrita :
Lei de Henry: PB = kB’MB
M = molalidade da solução
74
A presença do soluto reduz o potencial químico do solvente
∗
" → " ∗ ) # $%N3j"
ln xA < 0
0< xA < 1
Para soluções reais
" ∗ ) # $%N3("
a é a atividade do solvente
75
25
A atividade do solvente em função da pressão
de vapor é:
(" D)
∗
D)
A atividade relacionada com a fração molar
(" k" j"
γA e o coeficiente de atividade
76
O potencial químico de uma solução não ideal
" ∗ ) # $%N3("
" ∗ ) # $%N3k" N3j"
γ é uma medida do desvio da idealidade
No limite x 1; γ 1
ax
77
Atividade do soluto
• Nas soluções não ideais diluídas
– O solvente obedece a lei de Raoult
– O soluto obedece a lei de Henry
eg ∗ * # $%N3j*
78
26
eg ∗ * # $%N3j*
Lei de Henry: PB = kBxB
eg * # $%N3(*
a B é a atividade do soluto
79
eg * # $%N3(*
( D*
l*
( k j
Os desvios da idealidade estão em γB
No limite aB xB ; γB 1
Quando xB 0
A atividade do soluto em função da
concentração molal :
eg ° * # $%N3n*
80
Atividade em soluções eletrolíticas
como escrever o potencial químico das soluções
eletrolíticas
Se o potencial químico de um
Cátion M+ é : µ+
Ânion X- é : µ-
O potencial químico da solução eletrolítica é:
µM+X- = µM+ + µX81
27
Cátions e ânions não podem ser estudados individualmente
Mas potencial químico podem ser escritos:
µM+ = µM+o + RT ln mM+
µX- = µX-o + RT ln mXµM+X-o = µM+ o+ µX-o
µM+X- = µM+X-o + RT ln M M+ MX-
82
generalizando
Eletrólitos tem a formula: Mν+Vν-
Mν+Vν- ⇌ ν+Mz- + ν-MzO potencial químico fica:
µ = ν +µ+ + ν –µµ+ = µ+o + RT ln mM+
µ- = µ-o + RT ln mX83
A molalidade do cátion e do ânion está relacionada com a
molalidade do eletrólito,
Assim:
µ = (ν +µ+o + ν –µ-o) + RT ln M+ ν+ M- ν-
Define-se – Molalidade iônica média (M±): M± = (M+ ν+ M- ν- )1/ ν
µ = (ν +µ+o + ν –µ-o) + RT ln (M+ ν+ M- ν- )1/ ν
Soluções eletrolíticas apresentam comportamento não ideal, então devese substituir molalidade por atividades
84
28
Define-se – atividade iônica média (a±):
a± = (a+ ν+ a- ν- )1/ ν
A atividade iônica média (a± )
e a molalidade iônica medias (M± ) estão relacionadas:
a± = γ ± M ±
e
γ ± = (γ + ν+ γ - ν- )1/ ν
85
• O potencial químico da solução eletrolítica
não ideal é:
µ = (ν +µ+o + ν –µ-o) + ν RT ln a±
µ = (ν +µ+o + ν –µ-o) + RT ln a± ν
a± ν = a
µ = (ν +µ+o + ν –µ-o) + RT ln a
86
A presença do soluto no solvente diminui o potencial químico do
solvente
∗
" → " ∗ ) # $%N3j"
ln xA < 0
0< xA < 1
Não há influencia do soluto no vapor
6
1
eí
1
eí 6
1
6 6
2
1
eí o eí
2
6
2
eí
2
87
29
• Propriedades coligativas:
– Abaixamento da pressão de vapor
– Elevação ebulioscópica
– Abaixamento crioscópico
– Pressão osmótica
Acontecem devido a redução do potencial químico do solvente
Acontecem em soluções ideais e em soluções reais
88
• Abaixamento da pressão de vapor
eí∗ 6
∗
eí o eí
89
• Elevação ebulioscópica T* T*+ΔT
• ΔT = Keb b
• Abaixamento crioscópico
• ΔT = Kf b
Keb = kf = RT*2 / ΔvapH
90
30
• Osmose – passagem do soluto
• Pressão osmótica ( π )- pressão aplicada para impedir
a osmose
π = [B] RT
Equação de van’t Hoff
91
Propriedades coligativas de soluções eletrolíticas
Propriedades coligativas são influenciadas pelo número de partículas presente na solução.
Exemplo:
0,01 M NaCl
0,01 M C6H12O6
NaCl Na+ + Cl-
O abaixamento do ponto de congelamento da água no NaCl é 2x o da C6H12O6
92
• Para eletrólitos não totalmente dissociados
Define-se o fator i ( fator de van’t Hoff)
i = no partículas na solução em equilíbrio
no de partículas antes da dissociação
93
31
Mν+Vν- ⇌ ν+Mz- + ν-MzN (1-α)
Nν-α
Nν+α
Nνα íons em solução
O fator de van’t Hoff (i) é:
p
q P!r Aqsr
q
t = 1- α + ν α
p 1
u 1
94
As equações utilizadas para determinar as
propriedades coligativas devem ser modificadas
Elevação ebulioscópica
∆T = Keb i b
Abaixamento crioscópico
∆T = Kf i b
osmose
π = i [B] RT
95
Eletrólitos
Teoria clássica da dissociação eletrolítica
partículas carregadas livre em soluções eletrolíticas (na forma de íons)
não foi aceita imediatamente na eletroquímica.
Não se conhecia esse conceito.
No começo do século XIX começaram a aparecer modelos teóricos que
explicavam o fenômeno da condutividade em eletrólitos.
Um dos primeiros modelos foi proposto por T. Grotthus em 1805
96
32
A medida fundamental para se estudar os
movimento dos íons em solução é a resistência
elétrica da solução.
Lei de Ohm
v
5
I =
As unidades são:
Georg Simon Ohm
1789-1854
vve
5w,xyz
I (A) =
97
Assim, pode-se definir
Resistência (R)
{
R α "
•
•
•
•
•
•
{
R = ρ "
L = comprimento
A = Área da seção de choque (eletrodo)
ρ = resistência específica ou resistividade
Unidade:
R (Ω) = ρ L (cm ou m)/A ( cm2 ou m2)
ρ = Ω cm ou Ω m
98
Condutância (C)
P
C = 5
P"
C =}{
inverso da resistência
P
k=}
"
C = k {
• K = condutância específica ou condutividade
• Unidades:
• C = Siemens (S)
– 1S = 1 Ω−1
• k = 1Ω−1 m−1
99
33
Condutividade de uma solução
A condutividade de uma solução depende do número de íons presente na
solução.
100
A condutividade de uma solução depende do
número de íons presente na solução.
Então a condutividade de soluções com
concentrações diferentes terão valores
diferentes
define-se a condutividade molar (Λ
Λm)
Λm =
l

onde c é a concentração molar da solução (mol L-1)
Unidade:
Λm
=
S m2 mol-1
101
Medida de condutância
A medida da condutância de um eletrólito é indireta,
propriedade determinada é a resistência
Célula de condutância: são recipientes
de vidro contendo dois eletrodos fixos
A solução eletrolítica célula de
condutância
Esquema de uma Célula de condutância
102
34
Exemplo:
Eletrodo e condutivímetro
103
Medida de condutância
célula de condutância circuito da ponte de Wheatstone
Os quatro ramos da ponte são:
• a célula de condutância,
• uma resistência variável
• xy
• yz
Circuito equilibrado resistência da
célula de condutância:
$CN j€
$
€
Charles Wheatston
1802-1875
104
Medidas de condutividade
e Constante de célula
)
M l
N
"
e
= Constante de célula
"
e
– medido com uma solução padrão; KCl
A = área do eletrodo
L = distância
105
35
Condutividade molar de soluções aquosas a 25 oC
Concentração
Mol L-1 a
0,0005
HCl
KCl
NaCl
H3CCOOH
422,7
147,8
124,5
-
0,001
421,4
147,0
123,7
48,63
0,005
415,8
143,6
120,7
22,80
0,01
412,0
141,3
118,5
16,20
0,02
407,2
138,2
115,8
11,57
0,03
399,1
133,4
111,1
7,36
0,10
391,3
129,0
106,7
5,20
Fonte: Handbook of Chemistry and Physics
106
-1
cm mol
2
350
300
condutividade molar (Λ)/ Ω
400
-1
450
HCl
KCl
NaCl
CH3COOH
250
200
150
100
50
0
0.00
0.02
0.04
0.06
0.08
0.10
-1
concentração / mol L
107
Através de medidas experimentais
Kohlrausch mostrou que em eletrólitos
fortes, há uma correlação entre a
condutividade molar ( Λ)e a concentração
do eletrólito (c).
Friedrich Wilhelm Kohlrausch
(1840-1910)
Λ Λ lP/8
0
Onde Λ é a condutividade em diluição infinita
quando
c0
Λ Λ0
κ − constante positiva para cada eletrólito
108
36
Λ Λ lP/8
• Método insatisfatório para eletrólitos fracos.
109
Condutividade molar em diluição infinita a 298K
Λ0 / S m-1 mol L-1
HCl
426,16
KCl
149,85
NaCl 126,45
KNO3 144,96
NaNO3 121,56
Λ Λ lP/8
110
A condutividade molar de um eletrólito varia com a concentração,
uma das possibilidades o número de íons em solução não é
proporcional à concentração do eletrólito.
Nesse sentido, os eletrólitos foram divididos em dois grupos:
eletrólitos fortes
eletrólitos fracos
Eletrólitos fortes encontram praticamente totalmente ionizadas em solução.
Como a ionização é praticamente completa, a concentração de íons em
solução é proporcional à concentração do eletrólito.
Eletrólitos fracos não estão completamente ionizados em solução.
A dependência entre a condutividade molar e a concentração vem do
deslocamento do equilíbrio de dissociação.
111
37
Teoria da Ionização
Em 1887, Arrhenius propôs a teoria da ionização,.
Quando coloca um eletrólito em solução, os
íons estão sempre em equilíbrio com
moléculas não ionizadas.
Svante August
Arrhenius,1887
Exemplo:
)* ⇌ B+ + A112
Quanto mais diluída a solução, o equilíbrio é deslocado
para a formação de íons
)* ⇌ B+ + A-
A condutividade de uma solução depende do número de
íons presente na solução,
[BA] 0
ocorre uma maior ionização;
[BA] 0
Λ Λ0
113
Λ0
Λ
=
=
condutividade
molar limitante em
diluição infinita
o número de
íons presentes
medida do
número total de
íons que pode ser
formado
em qualquer concentração
Podemos definir
Λ
Λ0 = α
Onde α = grau de dissociação.
114
38
Ostwald (1888) aplicou a lei de equilíbrio à ionização de eletrólitos
O eletrólito AB,
na concentração c
)* ⇌ B+ + A-
e uma fração de α de AB é ionizada
Então:
[AB] não ionizada é c (1-α); e
[ion] formado αc.
)* ⇌ B+
αc
c (1-α)
+
Aαc
115
)* ⇌ B+
c (1-α)
αc
+
Aαc
l A lei de equilíbrio químico
#
* ƒ) „
ƒ)*„
Onde k é a constante de equilíbrio.
Substituindo
[A+] = [B-] =
[AB] = c (1-α)
l αc αc
c (1−α)
αc
l α2c
(1−α)
lei de diluição
de Ostwald
116
Calculo do grau de dissociação, t
l α2c
(1−α)
l1 α α2c
l ,α α2c
α2c ,α # l 0
Duas soluções são possíveis.
Se α > 0
t ƒ l2 # 4l - k]/2c
se c 0 k ∞
eα1
Se a constante de dissociação é pequena e a concentração é relativamente elevada
K2 << 4Kc
t ≃
l

117
39
Kohlrausch eletrólitos com o mesmo cátion
ou mesmo ânion – apresentam um padrão:
Λ0(KCl) - Λ0 (NaCl) = 23,4
S
m-1/ mol L-1
Λ0(KNO3) - Λ0 (NaNO3) = 23,4
S
m-1/ mol L-1
118
Dados de condutância para vários eletrólitos
Eletrólitos
Λo/ Ω-1 cm2 mol-1
Diferença Λo/ Ω-1 cm2 mol-1
KCl
NaCl
149,86
126,45
23,41
KNO3
NaNO3
144,96
121,55
23,41
KI
NaI
150,32
126,91
23,41
Eletrólitos
Λo/ Ω-1 cm2 mol-1
Diferença Λo/ Ω-1 cm2 mol-1
KCl
KNO3
149,86
144,96
4,90
NaCl
NaNO3
126,45
121,55
4,90
½ BaCl2
½ Ba(NO3)2
139,94
135,04
4,90
119
Kohlrausch condutividade molar em diluição infinita
constituída de duas contribuições
• Uma do cátion
• Uma do ânion
Chamada de lei da migração iônica independente
Cada íon contribui para a condutividade molar limite total do
eletrólito
Essa lei pode ser escrita
como:
Λ0 = λο+ + λο−
Onde λο+ + λο− são as condutividades molares limites do cátion e do ânion respectivamente
120
40
Com essa lei, é possível calcular a condutividade limite de alguns íons individuais
Condutividade molar limite de cátions a 25oC
Cátions
λ +o/Ω-1 cm2 mol-1
H+
349,8
Na+
50,11
K+
73,52
Ag+
61,92
½ Mg2+
53,06
½ Ca2+
59,50
Condutividade molar limite de ânions a 25oC
ânions
λ -o/Ω-1 cm2 mol-1
OH-
197,6
Cl-
76,34
NO3-
71,44
½ SO4 2-
80,0
CH3COO-
40,9
I-
76,8
121
A lei da migração iônica independente
explica o padrão encontrado nas condutividades
dos eletrólitos com o mesmo cátion ou mesmo
ânion
Λ0 = λο+ + λο−
Λ0(KCl) Λ0(NaCl)= λο(κ+) + λο(Cl−) −λο(Na+)− λο(Cl−)
=
λο(κ+) −λο(Na+)
Λ0(KNO3) Λ0(NaNO3)= λο(κ+) + λο(ΝΟ3−) −λο(Na+)− λο(ΝΟ3−) = λο(κ+) −λο(Na+)
122
Condutividade molar de um íon
A condutividade molar de um íon
é a medida da quantidade de corrente que ele pode
transportar
corrente = velocidade de transferência
a comparação entre as condutividades molares de vários íons
condutividade molar com a mesma carga.
Isso é, para se comparar
Deve-se usar
λο(Na+) com + λο(Mg2+)
λο(Na+) com + λο(1/2 Mg2+)
Assim, podem ser comparadas condutividades molares equivalente de
transportadores de carga
123
41
Para comparar condutividades molares de quantidades
equivalentes de transportadores de carga
São válidas as seguintes relações:
Λo( ½ Mg2+) = ½ Λo(Mg2+)
Λo( 2 Cl-) = 2 Λo(Cl-)
Para comparar condutividades molares de íons que possuem a mesma carga:
dividir a condutividade molar pelo número de oxidação dessa quantidade de
íon
que é a condutividade equivalente.
Λo / z
Como o número de oxidação de um íon é adimensional a condutividade
iônica equivalente, terá as mesmas dimensões que a condutividade molar.
124
Exemplo
Λo( Ag+) = 61,92 Ω-1 cm2 mol-1
Λo( Ag+)/z = 61,92 Ω-1 cm2 mol-1
z=1
Λo( SO42-) = 160 Ω-1 cm2 mol-1
Λo( SO42-)/z = 80 Ω-1 cm2 mol-1
z=2
125
A migração independe dos íons.
Λo( ½ MgCl2) = Λo(½Mg2+) + Λo(Cl-) assim
Λo( ½ MgCl2) = 53,06 + 76,34
Λo( ½ MgCl2) = 129,40 Ω-1 cm2 mol-1
A equação de migração iônica independente deve ser escrita
como:
Λ0 = ν+λο+ + ν− λο−
Onde ν+ é o número de moles de cátions e
ν− é o número de moles de ânions
126
42
Mobilidade iônica
A condutância equivalente de uma solução depende da facilidade do movimento iônico
A velocidade iônica não é constante depende da intensidade do campo elétrico.
mobilidade iônica (u) é constante.
Mobilidade iônica é a velocidade iônica por unidade de campo elétrico
ˆ ‰
J
Devido a lei de migração iônica independente
ˆA ‰#
J
ˆ ‰
J
Onde v + é a velocidade do cátion e v - é a velocidade do ânion movendo-se em um campo elétrico
127
A mobilidade iônica está relacionada também com
condutância iônica equivalente em diluição infinita,
assim podemos escrever:
ˆA Š
#
4
ˆ Š
4
Onde F é a constante de Faraday; e Š
é a condutância iônica
equivalente em diluição infinita dos cátions e dos ânions.
Desta forma, podemos obter a mobilidade iônica dos íons em solução:
128
Com esses dados podemos realizar alguns cálculos de deslocamento de íons:
Calcule a condutância iônica a diluição infinda, a velocidade de
deslocamento e o tempo que o íon Cu2+ leva para sair de um eletrodo de
cobre e chegar ao outro eletrodo de cobre, a 298K.
Admita que o campo elétrico seja de 1 V cm-1,
Dados: F = 96500 C mol-1; u = 5,56 10-4 cm2s-1V-1
Š‹Œ 4. ˆ
129
43
Cálculo da condutância iônica
Š‹Œ 4. ˆ
Š‹Œ 96500M
N
1
. 5,56
Š‹Œ 96500M
N
10−4 cm2s−1V−1
1
. 5,56
Š‹Œ 56,654M
N
10−4 cm2s−1V−1
1
. cm2s−1V−1
Trabalhando com as unidades:
1 C/s = 1A
Š‹Œ 56,654M
N
A/V = Ω-1
1
. cm2s−1V−1
Š‹Œ 56,654)
N
1
. cm2V−1
Š‹Œ 56,654Ω−1
N
1
cm2
130
Cálculo da velocidade iônica
‰‹Œ J. ˆ
E = 1 V cm-1
u = 5,56 10-4 cm2s-1V-1
‰‹Œ 1 V cm−1 . 5,56 10−4 cm2s−1V−1
‰‹Œ 1 V cm−1 . 5,56 10−4 cm2s−1V−1
‰‹Œ 5,56 10−4 cm s−1
Tempo de deslocamento entre um eletrodo e o outro eletrodo (4cm)
dv = ds/dt
dt = 4 cm /5,56 10−4 cm s−1
dvdt = ds
dt = 7194,2 s
dt = ds/dv
 60
dt = 119,9 min
131
Condutância iônica equivalente e mobilidade iônica de alguns íons a 298K
Íons
Mobilidade iônica em
água a 298K
u/10-8 m2s-1V-1
Condutância
equivalente λo / Ω-1
cm2 mol-1
Li+
4,01
38,68
Na+
5,19
50,10
K+
7,62
73,50
Rb+
7,92
77,81
Cs+
7,96
77,26
Cu2+
5,56
53,6
Cl-
7,91
76,35
CH3COO-
4,24
40,90
SO42-
8,29
80,02
132
44
• Mobilidade iônica e condutância iônica
– Condutância é a medida da corrente que o
eletrólito pode conduzir
• A velocidade de transporte de carga depende
de
– 1) número de carga de cada íon
– 2) concentração de íons
– 3) velocidade dos íons
133
• Velocidade dos íons depende de:
– 1) intensidade do campo
– 2) viscosidade do solvente
– 3) efeito de assimetria
– 4) efeito eletroforético
Considerar – condutância em termos das velocidade dos íons
134
• Considerar:
– Uma solução de eletrólito de concentração c
– α é o grau de ionização
– c+ e c- concentrações de cátions e ânions
– E – campo elétrico
– v+ e v- velocidades dos cátions e ânions
135
45
• Dado um plano de superfície A, localizado no
interior da solução
A qualquer tempo t, o cátion do plano A percorre
a distancia v+ t
136
• O volume do bloco é v+ t . A
• A concentração de cátions é c+
• A quantidade de cátions no bloco é c+ v+ t A
• A carga transferida é
– Cátion c+ v+ t A z+ F
– Ânion c- v- t A |z-| F
137
A velocidade de transferência de carga é a corrente
– I+ - corrente transportada pelo cátion
– I- - corrente transportada pelo ânion
• A velocidade de transferência de carga é:
• I+ = c+ v+ A z+ F
e
I- = c- v- A |z-| F
• A corrente total e I
•
I = I+ + I• Então
• I = c+ v+ A z+ F + c- v- A |z-| F
138
46
• I = c+ v+ A z+ F + c- v- A |z-| F
• Se um mol de eletrólito dissocia em
– ν+ cátions
– ν- ânions
• c+ = ν+αc
e
c- = ν-αc
• I = ν+αc v+ A z+ F + ν-αc v- A |z-| F
• I = αcFA ( v+ z+ ν+ + ν- v- |z-|)
139
• Densidade de corrente j = i/A
• j = αcF ( v+ z+ ν+ + ν- v- |z-|)
v+= u+ E e
v- = u-E
• j = αcFE ( u+ z+ ν+ + ν- u- |z-|)
k = j/E
• k = αcF ( u+ z+ ν+ + ν- u- |z-|)
140
• k = αcF ( u+ z+ ν+ + ν- u- |z-|)
• Λ = k/c
• Λ = αF ( u+ z+ ν+ + ν- u- |z-|)
se α = 1 e
u+o u-o = mobilidade limite do cátion e do ânion
• Λo = F ( u+o z+ ν+ + ν- u-o |z-|)
141
47
• Λo = F ( u+o z+ ν+ + ν- u-o |z-|)
• Lei de migração independente: Λo = ν+ λ+o ν-λ-o
• Então: λ+o = u+o z+ F
•
λ-o = u-o |z-|F
142
• Número de transporte
• A corrente transportada pelos cátions e pelos
ânions é
I+ = c+ v+ z+ FA
I- = c- v- |z-| FA
• A corrente total é: I = c+ v+ z+ FA + c- v- |z-| FA
143
• O número de transporte do cátion (t+) é:
EA  A ‰ A  A 4)
 A ‰ A  A 4) #  ! ‰ ! | ! |4)
ou
EA  A‰A A
 A ‰ A  A 4) #  ! ‰ ! | ! |
144
48
• Como a velocidade dos íons se relaciona com
a mobilidade,
EA  AˆA A
 A ˆ A  A 4) #  ! ˆ ! | ! |
c+ = ν+c
c- = ν-c
EA tˆA ‰ A  A
tˆA ‰ A  A # tˆ! ‰ ! | ! |
EA ˆA‰ A A
ˆ A ‰ A  A # ˆ ! ‰ ! | ! |
145
• Em diluição infinita
EA ‰ A ŠA
‰ A ŠA # ‰ ! Š!
EA ‰ A ŠA
Λ
EA ‰ ! Š!
Λ
146
Essa variação do coeficiente de atividade de soluções diluídas é explicado pela
teoria de Debye-Hückel
A teoria de Debye-Hückel
A teoria de Debye-Hückel descreve o comportamento
termodinâmico das soluções eletrolíticas diluídas para eletrólitos fortes
relacionando o coeficiente médio de atividade com a força iônica do meio.
• Debye e Hückel consideraram que o afastamento da idealidade das
soluções diluídas eletrolíticas é atribuído às interações eletrostáticas de
longo alcance entre os íons.
•
não levaram em consideração as interações associadas às moléculas
do solvente. Eles consideraram o solvente como um meio contínuo cujo
único efeito é proporcionar um meio com um dado valor de constante
dielétrica.
147
49
Para o desenvolvimento da teoria, são levantadas algumas suposições:
1) Eletrólitos se dissociam completamente em íons em solução
2) As soluções são diluídas, com um concentração de 0,01 m ou mais baixas
3) Em média cada íon é circundado por íons de cargas opostas formando
uma atmosfera iônica
148
Debye e Hückel calcularam o potencial elétrico médio em cada íon, causado pela
diferença de outros íons na atmosfera iônica.
A energia de Gibbs dos íons foi então relacionada com o coeficiente de atividade
do íon individual.
Como não se pode medir o coeficiente de atividade dos cátions e dos ânions
individualmente, o resultado final é expresso em temos do coeficiente de atividade
iônica média do eletrólito
Lei limite de Debye-Hückel
log k” I é a força iônica
˜
1,824.106
| #  |√˜
•%–/8
1
ӏpp2
2
Onde mi e zi são as molalidade e a carga do íon no eletrólito, respectivamente
149
A Lei limite de Debye-Hückel permite calcular as concentrações iônicas para todos os
tipos de eletrólitos em uma base comum, de modo que não é preciso conhecer as
cargas dos íons individualmente.
em água e a 25 oC
(• = 78,54 e T = 298K)
Lei limite de Debye-Hückel
log k” 0509| #  |√˜
Em soluções com vários eletrólitos, todos contribuem para a força iônica,
entretanto, z+ e z- referem-se somente ao eletrólito para o qual k ” está sendo
calculado.
150
50
O gráfico mostra os valores calculados (curvas em azul)
e os valores medidos (curvas em vermelho)
de logk ” .
Gráfico de log k ”vs. √˜ para vários eletrólitos.
Observa-se que a lei limite se aplica a soluções diluídas mas em soluções
concentradas há desvios drásticos e a equação deve ser modificada
151
Aplicações das medidas de condutância
Determinação da condutividade molar limite
Eletrólitos fortes:
A condutividade molar limite de eletrólitos fortes pode ser determinada pela lei de
Kohlrausch.
Determina-se a condutividade em várias concentrações e constrói-se um gráfico de
condutividade vs raiz quadrada da concentração do eletrólito.
Λ Λ l P/8
152
Eletrólitos fracos:
Conhecidas as condutividades, em diluição infinita, molares limites dos
íons que constituem o eletrólito
a concentração molar limite pode ser determinada pela lei da
migração independente.
Λ0 = ν+λο+ + ν− λο−
Para o Calculo de Λ0 do ácido acético, por exemplo, podemos escrever:
Λ0 (CH3COOH) = λ0 (H+) + λ0 (CH3COO-)
Λ0 (CH3COOH) = 349,8 + 40,9
Λ0 (CH3COOH) = 390,07 Ω-1 cm2 mol-1
153
51
Eletrólitos fracos:
combinando os valores de condutividades de eletrólitos fortes
Λ0 (CH3COOH) = Λ0 (HCl) + Λ0 (CH3COONa) - Λ0 (NaCl)
substituindo-se os termos do lado direito da expressão por seus componentes
iônicos
Λ0 (CH3COOH) = Λ0 (HCl) + Λ0 (CH3COONa) - Λ0 (NaCl)
λ0 (H+) λ0 (Cl-) + λ0 (CH3COO-) + λ0 (Na+) - λ0 (Na+) - λ0 (Cl-)
λ0 (H+) λ0 (Cl-) + λ0 (CH3COO-) + λ0 (Na+) - λ0 (Na+) - λ0 (Cl-)
Λ0 (CH3COOH) =
λ0 (H+) + λ0 (CH3COO-)
Ácido clorídrico, acetato de sódio e cloreto de sódio, são todos eletrólitos
fortes.
154
Determinação da solubilidade de um sal pouco solúvel.
Se um sal pouco solúvel se dissociar de modo simples e completo em água,
pode-se determinar a solubilidade através das medidas de condutância
Determina-se a condutividade de uma solução saturada do sal,
Subtrai-se a condutividade do solvente
para ter como resultado somente a condutividade do sal:
k solução – k solvente = k sal
A condutividade molar foi definida como :
Assim pode-se usar a condutividade molar como:˚ Λ
l

lš(N

Onde Λs é a condutividade molar do sal na solução saturada e c é a concentração da solução
155
Se o sal for pouco solúvel, uma solução saturada deste sal pode ser
considerara como aproximadamente uma solução de diluição infinita, c 0
Lembrando que:
quando
c0
Λ Λ0
Λ0 = condutividade molar em diluição infinita
quando
Nesse caso
c0
Λs Λ0
Onde Λs é a condutividade molar do sal na solução saturada e c é a concentração da solução
c=
k sal
Λ0
Aplicando a lei de migração independente:
c=
k sal
ν+λο+ + ν λο
156
52
Exemplo:
A condutividade de uma solução saturada de cloreto de prata, a 25 oC, é 3,41x10-6
Ω −1 cm-1
A condutividade da água, a 25 oC, é 1,60x10-6 Ω −1 cm-1 (eletrólito fraco)
Sabendo ainda que a condutividade molar limite, a 25 oC,
dos íons Ag+ e Cl- são:
Ag+ λo = 61,92 Ω −1 cm-1 mol-1
Cl- λo = 76,34 Ω −1 cm-1 mol-1
Para calcular a solubilidade do AgCl:
Primeiro, determina-se a condutividade do AgCl, subtraindo contribuição da água
k solução – k solvente = k sal
k AgCl = 3,41.10-6 - 1,60.10-6
k AgCl = 1,81.10-6 Ω −1 cm-1
157
Aplicando a lei de migração independente:
c=
ν+λο+
k sal
+ ν λο
Substituindo os valores:
c=
1,81.10−6 Ω 1 cm−1
61,92 + 76,34 Ω 1 cm−1 mol−1
c=
1,81.10−6 Ω 1 cm−1
138,26 Ω 1 cm−1 mol−1
c = 1,31.10-5 mol L-1
c = 1,31.10-8 mol cm-3
x 1000
•
•
As limitações desse método são:
a concentração do sal dever ser baixa [solução saturada (sal
insolúvel)] para que condutividade molar possa ser considerada
como condutividade molar limite.
a dissolução do eletrólito deve ser simples e completa.
158
Considerando que a solubilidade de sal é pequena:
a concentração (c) pode ser considerada igual a
solubilidade (S)
Então a solubilidade do AgCl é: S (AgCl) = 1,3x10-5 Mol L-1
Como o AgCl se dissocia em Ag+ e ClKps = [Ag+][Cl-]
1,3x10-5x 1,3x10-5 mol
L-1
Kps = 1,69x10-10
159
53
Determinação da constante de dissociação
Procedimento simples para eletrólitos fracos.
Considerando um ácido fraco que se dissocia em água:
HA ⇄ H+ + AA constante de dissociação desse ácido é :
l( @
#
ƒ) „
ƒ@)„
Considerando uma solução
muito diluída: γ± = 1
160
α é o grau de dissociação do ácido, em uma
concentração c,
a constante de equilíbrio é
l( α2
1α
E como já foi definido, α =
›
›
Substituindo esses valores na equação chegamos al(: 1
1
1
Λ #
Λ0
Λ ,Λ02
Λ/Λ0)2c
(1−Λ/Λ0)
Lei de diluição de Ostwald
Λ02 Λ ,(
Λ0)
Λ
Essa equação resulta um gráfico linear de Λ vs 1/Λ de modo que o
coeficiente angular é ,(Λ02 e com coeficiente linear igual á ,(Λ0 .
Assim é possível determinar a constante de dissociação
161
Prof. Dr. Flavio Colmati IQ-UFG
determinar a constante de dissociação de um eletrólito fraco
A constante de dissociação do ácido HA é:l( @
#
ƒ) „
ƒ@)„
Isso quando a solução está muito diluída, mas rigorosamente a constante de dissociação é:
Ka = ka. Kγ
Onde Kγ é a contribuição do coeficiente de atividade, considerado igual a 1
quando a solução é muito diluída
γ
H+-A−
A equação pode ser re-escrita como: Ka = ka γ
HA
Para soluções diluídas o coeficiente de atividade das moléculas não-dissociadas,
HA tem valor próximo de 1
Assim a equação fica:
Ka = kaγH+-A−
162
54
Como os íons são univalentes (H+ e A-), os coeficientes de atividades são idênticos,
então:
Ka = ka γ2
Escrevendo essa equação na forma logarítimica
Log Ka = log ka + 2 log γ
O segundo termo dessa equação é dado pela lei de Debye-Hückel
log γ = −A ˜
Onde I é a força iônica, que é I = ½ (cH+ + cA-)
Se a concentração do ácido é c e o grau de dissociação é α, a concentração de
H+ e A- é αc
Então I = ½ (αc + αc ) que é
I = αc
163
I = αc
Substituindo da equação
log γ = −A ˜
log γ = −A αc
E a equação da constante de dissociação
Log Ka = log ka −2A αc
rearranjando
Log ka = 2A αc log Ka
Onde um gráfico de log Ka vs. αc é uma reta com coeficiente linear igual á log Ka
E o valor de log ka pode ser calculado por:l( t2 M
1 t
164
Titulação Condutimétricas
Quando se realiza uma titulação, as concentrações dos íons em solução variam.
Se essas variações levarem a uma variação na condutância final da solução
será possível acompanhar a titulação com medidas de condutância.
As principais aplicações são em titulações de ácido-base e titulações com formação de
precipitados
Para compreender os princípios da titulação condutimétrica, é
necessário conhecer a condutância dos íons.
165
55
Esses valores já são conhecidos:
Condutividade molar limite de cátions e ânions a 25oC
Cátions
λ +o/Ω-1 cm2 mol-1
Ânions
λ -o/Ω-1 cm2 mol-1
H+
349,8
OH-
197,6
Na+
50,11
Cl-
76,34
K+
73,52
NO3-
71,44
Ag+
61,92
½ SO4 2-
80,0
½ Mg2+
53,06
CH3COO-
40,9
½ Ca2+
59,50
I-
76,8
Observa-se que a condutividade molar limite da maioria dos íons está
entre 40 e 70 -1 cm2 mol-1. Exceto para os íons H+ e OHApesar das titulações não serem realizadas a diluição infinita, a maioria dos íons
apresentam condutâncias semelhantes. Exceto para os íons H+ e OH166
Analisando alguns casos em particular
Uma titulação de ácido forte – base forte: Considere uma titulação de ácido
clorídrico com hidróxido de sódio
Inicialmente a solução terá íons H+ e ClAo adicionar o NaOH, Na+ + OHOs hidróxidos se combinam com H+ e formam H2O, reduzindo a quantidade de íons H+ na
solução.
No final da titulação, haverá apenas íons Cl- e Na+
167
Conforme avança a titulação, a reação prossegue e a concentração de íons de H+ em
solução diminuem.
Os hidróxidos se combinam com H+ e formam H2O, reduzindo a quantidade de íons H+ na
solução.
No ponto final, (ponto de viragem) a solução contem apenas íons Na+ e
Cl- (desprezado a auto ionização da água).
A água é um eletrólito fraco e mesmo com a auto ionização, a
contribuição na condutividade é muito baixa e pode ser desprezada frente aos
outros íons em presente em solução.
No inicio da titulação íons H+ presente
Com o andamento da titulação, íons H+ são substituídos por íons Na+ condutividade da solução diminui
Após o ponto de viragem adição de íons OH- em excesso
Com o andamento da titulação, íons OH- ficam em excesso não solução
condutividade da solução aumenta
168
56
Um gráfico de condutância da solução vs. volume de NaOH
adicionado é possível verificar esse comportamento da
condutância da solução
Final da titulação
Excesso de íons
HOCom a adição de
NaOH após a
neutralização, há
excesso de íons
OH- em solução
(condutividade da
solução da
aumenta)
Inicio da titulação
Excesso de íons
H+
Com o decorrer da
titulação, íons H+
são substituídos
por íons Na+
(condutividade da
solução diminui)
Ponto de equivalência
169
Acido fraco – Base forte: Considere a titulação do ácido acético com NaOH
Inicialmente a solução terá íons H+ e CH3COOe moléculas não ionizadas de CH3COOH
Ao adicionar o NaOH, Na+
+ OH-
Os hidróxidos se combinam com H+ e formam H2O, reduzindo a quantidade
de íons H+ na solução. Da mesma forma íons de acetatos se combinam com íons de
+
170
Na
Conforme avança a titulação, a reação prossegue e a concentração de íons
de H+ em solução diminuem. Entretanto, como se trata de um ácido fraco:
Não há tantos íons H+ disponíveis em solução, como no caso do HCl,
o ácido fraco tende a ficar na forma não ionizada
Com andamento da titulação - Quando pouca quantidade de NaOH é
adicionada, os íons H+ em solução são substituídos pelos íons Na+.
A remoção dos íons H+ em solução provoca um aumento no grau de dissociação
do ácido acético (para regenerar o equilíbrio) – Aumenta a condutância
Com isso, ao adicionar o NaOH observa-se um aumento da condutividade da
solução devido a dissociação do ácido.
Após o ponto de equivalência, ao adicionar mais NaOH, a
condutividade da solução aumenta mais, devido ao excesso de íons OH- em
solução.
171
57
Um gráfico de condutância da solução vs. volume de NaOH
adicionado é possível verificar esse comportamento da
condutância da solução
Final da titulação
Excesso de íons
HO-
Inicio da titulação
Excesso de íons H+
Com o decorrer da
titulação, íons H+ são
substituídos por íons
Na+ mas desloca o
equilíbrio
aumentando a
dissociação do ácido
(condutividade da
solução aumenta)
Com a adição de
NaOH após a
neutralização, há
excesso de íons
OH- em solução
(condutividade da
solução da
aumenta)
Ponto de equivalência
172
Ácido fraco- base fraca:
Quando se titula ácidos com base fraca, o aspecto do gráfico , antes
de atingir o ponto de equivalência é similar ao obtido quando se usa uma base
forte
Porém, após o ponto de equivalência, o excesso de base
presente na solução estará na forma não ionizada (base fraca). A
presença de excesso de base não contribui significativamente para a
condutância da solução, então a condutância da solução permanece
praticamente constante.
ácido fraco – base fraca
A hidrólise do sal formado gera uma leve curvatura na curva (no ponto de
equivalência) dificultando a determinação. Se o ácido e a base forem muito fracos
não se observará o ponto de equivalência, somente uma leve curva em todo a
região que for realizado o experimento.
Aplicação para ácidos e bases com Ka e Kb superiores a 10-5
173
Acido forte
Base fraca
Base fraca
Ácido fraco
174
58
Mistura de ácidos:
Usando-se uma técnica condutimétrica é possível titular, com uma
base, uma mistura de ácido fraco e um ácido forte.
Adicionando-se a base à mistura de ácido:
A primeira reação é a substituição de
Íons H+ do ácido forte pelos cátions da base
175
A condutividade da solução diminui:
Depois de neutralizado o ácido
forte:
Neutralização do ácido forte
A adição da base Neutraliza o ácido fraco
A condutância da solução aumenta
Depois de neutralizado o ácido fraco a condutância da solução aumenta mais
rapidamente (se utilizado uma base forte)
176
José Vinicius Martins; Ana Paula Ruas de Souza; Maiara Oliveira Salles; Silvia Helena Pires
Serrano
Determinação de ácido acético em amostra de vinagre adulterada com ácido
clorídrico - um experimento integrado de titulação potenciométrica e
condutométrica
Quím. Nova vol.33 no.3, 2010
Neutralização
do ácido forte
Excesso de
base forte
Neutralização
do ácido
fraco
http://dx.doi.org/10.1590/S0100-40422010000300049
177
59
178
179
Elen Romão Sartori; Willian Toito Suarez; Orlando FatibelloFilho
Determinação condutométrica de cloridrato de metformina em
formulações farmacêuticas empregando nitrato de prata como titulante
Quím. Nova vol.32 no.7, 2009
180
60
Titulação por precipitação
É um método de titulação no qual se utiliza substâncias químicas que reagem entre
si e formam duas fases uma líquida e outra sólida e insolúvel no meio reagente
(normalmente, água), um precipitado, com isso é possível determinar
quantitativamente o produto da reação.
Considere a titulação de uma solução de cloreto de potássio com uma solução
de nitrato de prata.
:
Inicialmente a solução contem íons K+ e Cl-,
AgNO3
KCl
A reação é
No final da titulação, (desprezando a
pequena solubilidade do AgCl) a solução
contém íons nitrato e íons potássio
KCl + AgNO3 AgCl + KNO3
AgNO3
KCl
KCl
181
Antes do ponto final da titulação
Íons de cloreto são substituídos por íons de
nitrato
Ânions
λ -o/Ω-1 cm2 mol-1
OH-
197,6
Cl-
76,34
NO3-
71,44
½ SO4 2-
80,0
CH3COO-
40,9
I-
76,8
A condutividade entre o Cl- e NO3- não é muito diferente. Assim a condutividade
da solução será pouco afetada.
Após o ponto final da titulação, a adição de excesso de AgNO3 provoca
aumento do número de íons presente na solução, a condutividade da solução
aumenta.
182
Considere a titulação de uma solução de sulfato de magnésio com solução de
hidróxido de potássio
Com a reação, vão precipitar sulfato de bário e hidróxido de magnésio
MgSO4 + Ba(OH)2 Mg(OH)2 (s)+ BaSO4 (s)
Ba(OH)2
No inicio a solução contém íons magnésio e íons sulfato
MgSO4
A medida que a titulação prossegue, ambos são
retirados da solução por precipitação – a condutância
da solução diminui até o ponto final da titulação
Depois do final da titulação, o excesso de
Ba(OH)2 leva à solução íons Ba2+ e OH- - a
condutância da solução aumenta.
183
61