Critérios - Unisanta

Univesidade Santa Cecília
Engenharia Mecânica
Resistência dos Materiais II
Critérios de Resistência
Coeficiente de segurança
Tensão equivalente
Seja um ponto qualquer,
pertencente a um corpo em
equilíbrio, submetido a um estado
de tensões cujas tensões principais
estão representadas na figura 1.
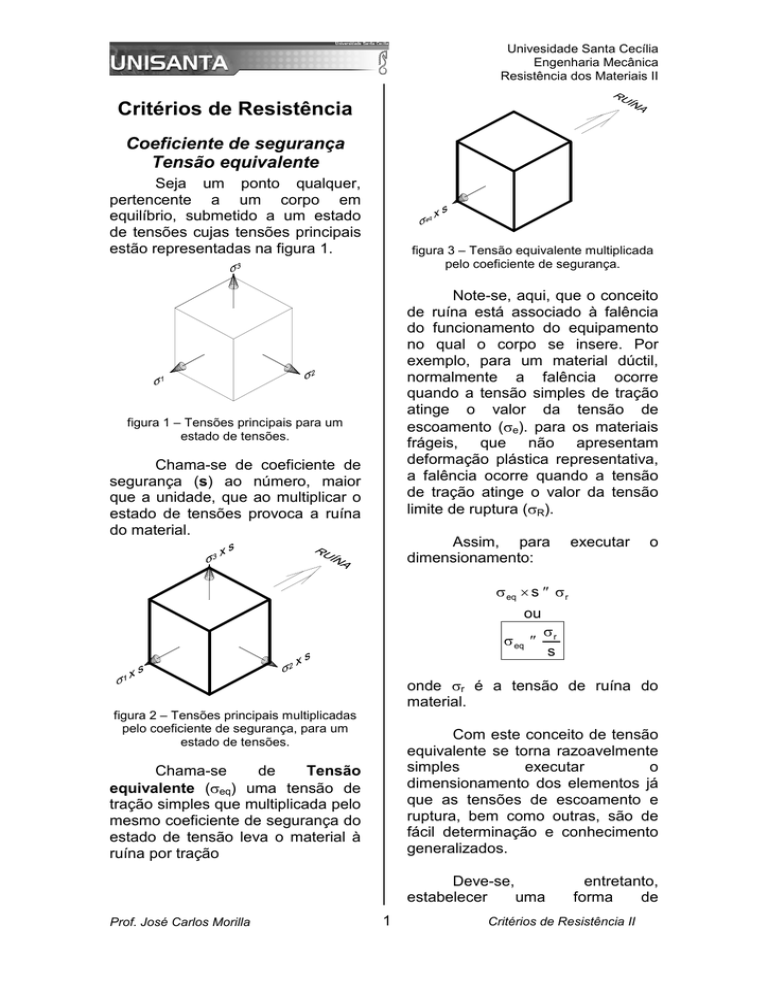
figura 3 – Tensão equivalente multiplicada
pelo coeficiente de segurança.
Note-se, aqui, que o conceito
de ruína está associado à falência
do funcionamento do equipamento
no qual o corpo se insere. Por
exemplo, para um material dúctil,
normalmente a falência ocorre
quando a tensão simples de tração
atinge o valor da tensão de
escoamento (σe). para os materiais
frágeis, que não apresentam
deformação plástica representativa,
a falência ocorre quando a tensão
de tração atinge o valor da tensão
limite de ruptura (σR).
figura 1 – Tensões principais para um
estado de tensões.
Chama-se de coeficiente de
segurança (s) ao número, maior
que a unidade, que ao multiplicar o
estado de tensões provoca a ruína
do material.
Assim, para
dimensionamento:
executar
o
σ eq × s ≤ σ r
ou
σ eq ≤
σr
s
onde σr é a tensão de ruína do
material.
figura 2 – Tensões principais multiplicadas
pelo coeficiente de segurança, para um
estado de tensões.
Com este conceito de tensão
equivalente se torna razoavelmente
simples
executar
o
dimensionamento dos elementos já
que as tensões de escoamento e
ruptura, bem como outras, são de
fácil determinação e conhecimento
generalizados.
Chama-se
de
Tensão
equivalente (σeq) uma tensão de
tração simples que multiplicada pelo
mesmo coeficiente de segurança do
estado de tensão leva o material à
ruína por tração
Deve-se,
estabelecer
uma
Prof. José Carlos Morilla
1
entretanto,
forma
de
Critérios de Resistência II
Univesidade Santa Cecília
Engenharia Mecânica
Resistência dos Materiais II
determinação da tensão equivalente
para que ela possa representar com
eficácia o estado de tensões
existente no ponto em estudo.
Critério da máxima tensão de
cisalhamento ou Critério de
Tresca.
Este critério se baseia no fato
que para os materiais dúcteis o
principal mecanismo de deformação
plástica é o de escorregamento nos
planos de maior densidade atômica.
Assim, a tensão equivalente (σeq) é
igualmente perigosa a um estado de
tensão quando ela apresentar a
mesma tensão de cisalhamento
máxima que o estado da tensão.
Critérios de
Dimensionamento.
Vários critérios diferentes, a
respeito da ruína dos materiais,
foram propostos ao longo do tempo:
1. Teoria da máxima tensão
normal proposta por Rankine;
2. Teoria
da
máxima
deformação normal, proposta
por Saint-Venant;
3. Teoria da máxima tensão de
cisalhamento, proposta por
Coulomb em 1773 e por
Tresca em 1868;
4. Teoria do atrito interno,
desenvolvida por Mohr e por
Coulomb;
5. Teoria da máxima energia de
deformação, proposta por
Beltrami em 1885;
6. Teoria da máxima energia de
distorção, desenvolvida por
Huber em 1904; Von Mises
em 1913 e Hencky em 1925;
7. Teoria da tensão octaédrica
de cisalhamento de Von
Mises e Hencky.
σ3
σ 2 σ1
σ
σ3 σ2
σeq
σ
figura 4 – Círculos de Mohr para um estado
de tensão e para uma tensão equivalente.
Sabendo-se que as tensões
de cisalhamento máxima nos dois
círculos de Mohr podem ser
determinadas por:
τ máx =
σ1 − σ 3
2
τ máx =
A igualdade
expressões fornece:
σ eq
das
2
(1)
duas
σ1 − σ 3 σ eq
=
2
2
Cada uma destas teorias propõe
um critério para a causa da ruína do
material.
σ eq = σ1 − σ 3
As experiências feitas em
tempos recentes mostram que,
entre as teorias apresentadas,
algumas são equivalentes e outras
são apenas de interesse histórico,
já que não apresentam resultados
compatíveis com os obtidos.
(2)
Critério da máxima energia de
distorção ou Critério de Von
Mises
Neste texto apresentar-se-á os
critérios baseados em algumas
destas teorias.
Prof. José Carlos Morilla
τmáx
τmáx
Este critério propõe que a
ruína
por
escoamento
seja
associada a valores críticos de certa
2
Critérios de Resistência II
Univesidade Santa Cecília
Engenharia Mecânica
Resistência dos Materiais II
porção da energia de deformação
do ponto material em estudo.
Quando as tensões principais
possuem valores diferentes, o cubo
que representa o ponto se
transforma em paralelepípedo. A
energia (U) para esta distorção é
dada por:
[
1+ ν
(σ1 − σ 2 )2 + (σ1 − σ 3 )2 + (σ 2 − σ 3 )2
U=
6 ×E
hidrostática (σ1=σ2=σ3), as tensões
equivalentes para os dois critérios
possuem valor igual a zero. Assim,
não é possível dimensionar nesta
situação por um destes critérios.
Critério de Coulomb-Mohr.
Este
critério
é
particularmente interessante para
materiais
que
apresentam
resistências
diferentes
quando
solicitados
à
tração
e
à
compressão.
Este
tipo
de
comportamento,
em
geral,
é
apresentado pelos materiais frágeis.
]
(3)
onde E é o módulo de elasticidade
do material e ν é o coeficiente de
Poison.
O mesmo fato acontece com
a tensão equivalente já que nesta
situação σ1= σeq e σ2 = σ3 =0. Para
a tensão equivalente, a energia de
distorção fica:
U=
A figura 5 mostra os dois
círculos de Mohr para a tensão de
ruptura à tração e à compressão de
um material frágil qualquer.
1+ ν
× 2 × σ 2eq (4)
6×E
Compressão
Tração
Igualando-se as expressões
3 e 4 tem-se:
σC
ou seja:
2
σ
figura 5 – Círculos de Mohr para um
material que resiste à tração e à
compressão.
(σ1 − σ 2 )2 + (σ1 − σ 3 )2 + (σ 2 − σ 3 )2 = 2 × σ 2eq
(σ1 − σ 2 )2 + (σ1 − σ 3 )2 + (σ 2 − σ 3 )2
σT
A proposição deste critério e
que os estados são igualmente
perigosos quando forem tangentes
à reta apresentada na figura.
= σ eq
(5)
A tensão equivalente para
este critério é:
OBS: Note-se que os dois critérios
apresentados levam em conta a
ductilidade do material e possuem
como tensão de ruína a tensão de
escoamento ou seja, valem apenas
para materiais com características
dúcteis.
onde
Note-se, também, que no
caso da solicitação chamada
σT= Limite de resistência à tração
σC= Limite de resistência à
Compressão
Prof. José Carlos Morilla
σ eq = σ1 − k × σ 3
k=
3
σT
σC
(6)
(7)
Critérios de Resistência II
Univesidade Santa Cecília
Engenharia Mecânica
Resistência dos Materiais II
A figura 6 é um gráfico
comparativo entre os critérios de
resistência apresentados.
No ponto A, indicado na
seção, atuam a máxima tensão
normal (σmáx) e a máxima tensão de
cisalhamento (máxτ) que valem:
σ máx =
M
W
máxτ =
T
Wt
(8)
Ao se isolar o ponto A, para
estudo, representando as tensões
que atuam no plano da seção, se
obtém:
Note-se aqui, que o critério
de Von Mises é aquele que mais se
aproxima
dos
resultados
experimentais.
Aplicação em eixos e vasos
de pressão.
Aplicação em Eixos
figura 8 – Ponto A com as tensões em seus
planos.
Uma
aplicação
muito
importante do que foi apresentado,
até
agora,
está
no
dimensionamento de eixos.
Observando-se a figura 8,
nota-se que o plano Q é um dos
planos principais. Isto é fato já que
a tensão de cisalhamento resultante
no plano é igual a zero.
Um eixo, nada mais é do que
uma barra circular submetida a um
esforço de flexão e um esforço de
torção. A figura 7 mostra uma barra
com seção transversal circular de
diâmetro “d”, solicitada por um
momento fletor M e um momento de
torção T.
No plano *, existe uma
tensão de cisalhamento que igual,
mas com sinal contrário, à tensão
de cisalhamento que atua no plano
da seção (O).
Assim, as tensões em cada
plano ficam:
Plano da seção (O):
M
T
σO =
τO =
(9)
W
Wt
Plano (*):
σ* = 0
figura 7 - barra circular solicitada por um
momento fletor e um momento de torção.
Prof. José Carlos Morilla
4
τ * = −τ O = −
T
(10)
Wt
Critérios de Resistência II
Univesidade Santa Cecília
Engenharia Mecânica
Resistência dos Materiais II
Plano (Q):
σQ = 0
σ2 = 0
τQ = 0
(11)
2
σ
σ
σ 
σ 3 = O − Raio = O −  o  + τ 2o
2
2
 2 
Com estes dados, é possível
construir o Círculo de Mohr para o
plano da seção (O) e o plano *. Isto
pode ser observado na figura 9.
Plano
το
σ3
σ2
(13)
Quando se dimensiona o eixo
pelo critério de Tresca, é possível
escrever:
σ eq = σ1 − σ 3
O
σ
σ1
σ eq =
σο
τ∗ =−το
σO
σ

+ Raio −  O − RAIO 
2
 2

σ eq = 2 × Raio
figura 9 – círculo de Mohr para o estado de
tensões.
(14)
Quando se substitui o valor
do RAIO na expressão 14 se
encontra:
A figura 10 mostra alguns
detalhes da figura 8.
2
Plano
το
σ3
σ2
σο σ1
σo/2
σ eq
O
σ 
= 2 ×  o  + τ o2  2 
σ eq = σ 02 + 4τ o2 (15)
σ
Quando se substitui as
expressões 9 na expressão 15, se
obtém:
Raio
figura 10 – detalhes do círculo de Mohr
para o estado de tensões.
2
σ eq
A figura 9 mostra que o raio
do círculo de Mohr entre σ1 e σ3 é:



2
(16)
Lembrando que para uma
seção circular:
2
σ 
RAIO =  o  + τ o2 (12)
 2 
πd3
πd3
W=
e Wt =
W t = 2W
32
16
(17)
Assim, as tensões principais
ficam:
2
σ
σ
σ 
σ1 = O + Raio = O +  o  + τ 2o
2
2
 2 
Prof. José Carlos Morilla
 T
M
=   + 4
W
 Wt
é possível escrever:
5
Critérios de Resistência II
Univesidade Santa Cecília
Engenharia Mecânica
Resistência dos Materiais II
2
M
 T 
σ eq =   + 4

W
 2W 
2
σ eq
2
σeq =
2
M  T 
=   +  W W
σ eq
σ eq
M2 + T 2
=
W
M2 + T 2
πd3
32
σ eq =
σ eq
expressão 20, a tensão equivalente
fica:
2
32 M2 + T 2
=
πd3
σ 
2
2 O  + 6(RAIO)
 2 
2
σ
=  O
 2
2

2
 + 3(RAIO)

(21)
Quando se substitui, na
expressão 21 a expressão 12, se
encontra:
σ
σ eq =  O
 2
2
 σ

 + 3  O
 2


2


 + τ O2  


(18)
σ eq = σ O + 3τ O2
2
O dimensionamento é feito
limitando-se a tensão equivalente
ao valor da tensão admissível à
tração; assim, se obtém:
Quando se substitui as
expressões 9 na expressão 22, se
obtém:
32 M2 + T 2
≤σ πd3
d≥3
32 M2 + T 2
πσ
2
σ eq
(19)
2
Ao se substituir o conteúdo
das expressões 13, se obtém:
σeq =
(23)
2
σ eq
M
 T 
=   + 3

W
 2W 
2
2
σ eq
3 T 
M
=   +   4W 
W
2
(20)
Quando são efetuados os
produtos
apresentados
na
Prof. José Carlos Morilla
2
é possível escrever:
2
2



πd3
πd3
W=
e Wt =
W t = 2W
32
16
(17)
(σ1 − σ 2 )2 + (σ1 − σ 3 )2 + (σ 2 − σ 3 )2
 σO

σ

2
+ RAIO  + (2 × RAIO) +  O − RAIO 

2
2




2
 T
M
=   + 3
W
 Wt
Lembrando que para uma
seção circular:
Quando o dimensionamento
é feito pelo critério de Von Mises, a
tensão equivalente fica:
σ eq =
(22)
σ eq =
6
M2 +
W
3 2
T
4
Critérios de Resistência II
Univesidade Santa Cecília
Engenharia Mecânica
Resistência dos Materiais II
σ eq =
M2 +
3 2
T
4
πd3
32
gases industriais. Outros exemplos,
mais comuns em nosso dia a dia
são os extintores de incêndio, os
balões, etc.
Vasos Cilíndricos
σeq =
3 2
T
4
32 M2 +
Tome-se um vaso cilíndrico
de parede fina que possui
comprimento l e diâmetro d, com
uma espessura de parede (e) muito
pequena em relação a este
diâmetro. Suponha que neste tubo
exista uma pressão interna p. Esta
pressão irá atuar no interior do tubo
de maneira a fazer com que exista
um crescimento em seu diâmetro e
um
crescimento
em
seu
comprimento.
Para que estas variações
ocorram,
é
necessário
que
apareçam tensões na parede do
vaso cujas direções são a do
comprimento (σ2) e a da tangente
ao perímetro médio da seção (σ1).
(24)
πd3
Lembrando, mais uma vez,
que o dimensionamento é feito
limitando-se a tensão equivalente
ao valor da tensão admissível à
tração; assim, se obtém:
32 M2 +
πd3
d≥
3
3 2
T
4
≤σ 32 M2 +
3 2
T
4
πσ
(25)
σ1
OBS:- Devemos observar que as
expressões (15) e (22) fornecem a
tensão equivalente, de acordo com
Tresca
e
Von
Mises,
respectivamente, para um ponto
qualquer onde atuam uma tensão
normal
e
uma
tensão
de
cisalhamento em um único plano.
σ2
σ1
figura 11 – tensões em um ponto da parede
de um vaso de pressão cilíndrico.
A figura 12 mostra um
diagrama de corpo livre para um
tubo de parede fina que possui uma
pressão interna p.
Aplicação em vasos de
pressão de parede fina
Os vasos de pressão são
considerados de parede fina
quando a espessura da parede for
tão pequena em relação ao seu
diâmetro que a distribuição de
tensões
normais
num
plano
perpendicular à superfície lateral
deste vaso é uniforme ao longo da
espessura da parede. Um bom
exemplo deste tipo de equipamento
são os vasos de pressão para
Prof. José Carlos Morilla
σ2
figura 12 – tensões na parede de um vaso
de pressão cilíndrico.
7
Critérios de Resistência II
Univesidade Santa Cecília
Engenharia Mecânica
Resistência dos Materiais II
Para determinar as tensões
que atuam na parede, se deve
lembrar que o conjunto das tensões
deve equilibrar o esforço produzido
pela pressão interna.
τmáx
σ3
Assim, tem-se:
p × d × l = 2 × (σ1 × e × l ) σ1 =
maneira,
Com estas tensões, a tensão
equivalente, de acordo com o
critério de Tresca fica:
é
σ eq = σ1 − σ 3 π × d2
σ2 × π × d = p ×
4
σ2 =
σ1
figura 14 – Círculo de Mohr para um ponto
da parede do tubo.
pd
(26)
2e
Da mesma
possível escrever:
σ2
σ
σ eq = σ1 =
pd
(28)
2e
De acordo com o critério de
Von Mises, se encontra:
pd
(27)
4e
Note-se aqui que estas
tensões são duas das tensões
principais que atuam nos pontos da
parede do tubo. Note-se, também,
que a tensão σ1 é igual ao dobro de
σ2. A terceira tensão principal (σ3) é
igual a zero.
σ eq =
(σ1 − σ 2 )2 + (σ1 − σ 3 )2 + (σ 2 − σ 3 )2
σ eq =
2
(σ1 − σ 2 )2 + (σ 1 )2 + (σ 2 )2 (29)
2
Lembrando que a tensão σ1 é
igual ao dobro de σ2 a expressão 29
fica:
Assim, as tensões que atuam
nos pontos da parede do tubo
podem ser representadas por:
σ eq =
(2σ 2 − σ 2 )2 + (2σ 2 )2 + (σ 2 )2
2
σ eq = σ 2 3
σ eq =
Vasos Esféricos
figura 13 – tensões principais para um
ponto da parede do tubo.
Tome-se um vaso esférico,
de parede fina, que possui diâmetro
d e espessura e.
O círculo de Mohr para estas
tensões fica:
Prof. José Carlos Morilla
pd
3 (30)
4e
8
Critérios de Resistência II
Univesidade Santa Cecília
Engenharia Mecânica
Resistência dos Materiais II
O círculo de Mohr para estas
tensões fica:
τmáx
σ2 σ1
σ3
figura 15 – tensões na parede de um vaso
de pressão esférico.
figura 17 – Círculo de Mohr para um ponto
da parede da esfera.
As tensões nos pontos da
parede de um vaso de pressão
esférico, possuem o mesmo valor,
em qualquer que seja a direção
tomada. Ou seja:
σ× π×d = p×
σ=
σ
Com estas tensões, a tensão
equivalente, de acordo com o
critério de Tresca fica:
σ eq = σ1 − σ 3 π × d2
4
σ eq = σ =
pd
(32)
4e
De acordo com o critério de
Von Mises, se encontra:
pd
(31)
4e
Note-se aqui que estas
tensões são duas das tensões
principais que atuam nos pontos da
parede da esfera. Note-se, também,
que a tensão σ1 é igual a σ2. A
terceira tensão principal (σ3) é igual
a zero.
σ eq =
(σ1 − σ 2 )2 + (σ1 − σ 3 )2 + (σ 2 − σ 3 )2
2
σ eq =
(σ1 )2 + (σ 2 )2 (33)
2
Lembrando que a tensão σ1 é
igual a σ2 a expressão 33 fica:
Assim, as tensões que atuam
nos pontos da parede do tubo
podem ser representadas por:
σ eq =
2(σ 1 )
2
2
σ eq = σ
σ eq =
Importante observar que,
para este tipo de vaso de pressão, a
tensão equivalente é a mesma
pelos
dois
critérios
de
dimensionamento.
figura 16 – tensões principais para um
ponto da parede da esfera.
Prof. José Carlos Morilla
pd
(34)
4e
9
Critérios de Resistência II