ex - Centro de Estudos Espaço

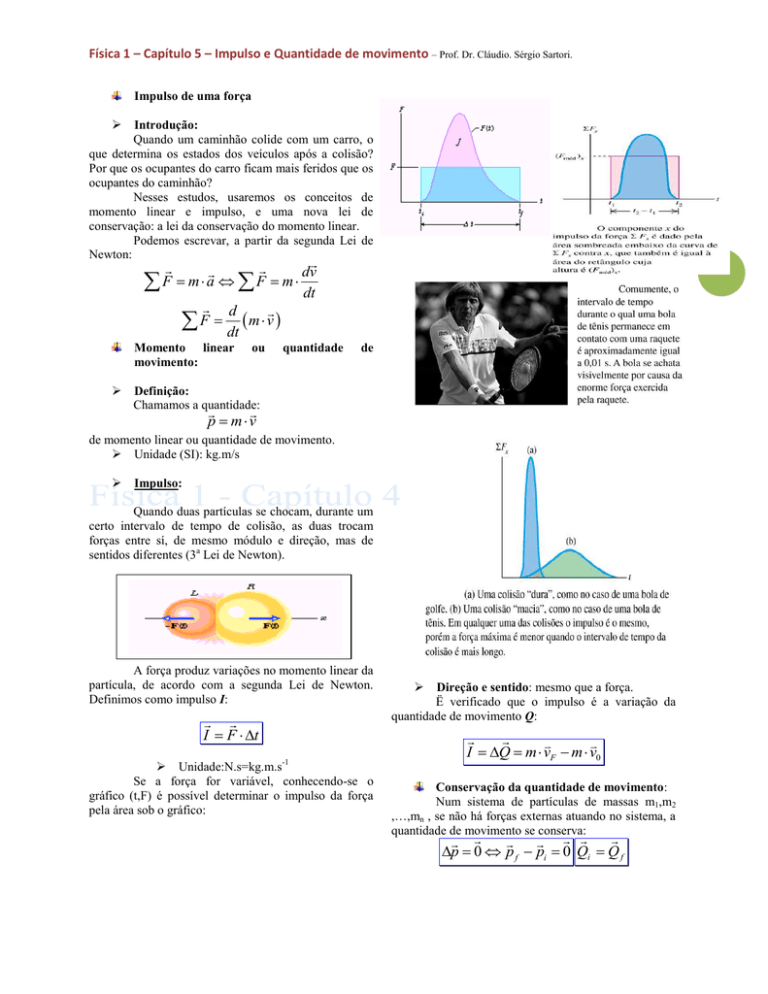
Física 1 – Capítulo 5 – Impulso e Quantidade de movimento – Prof. Dr. Cláudio. Sérgio Sartori.
Impulso de uma força

Introdução:
Quando um caminhão colide com um carro, o
que determina os estados dos veículos após a colisão?
Por que os ocupantes do carro ficam mais feridos que os
ocupantes do caminhão?
Nesses estudos, usaremos os conceitos de
momento linear e impulso, e uma nova lei de
conservação: a lei da conservação do momento linear.
Podemos escrevar, a partir da segunda Lei de
Newton:



dv

 F  m  a   F  m  dt
 d

 F  dt  m  v 
Momento linear
movimento:

ou
quantidade
1
de
Definição:
Chamamos a quantidade:


p  mv
de momento linear ou quantidade de movimento.
 Unidade (SI): kg.m/s

Impulso:
Quando duas partículas se chocam, durante um
certo intervalo de tempo de colisão, as duas trocam
forças entre sí, de mesmo módulo e direção, mas de
sentidos diferentes (3a Lei de Newton).
A força produz variações no momento linear da
partícula, de acordo com a segunda Lei de Newton.
Definimos como impulso I:
 
I  F  t
 Unidade:N.s=kg.m.s-1
Se a força for variável, conhecendo-se o
gráfico (t,F) é possível determinar o impulso da força
pela área sob o gráfico:

Direção e sentido: mesmo que a força.
Ë verificado que o impulso é a variação da
quantidade de movimento Q:




I  Q  m  vF  m  v0
Conservação da quantidade de movimento:
Num sistema de partículas de massas m1,m2
,…,mn , se não há forças externas atuando no sistema, a
quantidade de movimento se conserva:

 

  
p  0  p f  pi  0 Qi  Q f
Física 1 – Capítulo 5 – Impulso e Quantidade de movimento – Prof. Dr. Cláudio. Sérgio Sartori.
 Exemplo 1 - Determine o vetor quantidade de
movimento das partículas nas situações (a) e (b).
 Exemplo 4 – Determine a variação da
quantidade de movimento da bola.
2



p  m  v f  m  vi


p  m  20  iˆ  m  30  iˆ

p  50m  iˆ

 Exemplo 5 – A massa de uma bola de futebol é
0.4 kg. Determine o impulso da força resultante e a
força resultante média para o caso da bola sabendo que
inicialmente a bola se desloca da direita para a esquerda
com 20 m/s e após o chute, de interação 0.01s, desloca
com módulo 30 m/s fazendo um ângulo de 45° com a
horizontal.

Exemplo 2 - Canhão disparando uma bala. A
velocidade de recuo do canhão é:
mb  vb  M V  0  V 
m
vb
M

Solução:
v f x  v f  cos 45  v f x  30  cos 45
v f x  30  0.707  v f x  21.21
v f y  v f  sen45  v f y  30  sen45

Exemplo 3 - Bomba explodindo em 3
fragmentos.
v f y  30  0.707  v f y  21.21



p  m  v f  m  vi
px  m  v f x  m  vix
px  21.2  0.4   20  0.4   px  16.48
p y  m  v f y  m  viy  p y  8.48
kg  m
s
kg  m
s
Física 1 – Capítulo 5 – Impulso e Quantidade de movimento – Prof. Dr. Cláudio. Sérgio Sartori.

Fmed
px

F


med

x
p
t


p y
t
F
med y 
t


 Fmed x  1650 N

F
 850 N

 med y
2
2
Fmed  Fmed
 Fmed
x
y
Fmed  1.9 103 N
3
Direção:
  arctg
Fmed y
Fmed x
   arctg
850
1650
  27

Exemplo 6 – Um atirador manteém
um rifle de 3 kg segurando-o frouxadamente de
modo que ele possa recuar livremente ao disparar.
Ele atira uma bala de massa mB = 5.00 g
horizontalmente com velocidade relativa ao solo
dada por vB = 300 m/s. Qual é a velocidade de
recuo do rifle vR e qual o valor da energia cinética
final e do momento final da bala ? E do rifle?

Solução


 
p f  pi  0  mb  vb  iˆ  mR  vR  iˆ  0
mb  vb
m
 vR  0.500
mR
s
vR 
Colisões:
Definimos coeficiente de restituição como a
razão entre a velocidade relativa de afastamento e a
velocidade relativa de aproximação:
e
vraf
v rap
 0  e 1
As colisões de corpos podem ser classificadas
em:
1. Elásticas. Nesse caso a energia mecânica se
conserva: E M i  E M F e o coeficiente de restituição é
igual a 1 (e = 1).
2. Inelásticas.
(parcialmente
elásticas
(0<e<1)). A energia mecânica não se conserva. Quando
e = 0, ou seja, dois corpos após se colidirem saem com a
mesma velocidade, chamamos de colisão perfeitamente
inelástica. Neste caso há uma máxima perda de energia
cinética. Essas perdas de energia são devidas a
transformações em outras formas de energia, como por
exemplo em energia térmica e sonora.
Como exemplo citamos as colisões em duas
dimensões ilustradas a seguir:
Física 1 – Capítulo 5 – Impulso e Quantidade de movimento – Prof. Dr. Cláudio. Sérgio Sartori.
 Exemplo 7 – Encontre a velocidade final do
cavaleiro A. Não há atrito nos trilhos. Suponha
coeficiente de restiruição e = 1 (choque perfeitamente
elástico).
4

Solução


p f  pi

mA  vA1  iˆ  mB  vB1  iˆ  mB  vB2  iˆ  mA  vA2  iˆ
0.5  2  iˆ  0.3  2  iˆ  0.3  vB2  iˆ  0.5  vA2  iˆ
1 iˆ  0.6  iˆ  0.3  vB2  iˆ  0.5  vA2  iˆ
0.4  0.3  vB2  0.5  vA2
e
e
vB2  vA2
22
vrafastamento
vraproximação
1
vB2  vA2
4
vB2  vA2  4
1

0.3  vB2  0.5  vA2  0.4

vB2  vA2  4


0.2  vA2  0.4  0.3  4  0.2  vA2  0.8
m
s
m
vB2  8
s
vA2  4
 Exemplo 8 – Dois blocos de gelo deslizam
sobre a superfície sem atrito de um lago congelado
conforma a figura. O bloco A, com massa mA = 5.0 kg se
move com velocidade vA1 = 2.0 m/s paralelamente ao
eixo Ox. Ele colide com o bloco B, de massa mB = 3.0
kg que está inicialmente em repouso. Depois da colisão,
verifica-se que a velocidade do bloco A é dada por vA2 =
1.0 m/s com uma direção que faz um ângulo  com a
direção inicial. Qual é a velocidade final do bloco B?
Quais os ângulos  e ?
Solução


p f  pi
mA  vA1  iˆ  mA  vA2  cos   iˆ  mA  vA2  sen  ˆj  mB  vB2  cos   iˆ  mB  vB2  sen  ˆj
mA  vA1  mA  vA2  cos   mB  vB2  cos 

 0  mA  vA2  sen  mB  vB2  sen
1
1
1
EM antes  EM depois  mA  vA21  mA  vA22  mB  vB22
2
2
2
2
2
m

v

m

v
A
A1
A
A2
vB22 
mB
m
vB2  4.47
s
0.5  4  0.5  2  cos   0.3  4.47  cos 

 0  0.5  2  sen  0.3  4.47  sen
cos   1.341 cos   2

 sen  1.341 sen  0
cos   2 1.341 cos 
sen  1.341 sen
sen2  cos2   1
 1.341 sen    2 1.341 cos  
2
2
1
1.79828  sen   4  2  2 1.341 cos   1.7982  cos2   1
2
 2

1.79828   sen
  cos2    4  5.364  cos   1
  

1

1.79828  4  5.364  cos   1
5.364  cos   1  5.79828
4.79828
cos  
 cos   0.8945
5.364
  arccos0.8945    26.56
sen  1.341 sen  1.341 1  cos2 
sen  1.341 1  0.89452
sen  0.5995    arcsen  0.5995
  36.9
Física 1 – Capítulo 5 – Impulso e Quantidade de movimento – Prof. Dr. Cláudio. Sérgio Sartori.
 Exemplo 9 – Em um teste de choques de
automóveis, um carro colide com uma parede,
aproximando dela com uma velocidade
m

vi  15  iˆ
s
. Após a colisão, o carro de 1500 kg possui velocidade
m

v f  2.6  iˆ . Se a colisão dura 0.15 s, calcule o
s
impulso e a força que a parede exerce sobre o carro.
Suponha mb = 5 g, mB = 1 kg e h = 5 cm. Encontre:
(a) a velocidade inicial da bala.
(b) a perda de energia.

Solução:
Antes do choque: energia cinética:
mb  vb2
Ei  Eb  EB 
2
Após o choque:
Ef 
 mb  mB   v 2f
2
Conservação da quantidade de movimento:
mb  vb   mb  mB   v f
vf 

Solução:

 





I  p  I  p f  pi  I  m  v f  m  vi

I  1500  2.6  iˆ  1500  15  iˆ

I  2.64 104  iˆ  N  s 
 p
 2.64 104  iˆ
F
F
t
0.15

5 ˆ
F  1.76 10  i  N 




 Exemplo 10 – Um pêndulo balístico é um
sistema utilizado para medir a velocidade de um projétil
como uma bala. Na figura, a bala penetra em um bloco
de madeira suspenso por fios e se aloja no bloco de
madeira; o conjunto se eleva a uma altura h e a colisão é
inelástica.
mb
 vb
mb  mB
Conservação da energia entre o instante após o
choque e o momento do sistema atingir a altura
máxima:
EM i  EM f 
 mb  mB   v 2f
  mb  mB   g  h
2
vf  2 g  h
vf 
mb
 vb
mb  mB
 m  mB
vb   b
 mb
 0.005  1 
vb  

 0.005 

 2 g h

2  9.81 0.05
m
s
E  E f  Ei
vb  199
E 
 mb  mB   v 2f
2
E  98.5J
mb  vb2

2
 Exemplo 11 – Um bloco de massa m1 = 1.60
kg inicialmente movendo-se para a direita com
velocidade 4.00 m/s em um piso sem atrito, colide com
uma mola presa a um segundo bloco de massa m2 = 2.10
kg inicialmente movendo-se para a esquerda com
velocidade de 2.50 m/s. A mola tem constante elástica
600 N/m.
(a) No instante que o bloco 1 move-se para a
direita com velocidade 3.00 m/s, determine a velocidade
do bloco 2.
5
Física 1 – Capítulo 5 – Impulso e Quantidade de movimento – Prof. Dr. Cláudio. Sérgio Sartori.
(b) Determine o valor de x nesse instante.
(contido na água pesada, D2O) ou carbono (contido na
grafite). Mostre que os nêutrons podem perder a maior
parte de sua energia cinética se as colisões forem
elásticas entre o material moderador.


Solução:
Massa do material moderador inicialmente em
repouso: mm.
Velocidade inicial do nêutron: vni.
Solução:
Conservação do momento:
Eni 
m1  v1i  m2  v2i  m1  v1 f  m2  v2 f
m
v2 f  1.74
s
En f 
Conservação da energia mecânica:
i
2

m2  v 22
i
2

m1  v12
f

m2  v 22
f
2
x  0.173m
2
2
2
m  m  mm  2
 En f  n  n
 vn
2  mn  mm  i

k  x2
2
mn  mn  mm  2

 vn
En f
2  mn  mm  i
fn 
 fn 
mn  vn2i
Eni
2
2
 m  mm 
fn   n

 mn  mm 
mm  vm2 f
Em f 
2
 2mn 
vm f  
  vni
 mn  mm 
 Exemplo 12 – Suponha uma colisão elástica
entre as duas partículas mostradas na figura.
Mostre, aplicando a conservação da energia e a
conservação do momento, que:
 m  m2 
v1 f   1
  v1i
 m1  m2 
2m1
v2 f 
 v1
m1  m2 i
 Exemplo 13 – Em um reator nuclear, nêutrons
são produzidos quando um átomo
2
2
Ei  E f
m1  v12
mn  v
2
nf
mn  vn2i
235
92
U divide-se em um
processo conhecido como fissão. Estes nêutrons estão se
movendo com velocidade da ordem de 107 m/s e sua
velocidade é reduzida para 103 m/s antes de tomarem
parte em outro processo de fissão. Sua velocidade é
reduzida porque passam por um material sólido ou
líquido, chamado de moderador, no qual envolvem
colisões elásticas entre núcleos leves, como o deutério
 2mn 

mm  
  vni 
 mn  mm 

Em f 
2
2mm  mn2
Em f 
 vn2i
2
 mn  mm 
2
A fração fm da energia cinética inicial
transferida para o núcleo moderador será:
fm 
Em f
Eni
 fm  4
mm  mn
 mn  mm 
2
 Exemplo 14 – Efeito da atiradeira
gravitacional. A figura mostra o planeta Saturno
movendo-se em sentido x negativo com uma velocidade
orbital em relação ao Sol de 9.6 km/s. A massa de
Saturno é 5.69.1026kg. Uma nave espacial de massa 825
kg se aproxima de Saturno com velocidade de 10.4
km/s. A atração gravitacional de Saturno (uma força
conservativa) faz com que a nave mude de direção e
retorne em sentido oposto. Calcule a velocidade final da
6
Física 1 – Capítulo 5 – Impulso e Quantidade de movimento – Prof. Dr. Cláudio. Sérgio Sartori.
nave depois que ela afasta de modo que não sinta mais a
força gravitacional de Saturno.
 Exemplo 16 – Colisão de carros num
semáforo. Um carro de 1500 kg e 25m/s colide com
outro de 2500kg indo para o norte a 20 m/s como
mostra a figura.
7
 Solução: Nesse caso, a ― colisão‖ não é um
impacto, mas sim uma interação gravitacional. Seja A a
nave espacial, B o planeta Saturno. Suponto que a
velocidade do planeta saturno seja constante durante a
interação: imagine o problema como uma colisão
elástica em linha reta na qual: vB1 = vB2 = 9.6 km/s e vA1
= 10.4 km/s. Assim:
e 11
1
vA2  vB2
vA1  vB1
vrafastamento
vraproximação
 vA1  vB1  vA2  vB2
vA2  vA1  vB1  vB2
vA2  10.4  9.6  9.6  vA2  29.6
km
s
 Exemplo 15 – Dispositivo anti-strees.
Choques elásticos (e = 1). Air Bag – Choque
perfeitamente inelástico (e = 0).
Encontre a direção e a velocidade dos carros
após a colisão, supondo choque perfeitamente
inelástico (e = 0; carros permanecem juntos).

Solução:
e00
p
xi
vrafastamento
vraproximação
 v1 f  v2 f
  px f  m1  v1   m1  m2   vF  cos 
1500  25  1500  2500  vF  cos
37500  4000  vF  cos 
 p  p
yi
yf
 m2  v2   m1  m2   vF  sen
50000  4000  vF  sen
50000 4000  vF  sen
50

 tg 
37500 4000  vF  cos 
37.5
50
  arctg
   53.1
37.5
37500
37500
vF 
 vF 
4000  cos 
4000  cos 53.1
m
vF  15.6
s
Física 1 – Capítulo 5 – Impulso e Quantidade de movimento – Prof. Dr. Cláudio. Sérgio Sartori.
 Exemplo 17 – Colisões de partículas. Dois
prótons colidem de forma que o próton 2 está
inicialmente em repouso e o 1 possui velocidade 3.5.10 5
m/s. Depois da colisão, o próton 1 move-se com
velocidade formando um ângulo de 37° com o eixo x e o
próton 2 com velocidade formando um ângulo .
Encontre a velocidade final dos dois prótons e o ângulo
.

Solução:
p
xi
hospitais usam hoje em dia para detectar o cancro já sem falar nos
avanços técnicos necessários e exigidos pelas experiências, técnicas
que acabam sempre no domínio público, como aliás todas as
descobertas feitas no CERN.
  px f
8
mp  v1  mp  v1 f  cos37  mp  v2  cos 
3.5 105  v1 f  cos37  v2  cos 
 p  p
yi
yf
0  mp  v1f  sen37  mp  v2 f  sen
v1 f  sen37  v2 f  sen
Conservação da energia:
Ei  E f  v12f  v22f   3.5 106 
2
Resolvendo o sistema:
m
s
m
v2 f  2.11105
s
  53
v1 f  2.8 105
Observe que quando duas massas iguais
colidem elasticamente (com uma delas em repouso
inicialmente: +θ=90°
Adaptado e Extraído de:
http://pt.wikipedia.org/wiki/Organiza%C3%A7%C3%A3o_Europeia_
para_a_Investiga%C3%A7%C3%A3o_Nuclear
O acrónimo CERN provem do francês "Conseil Européen
pour la Recherche Nucléaire" (Conselho Europeu para Investigação
Nuclear) , um organismo provisório instituído em 1952 e criada com o
apoio da UNESCO, e que tinha por objectivo no fim da segunda
guerra mundial "promover a colaboração entre Países Europeus na
área da investigação no domínio da Física da Altas Energias (FAE)".
Quando em 1954 foi rectificada a convenção pelos 11 países
fundadores (ver: Países Membros) o 'Conselho' deu origem à
'Organização' mas manteve-se o acrónimo. Como nessa altura a
pesquisa da física fundamental tinha por principal objectivo a
compreensão do interior do átomo, o núcleo atómico, isso explica o
termo 'nuclear' empregue, mas pela imagem belicosa desta palavra o
CERN chamou-se numa dada altura "Organização Européene pour la
Physique des Particules".
Desde a sua criação, o CERN foi importante para aproximar os povos,
e foi mesmo o único local onde cientistas norte-americanos e russos
trabalharam juntos durante a Guerra Fria. Além disso certas
experiências e detectores do CERN estão na base de aparelhos que os
Para as sua experiências o CERN necessita, à partida,
de hidrogénio e de chumbo, pois que os prótons são produzidos a
partir de atomos de hidrogénio dos quais se extrai os elétrons. Os
protões começam o seu percurso num acelerador linear, o LINAC
e depois são injectados sucessivamente no injector do síncrotron
sincrotão a prótons do PS, o PSB sigla inglesa de 'PS Booster', no
Super Síncroton de Prótons (SPS) antes de chegarem ao Grande
Colisor de Hadrons (LHC).
- os íons de chumbo são produzidos a partir de chumbo vaporizado
antes de serem enviados no LINAC 3. Em seguida acelerados no Low
Energy Ion Ring (LEIR) e seguem o mesmo trajecto que os protões.
O CERN emprega nas suas instalações um conjunto de 6
aceleradores. Cada um tem por finalidade aumentar a energia do feixe
das partículas recebidas antes de as enviar a experiências ou a um
outro acelerador.
Física 1 – Capítulo 5 – Impulso e Quantidade de movimento – Prof. Dr. Cláudio. Sérgio Sartori.
Assim, e no caso de entrarem em colisão à velocidade da luz no LHC,
as partículas passam do duoplasmatron de 90 keV, ao RFQ de 750
keV, ao Linac 2 de 50 MeV, ao Síncroton Injector do PS o (PSB) de
―PS Booster‖ de 1,4 GeV, ao Sincrotrão a Protões (PS) de 25 GeV e
finalmente ao Super Síncroton de Prótons (SPS) de 450 GeV e
finalmente no LHC 3,5 TeV .
Em contrapartida no AD, o Desacelerador de Antiprótons, reduz-se a
velocidade para estudar 'calmamente' a antimatéria.
Fora do campo científico o CERN é principalmente
conhecido por ter sido o berço da invenção da World Wide Web, ou
simplesmente WWW ou Web. Corria o ano de 1990, e o que, numa
primeira fase, permitia apenas aos cientistas trocar dados, acabou por
tornar-se na complexa e essencial Web.
Tim Berners-Lee que tinha construido o seu primeiro
computador na Universidade de Oxford, onde se formou em 1976
tornava-se, quatro anos mais tarde, consultor de engenharia de
software no CERN e escrevia o seu primeiro programa para
armazenamento de informação – chamava-se Enquire e, embora nunca
tenha sido publicada, foi a base para o desenvolvimento da Web.
Na sua proposta para o projecto em 1989 - é curioso ver o comentário
do seu chefe de serviço- sugere a ideia de hipertexto que permite às
pessoas trabalhar em conjunto, combinando o seu conhecimento
através uma rede de documentos ligados entre si. Foi esse projecto que
ficou conhecido como a World Wide Web. Para a sua realização T.
Berners-Lee foi ajudado tanto na expecificação da linguaguem
HTML, do navegador, assim como no criação do servidor Web por
Robert Cailliau. A Web funcionou primeiro dentro do CERN, e no
Verão de 1991 foi disponibilizada mundialmente.
Em 1994 Berners-Lee criou o World Wide Web
Consortium, onde actualmente assume a função de director. Mais
tarde, e em reconhecimento dos serviços prestados para o
desenvolvimento global da Web, foi nomeado cavaleiro pela rainha da
Inglaterra.
 Solução: Análogo ao anterior.
θ = 55°
Centro de Massa
Ao trabalharmos com corpos com dimensões
não desprezível é de extrema importância localizar o
centro de massa desse corpo. Estudamos o movimento
do corpo no centro de massa, pois esse terá um
comportamento de um ponto no qual toda massa do
corpo está localizada nele. Veja exemplo abaixo.
9
Pode-se associar a um sistema de partículas um
determinado centro de massa, no qual se aplica a 2 a Lei
de Newton:


Fext  M  acm
Para calcular a posição do centro de massa de um
sistema de n partículas de massas m1,m2,m3..,mn , basta
fazer:




m1r1  m2 r2  m3 r3    mn rn

rcm 
m1  m2  m3    mn
 Exemplo 18 – Bilhar. Em um jogo de bilhar,
deseja-se colocar uma bola no canto, como mostra a
figura.




m1v1  m2 v2  m3 v3    mn vn

vcm 
m1  m2  m3    mn




m a  m2 a 2  m3 a3    mn a n

acm  1 1
m1  m2  m3    mn
As expressões para velocidade e aceleração do
CM são obtidas derivando a primeira relação com
respeito ao tempo.
Encontre o ângulo θ. Despreze efeitos de
rotação e de atrito.
Física 1 – Capítulo 5 – Impulso e Quantidade de movimento – Prof. Dr. Cláudio. Sérgio Sartori.
Determinação Experimental do Centro de
massa.


 Exemplo 19 – Determine o centro de massa do
sistema da figura:
10
Solução:
(a)
m dm
m

 dm  dx
L dx
L
1
xcm   xdm
m
L
1 m
xcm   xdx
m0 L
L
1 m
1 x2
xcm 
xdx 
m L 0
L 2
xL
x 0
L
xcm 
2
(b)
xcm 
2L
3
 Exemplo 20 – Determine o centro de massa do
sistema da figura: um triângulo de massa M.

Solução:
m1  x1  m2  x2  m3  x3
 xcm  0.75m
m1  m2  m3
m  y  m2  y2  m3  y3
 1 1
 ycm  1m
m1  m2  m3
xcm 
ycm
 Exemplo 20 – Determine o centro de massa do
da vareta de densidade linear:
(a)  constante:
(b)  = α x

Solução:
Densidade superficial:
m dm
m

 dm  ydx
A dA
A
m
2m
dm 
ydx  dm 
ydx
a b
a b
2

Física 1 – Capítulo 5 – Impulso e Quantidade de movimento – Prof. Dr. Cláudio. Sérgio Sartori.
y
Equação da reta:
b
x
a
ycm 
2m b
2m
dm 
xdx  dm  2 xdx
a b a
a
1
xcm   xdm
m
a
a
1
2m
2m
xcm   x 2 xdx  xcm 
x 2 dx
m0 a
m  a 2 0
2 x3
xcm  2
a 3
Analogamente:
x a
 xcm 
x 0
2
a
3
1u  d  sen52.5  1u   d  sen52.5   161u  0
1u  1u  16u
ycm  0m
 Exemplo 22- Jaime está a uma distância de 20
m de Rui e ambos estão em pé sobre a superfície lisa de
um lago congelado. Rui possui massa de 60.0 kg e
Jaime 90.0 kg. Na metade da distância entre os dois
homens, uma caneca contendo a bebida favorita deles
está apoiada sobre o gelo. Eles puxam a extremidade de
uma corda leve esticada entre eles. Quando Jaime se
desloca 6 m no sentido da caneca, e, que sentido Rui se
desloca e qual é a distância percorrida por ele?
1
ycm  a
3
 Exemplo 21 – Centro de massa da molécula
de água. A figura mostra a estrutura simplificada da
molécula de água.
 Solução: A superfície gelada é horizontal e
sem atrito, é nula a força externa resultante que atua
sobre Rui. O momento linear total do sistema
permanece constante.
Centro de massa:
A distância d entre os átomos é dada por:
11
d  9.57 10 m . Cada átomo de hidrogênio possui
massa igual a 1u e o átomo de oxigênio16 u.
1u  1.6605402 1027 kg
: unidade de massa
atômica. Representamos as massas por meio de pontos
porque quase toda a massa do átomo está concentrada
em seu núcleo, cujo raio é 10-5 menor do que o raio do
átomo. Usando o sistema de coordenadas indicado,
calcule a posição do centro de massa da molécula de
água.

xcm 
Solução:
xcm 
90   10   60 10
90  60
 xcm  2m
Quando Jaime se desloca 6.0 m para a caneca,
sua nova coordenada é x = -4 m. Sendo xR a
coordenada de Rui:
xcm 
90   4   60  xR
90  60
 2m  xR  1m
Jaime se deslocou 6 m no sentido da caneca e
ainda está a uma distância de 4 m da caneca; Rui se
deslocou 9.0 m e está a uma distância 1.0 m da
caneca. A razão entre as duas distâncias percorridas
é 2/3, igual à razão inversa entre suas massas.
1u  d  cos52.5  1u  d  cos52.5  161u  0
 Exemplo 22 - Propulsão de um foguete. Um
foguete está no espaço sideral, longe de qualquer
1u  1u  16u
xcm  0.068d  xcm  0.068  9.57 10
xcm  6.5 1012 m
11
planeta, quando então seu motor é acionado. Na
primeira etapa da queima, o foguete ejeta 1/120 de sua
massa com uma velocidade relativa igual a 2400 m/s.
Qual é a aceleração inicial do foguete?
11
Física 1 – Capítulo 5 – Impulso e Quantidade de movimento – Prof. Dr. Cláudio. Sérgio Sartori.
0  m  dv  dm

dv  dm  vex

0
m  dv  dm  vex
Dividindo ambos os lador por dt:
m
O termo
 Solução:
O componente x do momento do foguete no
instante inicial é:
vcomb  v   vex   vcomb  v  vex
O componente x do momento linear da massa
ejetada (-dm) é:
 dm  vcomb   dm   v  vex 
Conforme indicado na figura, no final do
intervalo dt, o componente x da velocidade do foguete
com o combustível ainda não queimado é v + dv, e sua
massa diminui para m + dm (lembre-se que dm < 0). O
momento linear do foguete nesse instante é:
 m  dm   v  dv 
dv
éa aceleração do foguete de modo
dt
que o termo esquerdo fornece a força resultante ou a
força de propulsão do foguete:
dv
dm
m   F  vex 
dt
dt
P1  m  v
Em um curto intervalo de tempo dt, a massa do
foguete varia de uma quantidade dm. Essa quantidade é
negativa, pois a massa do figuete diminui com o tempo.
Logo, no intervalo de tempo dt, uma quantidade de
massa positiva –dm resultante da combustão é ejetada
do foguete. Seja vex a velocidade escalar do material
expelido em relação ao foguete; o combustível
queimado é ejetado em um sentido oposto ao do
movimento, portanto o componente x do vetor
velocidade em relação ao foguete é – vex. O componente
x da velocidade do combustível queimado vcomb em
relação ao nosso sistema de coordenadas é:
dv
dm
 vex 
dt
dt
A força de propulsão é proporcional à
velocidade relativa vex do combustível queimado e à
taxa da variação de massa com o tempo do material
ejetado,

dm
dt
(Lembre-se que dm/dt é uma
quantidade negativa porque representa a taxa de
variação da massa do foguete. O componente x da
aceleração do foguete é:
a
dv vex dm


dt
m dt
Essa relação é positiva pois vex é positiva
(lembre-se de que ela é o módulo da velocidade de
exaustão) e dm/dt é negativa. A massa m do foguete
diminui continuamente à medida que o combustível é
consumido. Quando vex e dm/dt permanecem constantes,
a aceleração cresce até que toda a massa do combustível
seja consumida.
Um foguete de verdade queima combustível
com uma taxa muito elevada. E ejeta o combustível
queimado com uma velocidade relativa muito elevada,
como na figura abaixo.
Logo, o componente x do momento linear total
P2 do foguete mais o momento linear do combustível
queimado no instante t + dt é:
P2   m  dm    v  dv    dm    v  vex 
De acordo com a hipótese inicial, o foguete e o
combustível constituem um sistema isolado. Portanto,
existe conservação do momento linear, e o componente
x do momento linear do sistema deve ser o mesmo tanto
no instante t quanto no instante t+dt: P1 = P2. Portanto:
m  v   m  dm    v  dv    dm    v  vex 
m  v  m  v  m  dv  dm  v  dm  dv  dm  v  dm  vex
Podemos desprezar o termo dm.dv por se tratar
de duas infinitesimais. Assim:
A taxa inicial da variação da massa é:
m 120
m
dm
 0
 0
dt
1s
120
m0: massa inicial em t = 0 do foguete.
12
Física 1 – Capítulo 5 – Impulso e Quantidade de movimento – Prof. Dr. Cláudio. Sérgio Sartori.
vex dm

m0 dt
2400 m0
a

m0 120
a
a  20 m s 2
 Exemplo 23 - Velocidade de um foguete.
Suponha que ¾ da massa inicial m0 do foguete do
exemplo anterior seja de combustível, de modo que sua
massa final é m = m0/4 e imagine que o combustível
seja consumido com uma taxa constante em um
intervalo de tempo total t = 90 s. Se o foguete parte do
repouso em nosso sistema de coordenadas, calcule sua
velocidade nesse instante final.
 Solução:
m  dv  dm  vex
dm
dv  vex 
m
v
m
dm
v dv  vex  m m
0
0
m
m 
v  v0  vex  ln    vex  ln  0 
m
 m0 
m 
v  v0  vex  ln  0 
m
m
4
v  0  2400  ln    v  3327
s
1
 Texto: O neutrino. (Adaptado de 3.)
Neutrino é uma partícula sub-atômica dificilmente
detectada porque sua interação com a matéria é muito
fraca, sua carga é neutra e sua massa extremamente
pequena. A sua formação se dá em diversos processos
de desintegração em que sofre transição para um estado
de energia mais baixa, como quando o hidrogênio é
convertido em hélio no interior do Sol. Neste momento
são gerados todos os comprimentos de ondas. Wolfgang
Pauli em torno da década de trinta, observou que em vez
de ter uma energia de 0,8 MeV, o elétron quando
acelerado (emitido), possui uma energia variável entre 0
e 0,8 MeV.
Considerada uma anomalia, o cientista
procurou uma forma de adequar matematicamente a
prática e a teoria, pois ambas não eram concordantes.
Em torno de 1931, Pauli encontrou vestígios do
que poderia vir a ser outra partícula muito pequena que
acompanhava o elétron em sua aceleração. Esta foi
denominada de “neutrino”.
Somente em 1956, é que se comprovou a
existência real do neutrino, pois sua interação era tão
pequena que quase não foi possível sua detecção.
Fisicamente, o primeiro detector de neutrinos consistia
de uma cubo com 400.000 litros de tetracloroetileno.
No início da década de sessenta, foi descoberto em
laboratório que os prótons e nêutrons compunham-se de
partículas que foram chamadas de quarks.
Em meados da década de oitenta, os quarks,
juntamente com outra classe de partículas subatômicas
conhecidas como léptons, constituíam os blocos
construtores fundamentais de toda matéria.
O neutrino é uma das partículas elementares da
matéria/energia (neste caso há que se ter cuidado em
dissociar a matéria da energia). Tem o mesmo momento
angular intrínseco, spin ou giro da mesma forma que os
prótons, elétrons e nêutrons, e diferente dos fótons que
têm o dobro do giro ou spin.
Pertence à família dos léptons, sua massa é
muito pequena (antigamente se pensava que podia ser
nula). O spin do neutrino é 1/2, sua carga elétrica pode
ser considerada nula. Esta partícula é formada em
diversos processos de desintegração beta, e na
desintegração dos mésons K. Pode-se dizer (por
enquanto) que existem três tipos de neutrino. Estão
intimamente associados ao elétron, ao tau e ao múon.
 Tipos de neutrinos

Neutrino do elétron = Neutrino eletrônico é
associado ao elétron, de número eletrônico +1; neutrino
do elétron, seu símbolo é: νe

Neutrino do múon = Neutrino muônico
associado ao múon-menos, e de número muônico +1,
seu símbolo é νμ

Neutrino do tau = Neutrino tauônico,
associado ao tau, e de número tauônico +1, seu símbolo
é ν τ.
A lei da conservação do momento linear e a lei da
conservação da energia, vitalmente importantes em
todas as áreas da física, são sustentadas por uma sólida
base de evidências experimentais. Contudo, o
decaimento de núcleos radioativos por um processo
conhecido como decaimento beta levou em 1930 o
grande físico Niels Bohr a sugerir que essas leis
poderiam não ser obedecidas em processos nucleares.
Quase todos os físicos discordaram dessa hipótese,
eles acreditavam tão fortemente nessas leis de
conservação que aceitaram uma hipótese alternativa,
formulada por Wolfgang Pauli, segundo a qual uma
partícula "misteriosa" ainda não detectada deveria ser
emitida no decaimento beta. Somente 25 anos depois,
esta partícula, o neutrino. foi realmente observada
experimentalmente.
Para entendermos como surgiu esse desafio para as
leis de conservação, vamos considerar um sistema
constituído por duas partículas, com massas m1 e m2
13
Física 1 – Capítulo 5 – Impulso e Quantidade de movimento – Prof. Dr. Cláudio. Sérgio Sartori.
inicialmente em repouso. O sistema poderia ser a bala e
o rifle do exemplo discutido, ou duas bolas amarradas a
uma mola comprimida entre elas, ou um núcleo instável
que se divide em dois fragmentos. Quando os dois
corpos se separam, adquirindo velocidades v1 e v2 uma
quantidade total de energia Q é subdividida entre eles:
Q  K1  K 2 
1
1
m1  v12  m2  v22
2
2
Naquele Exemplo o valor de Q era de 225.1.
Notamos naquele exemplo que a razão entre as energias
cinéticas das partículas era inversamente proporcional à
razão entre suas massas. Para uma razão entre as massas
igual a 600:l. o rifle recuando e a bala adquiriram
energias cinéticas de (1/601)Q e (600/601)Q,
respectivamente. A energia é sempre repartida dessa
forma, ou seja. a partícula com menor massa possui uma
energia cinética maior do que a energia cinética da
partícula mais pesada.
Para provar isso, notamos que o sistema é
isolado, de modo que o momento linear total é zero
antes e depois de as partículas se separarem. Logo, o
momento linear de uma partícula é igual e contrario ao
momento linear de outra partícula:
m1  v1  m2  v2
Elevando-se ao quadrado e dividindo-se por 2
temos:
1
1
m1  v12  m2  v22
2
2
m1  K1  m2  K2
Assim, podemos relacionar com a equação que
dá o valor de Q:
K1 
m2
m1
 Q  K2 
Q
m1  m2
m1  m2
O ponto essencial é que. quando existem duas
partículas no final do processo, a energia total Q deve
sempre ser dividida dessa maneira. Quando existem três
ou mais partículas, a energia pode ser dividida de
diversas formas, dependendo da direção e do sentido do
movimento das partículas.
 Antineutrino
Além dos neutrinos existem os antineutrinos,
estes são antipartículas de neutrino. Há três tipos de
antineutrinos, um associado ao elétron, um ao múon e
um ao tau.
 Interações
Os neutrinos sofrem, apenas, interações fracas
e gravíticas. Experiências executadas em laboratórios de
partículas indicam que se transformam de um tipo em
outro durante seu deslocamento. A isto se chama
oscilações de neutrinos. Pontecorvo e outros
especularam que os neutrinos poderiam ter tais
oscilações, pois a quantidade de neutrinos medida que
chegavam à terra vindos dos Sol eram menores que o
predito pela teoria,[2] mas estas oscilações não eram
preditas no Modelo Padrão que descreve as interações
das partículas elementares. Este foi a primeira evidência
de um fenômeno não descrito pela teoria, e por isto
Koshiba e Davis ganharam um Prêmio Nobel em 2002.
A primeira observação direta deste fenómeno foi feita
pelo experimento "Opera" (Oscillation Project with
Emulsion-tRacking Apparatus) usando os dados do
CERN através de feixes de neutrinos do tipo múon
enviados do CERN ao Laboratori Nazionali del Gran
Sasso nos quais foram encontrados neutrinos tau (antes
disso, apenas o desaparecimento dos neutrinos múon foi
observado em laboratório). [2]
 Matéria transparente
Para a passagem dos neutrinos, a matéria é
transparente, isto quer dizer que atravessam a Terra (e
presume-se o Sol) praticamente sem perder energia.
Além disto, presume-se também que apenas uma
pequena fração das partículas é detida pela matéria
ordinária.
Para se ter uma idéia da transparência da matéria,
suponha-se que houvesse um detector de neutrinos e
fótons cuja passagem fosse medida quando provindos
do Sol e o aparelho hipotético os deixasse passar, ou
seja, apenas contasse a quantidade de ambos. Os fótons
após contados seriam detidos pela Terra, os neutrinos
não. Quer dizer, ao virar o instrumento para a o chão
durante a noite, e posicionando-o enxergando o Sol
através da Terra, seriam contados quase em sua
totalidade os neutrinos solares, muito poucos seriam
detidos, o planeta é transparente.
 Astrofísica e Astronomia
Em astrofísica, sabe-se que a detecção de
neutrinos é importante para se levantar os meios de
observação direta das reações termonucleares no interior
do Sol. Estes corpúsculos são testemunhas diretas da
evolução de nossa estrela. A densidade de energia em
forma de neutrinos na radiação cósmica poderá fornecer
muitas respostas acerca de nosso universo. A principal é
sobre a idade do universo e a quantidade de
matéria/energia negra presente no espaço, com estes
dados, pode-se determinar futuramente se o modelo
universal é aberto, fechado ou plano. A forma como
ocorreu o Big-Bang, a forma do tecido universal e suas
distorções, entre outras descobertas que ainda virão.
A maioria dos neutrinos que atravessam a Terra
são provenientes do Sol, e mais de 50 trilhões deles
passam através do seu corpo a cada segundo[1].
 Raios Cósmicos são partículas extremamente
penetrantes, dotadas de alta energia, que se deslocam a
velocidades próximas a da luz no espaço sideral.
Portanto, ―raios‖ cósmicos não são raios, mas partículas
de átomos.
Essas partículas ao penetrarem na Terra, colidirem com
os núcleos dos átomos da atmosfera, cerca de 10 mil
14
Física 1 – Capítulo 5 – Impulso e Quantidade de movimento – Prof. Dr. Cláudio. Sérgio Sartori.
metros acima da superfície do planeta, e dão origem a
outras partículas, formando uma ―chuva‖ de partículas
com menos energia, os chamados ―raios‖ cósmicos
secundários.
O número de partículas que chegam ao nível do
mar, em média, é de uma partícula por segundo em cada
centímetro quadrado.
Os raios cósmicos secundários são inofensivos
à vida na Terra, mas os raios cósmicos primários são
perigosos para os astronautas no espaço.
 Referências:
1.
↑ MIT News Office, "Experiment confirms
famous physics model" April 18, 2007
2.
↑ a b Particle Chameleon Caught in the act
of Changing. CERN Press Office (31 de maio de 2010).
Página visitada em 31 de maio de 2010.
3. http://pt.wikipedia.org/wiki/Neutrino, acessado
em 11/06/2010.
 Exemplo 24 - Energia em um decaimento
radioativo O isólopo radioativo 222Rn, o gás inerte
radônio, está presente no ar atmosférico. Ele sofre um
processo chamado decaimento alfa, cujos produtos
finais são um núcleo de 218Po (massa = 3.62.10-25 kg) e
uma partícula alfa (massa = 6.65.10-27kg). Essa
cãoiação, juntamente com a produzida por decaimento
posteriores, é responsável pelos riscos à saúde
provocados pelo radônio. Q quantidade de energia
liberada no decaimento do 222Rn é Q = 9.0.10-13J.
Calcule a energia cinética da partícula alfa emitida e a
energia cinética do núcleo 218Po que recua.
 Solução:
Seja m1 a massa da partícula alfa e m2 a massa
do núcleo 218Po. Podemos utilizar as equações:
K1 
m2
3.62 1025
 Q  K1 
 9.0 1013
m1  m2
3.69 1025
K1  8.8 1013 J
A energia cinética que sobra para o núcleo
218
Po é:
K2  Q  K1  2.0 1014 J
Cerca de 98 % da energia liberada é transferida
para a partícula alfa, sobrando apenas 2 % para a
energia cinética do núcleo 218Po.
Determinações experimentais do decaimento
222
Rn fornecem dados sobre o número de partículas alfa
emitidas com varias energias cinéticas (veja Figura
abaixo). Esse gráfico mostra que toda partícula alfa
emitida para cada núcleo de 222Rn em repouso possui a
mesma energia cinética, dentro da precisão do erro
experimental.
(Essas
partículas
alia
são
monoenergéticas.)
15
Se existirem somente duas partículas finais,
esse resultado é o esperado. Se todos os núcleos 222Rn
forem idênticos, então Q possuirá o mesmo valor para
todos, e K devera ser o mesmo. Portanto essa medidas
confirmam o modelo de duas partículas para o processo
de decaimento. Outro tipo de processo de decaimento
radioativo. denominado decaimento beta, envolve um
elétron e sua antipartícula, o pósitron. O elétron algumas
vezes é chamado de partícula beta negativa ( -) e o
pósitron algumas vezes é chamado de partícula beta
positiva ( +). Um exemplo de decaimento  - ocorre
com o núcleo instável 210Bi, que, emitindo um elétron,
decai para o núcleo 210Po. Suponha que esse evento seja
um decaimento envolvendo duaspartículas, como no
caso da emissão da partícula alia. A massa de repouso
do núcleo 210Po é 383000 vezes maior do que a massa
de repouso do elétron: um calculo semelhante ao
realizado no Exemplo anterior prevê que virtualmente
toda a energia libertada Q = 1.86.10-13 J deve ir para o
elétron e que os elétrons provenientes de todos os
decaimentos são monoenergéticos. (Os cálculos exigem
o uso de expressões relativísticas para a energia cinética
e para o momento linear do elétron, desenvolvidas no
Volume 4, porque um elétron emitido em um
decaimento beta se move com uma velocidade que
chega até 95% da velocidade da luz.)
Henri
Becquerel,
que
descobriu
a
radioalividade em 1896. encontrou por volta do ano
1900 indícios de que os elétrons emitidos em processos
de decaimento  - não eram monoenergéticos.
Medidas realizadas por J ames Chadwick, o
descobridor do nêutron, sugeriram mais fortemente essa
hipótese. No caso do decaimento do 210Bi, experiências
posteriores indicaram um intervalo de energias para o
elétron, com um valor máximo igual a 1.86.10-13J
(Figura acima, à direita). Como a lei da conservação do
momento linear e a lei da conservação da energia
previam que todos os elétrons deveriam ter a mesma
energia, estes resultados levantaram dúvidas sobre a
validade destas leis.
Procurando um modo de salvar as leis de
conservação, em 1931 Woltgang Pauli sugeriu a
existência de uma terceira partícula eletricamente neutra
Física 1 – Capítulo 5 – Impulso e Quantidade de movimento – Prof. Dr. Cláudio. Sérgio Sartori.
que deveria ser emitida durante o decaimento  -. Caso
ela existisse, poderia contribuir com alguma energia e
algum momento linear.
Os momentos lineares e as energias de três
partículas podem ser divididos de muitos modos
diferentes de acordo com as leis de conservação. Com
duas partículas (Figura abaixo (a)), os momentos
lineares devem ser iguais e opostos, e esta condição
exige que as energias das partículas não sejam iguais.
Porém com três partículas, o momento linear igual a
zero implica um triângulo que representa a soma
vetorial dos momentos lineares (Figuras b, c, d),
permitindo que os momentos lineares e as energias das
três partículas possam ser divididos de muitos modos,
desde que a soma das energias seja igual a Q. Sendo
assim, com a hipótese da existência de uma terceira
partícula, o elélron poderia possuir um intervalo
completo de energias desde zero até um máximo quase
igual a Q conforme observado.
Quando Pauli sugeriu a existência dessa
partícula neutra, o físico italiano Enrico Fermi
inicialmente havia chamado essa partícula de nêutron.
porém Chadwick já havia usado este nome para uma
outra partícula neutra com massa elevada. Então Fermi
batizou-a de neutrino (um nêutron pequeno). (Na
nomenclatura atual, a partícula emitida no decaimento
 - denomina-se antineutrino, que e a antipartícula do
neutrino.) Medidas posteriores das energias dos eltrons
no decaimento  - revelaram coerência com a
possibilidade de existência dessa partícula neutra
invisível. Como sua interação com outras partículas c
extremamente fraca, e muito difícil detectá-la. Somente
em 1956 é que os neutrinos foram detectados
diretamente. Porem, no intervalo de tempo até sua
descoberta, os físicos confiavam tanto nas leis de conservação que ninguém duvidava de que ele seria
encontrado.
A importância do neutrino na física moderna
vai muito além de auxiliar a confirmação de leis de
conservação. Os neutrinos auxiliam nossa compreensão
do que ocorre em uma supernova, um dos fenômenos
mais dramáticos da natureza, no qual uma estrela que
possui massa muitas vezes maior do que a massa do Sol
explode espetacularmente. A supernova próxima mais
recente, a SN 1987A, foi observada no dia 24 de
fevereiro de 1987 (Figura a seguir). No mesmo instante,
dois laboratórios na Terra (um no Japão e outro
embaixo do lago Erie) detectaram um total de 19
neutrinos provenienles da direção da SN 1987A. Como
as interaçóes dos neutrinos são extremamente fracas, até
mesmo detectar esse número grande de neutrinos exigiu
o uso de enormes delelores que usavam milhóes de
quilogramas de água pura. (As colisões de neutrinos
com os núcleos dos átomos de agua produzem partículas
secundárias que se deslocam com velocidades elevadas,
que por sua vêz produzem breves emissões de luz. São
esses flashes de luz que são detectados.) A análise dos
dados mostrou que durante o primeiro segundo da
explosão da supernova, aproximadamente 1058 neutrinos
foram emitidos da supernova. com uma energia total de
1046J - cerca de 100 vezes mais energia do que a emitida
pelo Sol nos últimos cinco bilhões de anos!
(Aproximadamente 5.1014 neutrinos provenientes dessa
supernova atravessaram o seu corpo naquela segundafeira de 1987; a probabilidade de que apenas um desses
neutrinos interagisse com o seu corpo seria de apenas
cerca de l em 5000, embora essa interação não pudesse
produzir nenhum efeito biológico sobre você.) Esses
neutrinos foram produzidos por reações nucleares nas
profundezas do núcleo da supernova; a detecção de
apenas 19 neutrinos foi suficiente para fornecer aos
astrofísicos informações direlas sobre essas reações.
Fotografia da Supernova 1987ª antes (lado esquerdo) e
depois (lado direito) da explosão. Menos de 0.1% da energia libertada
pela supernova foi convertida em luz visível; a maior parte da energia
restante foi fornecida para os nentrinos.
Instigada pela observação da SN 1987A, uma
nova geração de "telescópios de neutrinos" está
entrando em operação. O maior de todos é o DUM
ANO (iniciais de Deep Underwater Muon and Neutrino
Detector, que significa detector de neutrino e múon
embaixo de águas profundas), o qual procura detectar
flashes produzidos por neutrinos que passam através da
camada de 4800 m de água limpa no Oceano Pacífico
longe das Ilhas do Havaí. Varrendo minuciosamente 108
toneladas de água do mar, o DUMAND procura
neutrinos com energias ultra-elevadas que, segundo as
previsões, seriam emitidos pela matéria que cai em um
buraco negro de massa muito elevada. A física dos
neutrinos continua a ser um campo de pesquisas vital e
excitante.
16
Física 1 – Capítulo 5 – Impulso e Quantidade de movimento – Prof. Dr. Cláudio. Sérgio Sartori.
Equilíbrio de um corpo rígido.
Pressão de uma força.
Para um corpo em equilíbrio estático, devemos
ter soma das resultantes nula e soma dos momentos em
relação a um ponto também nulo:
 

F
  i  0
i
N 

 M io  0
 i
N

Pressão:
Definimos como a razão entre a força e a área
na qual a força está aplicada:
P = F/A
 Unidade: SI: 1Pa = 1N/m2 (Pascal)
Unidades importantes:
1 atm = 105Pa – 760 mm Hg
Lei da Gravitação Universal:
A grande galáxia M31 na constelação de
Andrômeda possui uma extensão maior do que 10 18 km
(100 000 anos-luz). Sua distância até a Terra é igual a
aproximadamente 2,9 x 106 anos-luz. Todos os corpos
desta galáxia — estrelas, gases luminosos, poeira
interestelar e outros materiais não visíveis nesta imagem
— são mantidos em órbita em torno do centro de massa
da galáxia pela ação da mútua atração gravitacional
existente entre eles.
Por que os planetas, as luas e o Sol são
aproximadamente esféricos? Por que alguns satélites
artificiais da Terra giram em tomo dela em 90 minutos
enquanto a Lua leva 27 dias para completar uma volta
em tomo da Terra? E por que os satélites não caem e
retomam para a Terra? O estudo da interação gravitacional oferece respostas para estas e outras
perguntas relacionadas.
Conforme acentuamos, a gravitação é uma das
quatro classes de interações existentes na Natureza, e
ela foi a primeira das quatro a ser estudada
extensivamente. No século XVII, Newton descobriu que
a interação que mantém os planetas em órbita ao redor
do Sol é a mesma que faz a maçã cair de uma macieira.
Isso marcou o começo da mecânica celeste, o estudo da
dinâmica dos astros. Hoje, nosso conhecimento da
mecânica celeste nos permite determinar como colocar
um satélite artificial da Terra em uma órbita desejada ou
escolher a trajetória exata para enviar uma nave espacial
para outro planeta.
Estudaremos as leis básicas que governam a
interação gravitacional. Esta lei é universal: a gravidade
atua do mesmo modo entre a Terra e o seu corpo, entre
o Sol e um planeta, e entre um planeta e uma das suas
luas. Aplicaremos a lei da gravitação para fenômenos
tais como a variação do peso com a altura, as órbitas de
um satélite em torno da Terra e as órbitas de planetas
em tomo do Sol.
LEI de NEWTON da
grAVITAÇÃO
O seu peso, a força que atrai você para o centro da
Terra, talvez seja o mais familiar exemplo de atração
gravitacional que você conhece. Estudando o
movimento da Lua e dos planetas, Newton descobriu o
caráter fundamental da atração gravitacional entre dois
corpos de qualquer natureza. Juntamente com as três
leis do movimento, Newton publicou a lei da
gravitação em 1687. Ela pode ser enunciada do seguinte modo:
Cada partícula do universo atrai qualquer outra
partícula com uma força diretamente proporcional ao
produto das respectivas massas e inversamente
proporcional ao quadrado da distância entre as
partículas.
Traduzindo matematicamente, essa lei pode ser
escrita na forma:
F12 
Gm1 m2
r 212
(lei da gravitação), onde F12 é o módulo da força
gravitacional que atua sobre cada partícula, m1 e m2 são
as massas das partículas, r12 é a distância entre elas e G
é uma constante física fundamental denominada
constante gravitacional. O valor numérico de G
depende do sistema de unidades usado.
G = 6,67 10-11 N m2/kg2
ATENÇÃO: Como os símbolos g e G são
muito parecidos, é muito comum confundir as grandezas
gravitacionais representadas por estes símbolos. A letra
minúscula g é a aceleração da gravidade, que relaciona
o peso w com a massa m do corpo através da equação w
= mg. O valor de g é diferente em locais diferentes da
Terra e sobre as superfícies de outros planetas. Em
contraste, a letra maiúscula G relaciona a força entre
dois corpos com as suas massas e a distância entre eles.
A constante G denomina-se universal porque ela possui
sempre o mesmo valor para dois corpos
independentemente dos locais do universo onde os
corpos estejam.
Leis de Kepler:

O MOVIMENTO DE PLANETAS
A palavra planeta deriva de um termo grego que
significa "errante", e na verdade os planetas mudam
constantemente de posição no céu em relação ao fundo
17
Física 1 – Capítulo 5 – Impulso e Quantidade de movimento – Prof. Dr. Cláudio. Sérgio Sartori.
das estrelas. Um dos maiores êxitos intelectuais dos
séculos XVI e XVII foi a verificação de três fatos: a
Terra também é um planeta, todos os planetas
descrevem órbitas em tomo do Sol e todos os movimentos aparentes dos planetas vistos da Terra podem ser
usados para uma determinação precisa de suas órbitas.
Nicolau Copémico publicou em 1543 na
Polônia a primeira e a segunda conclusão acima
mencionadas. A determinação das órbitas dos planetas
foi realizada entre 1601 e 1619 pelo astrônomo e
matemático alemão Johannes Kepler, usando um
conjunto volumoso de dados precisos sobre os
movimentos aparentes compilados pelo seu preceptor, o
astrônomo dinamarquês Tycho Brahe. Por meio do
método das tentativas, Kepler descobriu três leis
empíricas que descrevem com acurácia o movimento
dos planetas:
1. Cada planeta se move em uma órbita elíptica tal
que o Sol ocupa um dos focos da elipse.
2. A linha que liga o Sol a um planeta varre áreas
iguais a intervalos de tempo iguais.
3. O período ao quadrado de um planeta é
proporcional ao cubo do comprimento do eixo maior
da elipse descrita pelo respectivo planeta.
T12 T22

k
a13 a 23
Kepler não sabia por que os planetas se moviam
desse modo. Três gerações mais tarde, quando Newton
estudava o movimento dos planetas, ele descobriu que
cada uma das leis de Kepler poderia ser deduzida; elas
decorrem das leis do movimento de Newton e da lei da
gravitação. Vamos examinar separadamente cada uma
das leis de Kepler e verificar como surge cada uma
delas.
Inicialmente vamos considerar a órbita elíptica
mencionada na primeira lei de Kepler. A Figura mostra
a geometria de uma elipse. A dimensão maior
corresponde ao eixo maior, ea é a metade do
comprimento do eixo maior; este comprimento é o
semi-eixo maior. A soma das distâncias de S até P e de
S' ale P é a mesma para todos os pontos sobre a curva.
Os pontos S e S ' são os focos. O Sol está no ponto S e o
planeta está no ponto P; consideremos estes astros como
pontos, porque suas dimensões são muito menores do
que a distância entre eles. Não existe nada no outro foco
S'.
A distância de cada foco até o centro da elipse é
igual a ea, onde e é um número sem dimensões entre 0 e
l denominado excentricidade. Quando e = 0, a elipse é
uma circunferência. As órbitas reais dos planetas são
aproximadamente circulares; suas excentricidades
variam de 0,007 para Vênus a 0,248 para Plutão (a
excentricidade da Terra é e = 0.017). O periéiio
corresponde ao ponto mais próximo do Sol na órbita do
planeta e o afélio corresponde ao ponto mais afastado
do Sol na órbita do planeta.
Newton foi capaz de verificar que, quando uma
força proporcional a 1/r2; atua sobre um corpo, as únicas
órbitas fechadas possíveis são a elipse e a
circunferência; ele também mostrou que órbitas abertas
devem ser parábolas ou hipérboles. Estes resultados
podem ser obtidos de forma direta usando-se as leis do
movimento de Newton e a lei da gravitação, juntamente
com algumas equações diferenciais que você ainda não
está preparado para resolver.
A segunda lei de Kepler é indicada na Figura
anterior. Em um pequeno intervalo de tempo dt a linha
que liga o Sol ao planeta descreve um ângulo dθ. A área
varrida é dada pelo triângulo sombreado de altura r,
18
Física 1 – Capítulo 5 – Impulso e Quantidade de movimento – Prof. Dr. Cláudio. Sérgio Sartori.
base r dθ e área dA = rdrdθ. A taxa com a qual esta área
é varrida, dA/dt, denomina-se velocidade setorial:
dA
dt
 12 r 2
d
dt
A essência da segunda lei de Kepler consiste em
dizer que a velocidade setorial permanece constante
qualquer que seja o ponto da órbita. Quando o planeta
está próximo do Sol r é pequeno e dθ/dt possui valor
grande; quando o planeta está longe do Sol r é grande e
dθ/dt possui valor pequeno.
Programa para Astronomia: download:
19
www.shatters.net/celestia
TRABALHO – OPTATIVO:
1. Com o auxílio do programa, dê as
características principais de todos os astros disponíveis
no sistema solar.
Tente reproduzir as seguintes situações:
2. Usando o Software Interactive Physics, (faça
um download em
www.interactivephysics.com/demo.html
Construa um sistema massa mola, com massa
de 2 kg e constante elástica da mola de 200N/m; variar a
constante da mola até que seja possível visualizar a
animação e construir os gráficos velocidade versus
Física 1 – Capítulo 5 – Impulso e Quantidade de movimento – Prof. Dr. Cláudio. Sérgio Sartori.
tempo, posição e aceleração versus tempo. Indique os
vetores velocidade e aceleração.
Exemplos – Tipler – Capítulo 8
1. Localize o centro de massa da molécula de
água:
Parte
1
2

mi
8m
m
9m
xCM 

Solução:
xCM 
xCM 
xCM
m  x
i
i
m  x
i
i
i
M
 mi  yi
i
M
yiCM
0.2
0.5
mi.xiCM
3.2m
0.7m
3.9m
mi.yiCM
1.6m
0.5m
2.1m
 xCM 
3.9m
 xCM  0.433m
9m
 yCM 
2.1m
 yCM  0.233m
9m
i
M
mH  xH1  mH  xH 2  mO  xO
mH  mH  mO
5.9 pm

2 1u  9.6 pm  cos 52.2  mO  0

1u  1u  16u
xCM  0.66 pm
yCM 
yCM 
xiCM
0.4
0.7
3. Um projétil é disparado sobre um campo
horizontal, com velocidade igual a 24.5 m/s, sob um
ângulo de 36.9°. No ponto mais elevado da trajetória, o
objeto explode e se divide em dois fragmentos de
massas iguais. Umd eles cai na vertical até o solo. Em
que ponto o outro fragmento atinge o solo?
m  y
i
i
 yCM  0
M
CM   xCM , yCM    0.66nm,0 
i
2. Ache o centro de massa do compensado da
figura:

Solução:
mcm  xcm  m1  x1  m2  x2
2m  R  m  0.5R  m  x2  x2  1.5R
v02
24.52
R  sen  2   R 
sen  73.8 
g
9.81
R  58.8m
x2  1.5R  x2  88.2m
 Solução:
Dividindo a folha em duas partes:
20
Física 1 – Capítulo 5 – Impulso e Quantidade de movimento – Prof. Dr. Cláudio. Sérgio Sartori.
4. Duas pessoas, uma de 80 kg e outra de 120
kg, estão num barco de massa 60 kg que flutua num
lago. A primeira está remando no centro do barco e a
outra na proa, a 2 m do centro. Depois de um certo
tempo, a segunda pessoa se oferece para remar. Com o
barco parado, as duas pessoas trocam de lugar. Nessa
troca, de quanto se desloca o barco ? (Despreze o efeito
das forças horizontais da água).
Fn  m1  g  m2  g  M  acm, y
Fn  (m1  m2 )   g  acm, y 
A componente vertical da aceleração do centro
de massa em termos da aceleração do bloco é:
M  acm, y  m1  a1, y  m2  a2, y

0
m1
 a1, y
m1  m2
 a1  sen  a1, y   g  sen  sen
acm, y 
a1, y
a1, y   g  sen2


m1
Fn  (m1  m2 )   g 
   g  sen 2  
m1  m2


2
Fn  (m1  m2 )  g  m1  g  sen 

xCM 
 
xCM
Solução:
Cálculo da coordenada x do centro de massa:
m  x
i
i
M
 mi  xi
i
i
 xCM 
80  0  60  0  120  2
 xCM  0.923m
80  60  120
120  0  60  0  80  2
 
  0.615m
 xCM
 xCM
M
80  60  120
  0.923  0.615  x  0.308m
x  xCM  xCM
6. Durante um reparo no telescópio espacial
Hubble, um astronauta substitui dois painéis solares
cujas molduras estão deformadas. Ao lançar o painel
defeituoso no espaço, o astronauta é impelido na direção
oposta. Imaginemos que a massa do astronauta seja de
60 kg e do painel 80 kg. Em relação à nave espacial, o
astronauta está em repouso no instante que arremessa o
painel, A velocidade deste, em relação à nave, é de 0.3
m/s. Qual a velocidade do astronauta em relação à nave,
depois do arremesso do painel ? ( Nessa operação, o
astronauta está ligado à nave por um cabo. Vamos
admitir que este cabo não sofra esforços durante o
processo.)
5. Um prisma triangular de massa m2 está
montado numa balança de molas. Um pequeno bloco de
massa m escorrega sem atrito sobre a face inclinada do
prisma. Determinar a leitura da balança durante o
escorregamento do bloco.

Solução:
A componente vertical das forças, pela 2ª lei
de Newton, leva a determinação de Fn:

Solução

 
p p  pa  0
21
Física 1 – Capítulo 5 – Impulso e Quantidade de movimento – Prof. Dr. Cláudio. Sérgio Sartori.
m p  v p  ma  va  0  va  
mp
ma
80
m
va    0.3  va  0.4
60
s
 vp

Solução:
7.
Um vagão aberto, de 14000kg, está
rolando a 4 m/s sobre os trilhos. Uma chuvarada súbita
enche o vagão de 2000 kg. Depois da chuvarada, quanto
tempo leva o vagão para cobrir a distância de 500 m
sobre os trilhos? Admita que a chuva caia verticalmente
e que seja desprezível o alentecimento do vagão pelo
atrito.
22
A velocidade final vf e o momento final pf estão
relacionados por:
pf  mvf
A conservação do momento permite relacionar
o momento final ao momento inicial:
pi  p f

Solução:
Tempo entre o final da chuvarada e o instante
que o vagão acaba de cobrir a distância d sobre os
trilhos:
t 
d
500
 t 
vi
vi
0  48  v1  5   v1  7 
A conservação do momento dará a relação
entre a velocidade vf final do vagão e a sua velocidade vi
antes da chuvarada:
mv  vi  mw  0   mv  mw   v f  v f 
vf 
t 
O momento inicial pi é nulo. Sejam v1 e p1 a
velocidade e o momento da garota depois do 1°
arremesso. O momento p1 é o da prancha de skate mais
o da garota e um peso: a massa dá: 40+5+3=48kg. Com
velocidade v1 mais o momento do outro peso com
velocidade v1 -7
v1 
35
m
 v1  0.66
53
s
Quando o segundo peso é arremessado, o
mv
 vi momento inicial da garota, do skate e do peso é 48.v1. A
mv  mw
conservação do momento nos dá:
14000
4
14000  2000
m
v f  3.5
s
500
 t  143s
3.5
8. Sobre um skate de 3 kg, uma garota de 40
kg segura dois pesos de 5 kg. Em repouso, a garota
arremessa os pesos, um após o outro, horizontalmente
para trás. A velocidade de cada peso em relação à garota
e ao skate é de 7.0 m/s no instante do arremesso. Que
velocidade adquire a garota na direção oposta à do
lançamento do segundo peso? Admitir ausência de
atrito.
48  v1  43  v2  5   v2  7 
v2 
48  v1  35
m
 v2  1.73
48
s
9. Um núcleo de tório 227, em repouso,
desintegra-se num outro de rádio 223 (massa 223 u)
pela emissão de uma partícula  (massa 4 u). A energia
cinética desta partícula é 6.00 MeV. Qual a energia
cinética do núcleo de rádio ao recuar?

Solução:
Física 1 – Capítulo 5 – Impulso e Quantidade de movimento – Prof. Dr. Cláudio. Sérgio Sartori.


pf  0
Conservação do momento:
m  v  mRa  vRa  vRa 
O impulso será:
m
 v
mRa
 

m
m
I  0  3.5kg.  ˆj  I  3.5kg.  ˆj
s
s
Energia cinética:
m

mRa     v 
 mRa


2
2
mRa  vRa
 EcRa
2
m m  v2
     EcRa  0.107 MeV
mRa 2
EcRa 
EcRa
2
10. Um carateca experimentado pode quebrar
um tijolo de um só golpe. Imagine que a massa da mão
e do pulso seja de 0.7 kg e a velocidade do golpe 5.0
m/s. Vamos admitir que o movimento cesse dentro de
uma distância de 6 mm do ponto de contato inicial.
(a) Que impulso o tijolo exerce sobre a mão do
carateca?
(b) Qual o tempo aproximado da colisão e qual
a força média exercida pelo tijolo?
(b) O tempo de colisão pode ser estimado
por:
t 
y
y
0.006
 t 
 t 
 t  2.4ms
1
vméd

2.5
v
2

 


I
3.5 ˆj
I  Fmed  t  Fmed 
 Fmed 
t
0.0024

Fmed  1.46(kN ) ˆj
11. Um carro, transportando um manequim
para ensaios de colisão, com 80 kg, bate em frente com
um muro a 25 m/s (90 km/h). Estimar a força que o
cinto de segurança exerce sobre o manequim durante a
colisão.


Solução:
Momento inicial do manequim:
p  m  v  2000 kgsm
Solução:
(a) O impulso é igual a variação da
quantidade de movimento:

 

I  p  p f  pi
A variação do momento é igual ao módulo do
impulso exercido pelo cinto de segurança sobre o
manequim:


I  p  2000 kgsm
Estimativa do tempo de colisão:
t 
x
1
 t 
 t  0.08s
vméd
12.5
Cálculo da força média:
I
2000
 Fmed 
t
0.08
 25000 N  Fmed  25kN
I  Fmed  t  Fmed 
Fmed
Momento inicial: mão do carateca no instante
que atinge o tijolo com a velocidade v:
m


pi  0.7  5  ˆj  pi  3.5kg.  ˆj
s
12. Uma bola de golfe recebe um golpe do taco.
Que estimativas são razoáveis para:
(a) o impulso I.
(b) o tempo de colisão t.
23
Física 1 – Capítulo 5 – Impulso e Quantidade de movimento – Prof. Dr. Cláudio. Sérgio Sartori.
(c) a força média Fmed. Uma bola de golfe
típica tem a massa m = 45 g e o raio igual a r = 2 cm.
Num golpe normal, o alcance é cerca de R = 160m.


(a) Conservação da quantidade de movimento
relacionará a velocidade final do sistema, vcm, às
velocidades iniciais:
Solução:
(a) O impulso é igual à variação da
quantidade de movimento da bola:
I  m  v0
A velocidade inicial está relacionada com o
alcance dado por:
30  4  60  0   3  60   vcm  vcm  0.19 m s
(b) A energia mecânica inicial do sistema
livro+astronauta é:
Ei 
mb  vb2
3  42
 Ei 
 Ei  24 J
2
2
v
sen20
g
Escolhendo 0  45 , que corresponde ao
A energia mecânica final é a energia cinética do
astronauta com o livro:
máximo
Ef
 sen20  1 ,
calculamos
a
velocidade inicial:
v0  R  g  v0  160  9.81  v0  40
m
s
O impulso será:
I  m  v0  I  0.045  40  I  1.8N .s
2
mb  ma   vcm


2
63  0.192
 Ef 
 E f  1.38 J
2
(c) Igualando o impulso do astronauta à variação
de seu momento, teremos:
I  past  mast  vast  60  0.19  I  11.4 N .s
14. Num ensaio de tiro, uma bala atinge o
pêndulo esquematizado na figura.
O tempo de colisão será estimado por:
x
x
0.02
t 
 t 
 t 
 t  0.001s
1
vméd
20
v0
2
A força média será:
I
1.8
 Fmed 
t
0.001
 1800 N
I  Fmed  t  Fmed 
Fmed
13. Um astronauta , de 60 kg, está numa
caminhada espacial para reparar um satélite de
comunicações. Num certo instante, precisa consultar o
manual de operações. Um outro astronauta arremessa o
livro na direção do primeiro, com velocidade de 4.0 m/s
em relação à nave espacial. Antes de pegar o livro, de 3
kg, o primeiro astronauta estava em repouso em relação
à nave. Calcular (a) a velocidade do astronauta ao
segurar o livro (b) a energia mecânica inicial e final do
sistema livro-astronauta e (c) o impulso que o livro
transmite ao astronauta.
24
mb  vb  ma  va   ma  mb   vcm
2
0
R
alcance
Solução:
O bloco do pêndulo, com a bala cravada,
oscila para cima. A altura atingida pelo bloco permite a
determinação da velocidade da bala. Sendo as massas
m1 e m2 e sendo a altura h, como se calcula a
velocidade?
 Solução:
Pela conservação da quantidade de
movimento na colisão, determina-se v1i em termos de vf:
Física 1 – Capítulo 5 – Impulso e Quantidade de movimento – Prof. Dr. Cláudio. Sérgio Sartori.
m1  v1i  m2  v2   m1  m2   v f
v1i 
m1  m2
vf
m1
Com a conservação da energia mecânica após
a colisão, determina-se vf em termos da altura:
 m1  m2   v 2f
2
  m1  m2   g  h
vf  g  h
v1i 
16.
Um bloco de 4 kg se move para a
direita com velocidade 6 m/s e colide elasticamente com
um um bloco de 2 kg movendo-se para a direita com
velocidade 3 m/s. Encontre a velocidade final dos
blocos.

m1  m2
 g h
m1
Solução:
Aplicando
movimento:
15. O ensaio do item anterior é repetido, porém
com uma caixa oca no lugar do bloco maciço. A bala
atinge a caixa e a atravessa completamente. Um
medidor a laser mostra que a bala sai da caixa com a
metade da velocidade inicial. Que altura atinge a caixa?
a
conservação
da
quantidade
de
m1  v1i  m2  v2i  m1  v1f  m2  v2 f
4  6  2  3  4  v1f  2  v2 f  4  v1f  2  v2 f  30
Aplicando a definição de choque elástico:
e
1
vrafastamento
vraproximação
e
v2 f  v1 f
v1i  v2i
v2 f  v1 f
 v2 f  v1 f  3
63
v2 f  v1 f  3


4  v1 f  2  v1 f  3  30
6  v1 f  30  6  v1 f  4

v2 f  7
Solução:
A conservação da energia mecânica relaciona
a altura h final da caixa com a velocidade v2 logo após a
colisão:
m2  v22
 m2  g  h
2
A conservação do momento relaciona a
velocidade v2 da caixa à velocidade v0:
m2  v2  m1 
m
s
m
s
17.
Um nêutron de massa mn e velocidade
vn1 colide elasticamente com um núcleo de átomo de
carbono de massa mC inicialmente em repouso.
(a) Quais são as velocidades finais de ambas as
partículas?
(b) Que fração de sua energia cinética final o
nêutron perdeu?
v0
m
 m1  v0  v2  1 v0
2
2m2
 m1

v0 

2
2m
v
h 2 h 2 
2g
2g
2
2
m v
h 1 2 0
8  m2  g
2

Solução:
Conservação do momento:
mn  vni  mn  vnf  mC  vCf
Coeficiente de restituição:
25
Física 1 – Capítulo 5 – Impulso e Quantidade de movimento – Prof. Dr. Cláudio. Sérgio Sartori.
e
18. Um pequeno carro, com massa de 1.2 Mg
(1.2.103kg), avançando para leste a 60 km/h, colide num
cruzamento com um caminhão de 3 Mg, que avança
para o norte, a 40 km/h. O carro e o caminhão
constituem um só destroço após a colisão. Determine a
velocidade dos dois logo após o desastre.
vraf
vrap
vC  vvf
e
vni
Supondo conservação da energia (choque
elástico):
e 1
vCf  vnf
 1  vni  vCf  vnf
vni
vCf  vni  vnf
mn  vni  mn  vnf  mC  vCf
mn  vni  mn  vnf  mC   vni  vnf
26

mn  vni  mn  vnf  mC  vni  mC  vnf
vnf 

Solução:
mn  mC
 vni
mn  mC
 m  mn 
vnf    C
  vni
 mn  mC 
vCf  vni  vnf

 m  mn 
 C
vni
 mn  mC 
 mn  mC    mC  mn  
vCf  
 vni
mn  mC
2mn
vCf 
 vni
mn  mC
Como a colisão é elástica, a perda de energia
cinética pelo nêutron é a energia cinética final do cúcleo
de carbono:
f 
K n KCf

K ni
K ni
1
2
mC  vCf2
mC  vCf 
2
f 
 f 


1
mn  vni 
2
mn  vni
2
m
f  C
mn
f 
 2mn 


 mn  mC 
4  mC  mn
 mn  mC 
2
2

pc

pt
Momentos antes da colisão:
km 



 mc  vc  iˆ  pc  1.2  60  iˆ  pc  72  iˆ  Mg 

h 

km 



 mt  vt  ˆj  pt  3  40  ˆj  pt  120  ˆj  Mg 

h 

Aplicando a conservação do momento:

 
pc  pt  P
1  
 


pc  pt  M  vcm  vcm    pc  pt 
M
1

vcm 
 72  iˆ  120  ˆj
4.2

 km 
vcm  17.1 iˆ  28.6  ˆj 

 h 

tg 
vcmy
vcmx
 tg 

28.6
   59
17.1
19. Encontre a velocidade final para a colisão
dos dois blocos do exemplo 16 transformando as
velocidades no referencial do centro de massa.

Solução:
Física 1 – Capítulo 5 – Impulso e Quantidade de movimento – Prof. Dr. Cláudio. Sérgio Sartori.
Calculando a velocidade do centro de massa:
m  v  m2  v2i
46  23
vcm  1 1i
 vcm 
m1  m2
42
m
vcm  5
s
Calcular: (a) a velocidade de exaustão dos
gases.
(b) o tempo de combustão tb;
(c) a aceleração inicial na partida;
(d) a aceleração no final da queima do
combustível no instante tb e
(e) a velocidade final do foguete.
Transformando as velocidades iniciais no
referencial do centro de massa, subtraindo de vcm das
velocidades iniciais:
m
s
m
u2i  v2i  vcm  u2i  3  5  u2i  2
s
27
u1i  v1i  vcm  u1i  6  5  u1i  1
Resolvendo a colisão no referencial do centro
de massa:
m
s
m
 2
s
u1 f  u1i  u1 f  1
u2 f  u2i  u2 f
Para achar as velocidades finais, adiciona-se
vcm a cada velocidade final:
m
s
m
7
s
v1 f  u1 f  vcm  v1 f  1  5  v1 f  4
v2 f  u2 f  vcm  v2 f  2  5  v2 f
20. O foguete Saturno V, usado no programa
espacial Apolo de exploração da Lua, tinha a massa
inicial de 2.86.106kg e a carga útil de 27% do total. A
taxa de combustão |dm/dt| era de 13.84.103kg/s e o
empuxo de 34.106N.

Solução:
(a) Cálculo de uex pelo empuxo e taxa de
combustão:
uex = 2.46 km/s
(b) Cálculo da massa final do foguete:
mt = 0.27m0 = 7.70.105kg
tempo de combustão: tb =(m0 – mt)/R = 150 s
(c) Cálculo de dv/dtpara m = m0 e m = mt:
Início: dv/dt = 2.14 m/s²
Final: dv/dt = 34.4 m/s²
(d) Cálculo da velocidade final: vf = 1.75 km/s
Física 1 – Capítulo 5 – Impulso e Quantidade de movimento – Prof. Dr. Cláudio. Sérgio Sartori.
28