GGM00161- 24/08/2010
Turma M2
Conjunto convexo
Definição: Um conjunto de pontos chama-se convexo
se, quaisquer que sejam dois pontos distintos desse
conjunto, o segmento que tem esses pontos por
extremidades está contido nesse conjunto.
Polígono
8 vértices
8 lados
Polígono
8 vértices
8 lados
Região Poligonal
Polígono convexo
Classificação- quanto ao número de lados
Diagonal
Perímetro
Ângulo Interno
Ângulo externo
Polígono regular
Número de Diagonais
Exemplos: n = 3 , n = 4
Considere um polígono convexo de n lados:
Qual é o número de diagonais que sai de cada
vértice?
Número de Diagonais
Exemplos: n = 3 , n = 4
Considere um polígono convexo de n lados:
Qual é o número de diagonais que sai de cada
vértice? n-3
Número de Diagonais
Exemplos: n = 3 , n = 4
Considere um polígono convexo de n lados:
Qual é o número de diagonais que sai de cada
vértice? n-3
Como cada diagonal tem extremidades em dois vértices,
Número de Diagonais
Exemplos: n = 3 , n = 4
Considere um polígono convexo de n lados:
Qual é o número de diagonais que sai de cada
vértice? n-3
Como cada diagonal tem extremidades em dois vértices,
cada diagonal foi contada duas vezes.
Número de Diagonais
Exemplos: n = 3 , n = 4
Considere um polígono convexo de n lados:
Qual é o número de diagonais que sai de cada
vértice? n-3
Como cada diagonal tem extremidades em dois vértices,
cada diagonal foi contada duas vezes. Daí
Exemplo: 1) calcule o número de diagonais de um hendecágono
ou undecágono.
Exemplo 2: Existe polígono convexo que tem 77 diagonais?
Soma dos ângulos internos
Prova:
Soma dos ângulos internos
Prova: Seja um poligono de n lados.
Soma dos ângulos internos
Prova: Seja um poligono de n lados.
Trace todas as diagonais de um vértice qualquer
(verifique no exemplo ao lado)
Soma dos ângulos internos
Prova: Seja um poligono de n lados.
Trace todas as diagonais de um vértice qualquer
(verifique no exemplo ao lado)
Considere os n – 2 triângulos formados.
Soma dos ângulos internos
Prova: Seja um poligono de n lados.
Trace todas as diagonais de um vértice qualquer
(verfique no exemplo ao lado)
Considere os n – 2 triângulos formados.
Então a soma das medidas dos ângulos internos de um polígono
Convexo é exatamente a soma dos ângulos internos desses n-2
triângulos .
Soma dos ângulos internos
Prova: Seja um poligono de n lados.
Trace todas as diagonais de um vértice qualquer
(verfique no exemplo ao lado)
Considere os n – 2 triângulos formados.
Então a soma das medidas dos ângulos internos de um polígono
Convexo é exatamente a soma dos ângulos internos desses n-2
triângulos . Portanto
Soma dos ângulos externos
Ângulos de um polígono regular
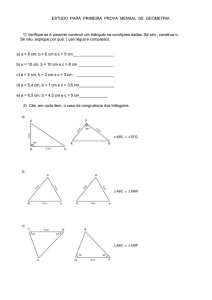
Exercício:
Exercício
Exercícios
Circunferência
Circulo
Elementos de um Circulo
Posições relativas de retas e circunferência
Posições relativas de retas e circunferência
Posições relativas de retas e circunferência
Ângulo central
Medida do ângulo central e do arco correspondente
Medida do ângulo central e do arco correspondente
Medida do ângulo central e do arco correspondente
Ângulo inscrito
Ângulo inscrito
Prova:
Três casos a considerar
Ângulo inscrito