COMANDO DA AERONÁUTICA DEPARTAMENTO DE ENSINO DA

COMANDO DA AERONÁUTICA
DEPARTAMENTO DE ENSINO DA AERONÁUTICA
ESCOLA PREPARATÓRIA DE CADETES DO AR
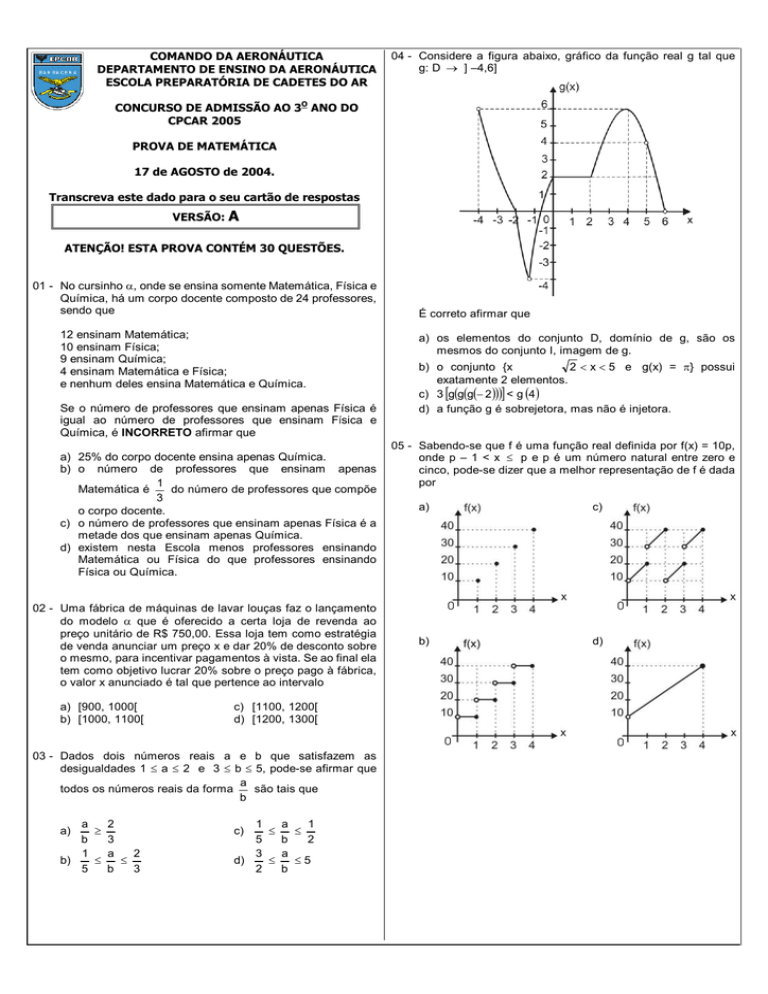
04 - Considere a figura abaixo, gráfico da função real g tal que
g: D → ] –4,6]
CONCURSO DE ADMISSÃO AO 3O ANO DO
CPCAR 2005
PROVA DE MATEMÁTICA
17 de AGOSTO de 2004.
Transcreva este dado para o seu cartão de respostas
VERSÃO: A
ATENÇÃO! ESTA PROVA CONTÉM 30 QUESTÕES.
01 - No cursinho α, onde se ensina somente Matemática, Física e
Química, há um corpo docente composto de 24 professores,
sendo que
12 ensinam Matemática;
10 ensinam Física;
9 ensinam Química;
4 ensinam Matemática e Física;
e nenhum deles ensina Matemática e Química.
Se o número de professores que ensinam apenas Física é
igual ao número de professores que ensinam Física e
Química, é INCORRETO afirmar que
a) 25% do corpo docente ensina apenas Química.
b) o número de professores que ensinam apenas
1
Matemática é
do número de professores que compõe
3
o corpo docente.
c) o número de professores que ensinam apenas Física é a
metade dos que ensinam apenas Química.
d) existem nesta Escola menos professores ensinando
Matemática ou Física do que professores ensinando
Física ou Química.
02 - Uma fábrica de máquinas de lavar louças faz o lançamento
do modelo α que é oferecido a certa loja de revenda ao
preço unitário de R$ 750,00. Essa loja tem como estratégia
de venda anunciar um preço x e dar 20% de desconto sobre
o mesmo, para incentivar pagamentos à vista. Se ao final ela
tem como objetivo lucrar 20% sobre o preço pago à fábrica,
o valor x anunciado é tal que pertence ao intervalo
a) [900, 1000[
b) [1000, 1100[
É correto afirmar que
a) os elementos do conjunto D, domínio de g, são os
mesmos do conjunto I, imagem de g.
b) o conjunto {x i þ s 2 < x < 5 e g(x) = π} possui
exatamente 2 elementos.
c) 3 [g(g(g(− 2 )))] < g (4 )
d) a função g é sobrejetora, mas não é injetora.
05 - Sabendo-se que f é uma função real definida por f(x) = 10p,
onde p – 1 < x ≤ p e p é um número natural entre zero e
cinco, pode-se dizer que a melhor representação de f é dada
por
a)
c)
0
b)
d)
c) [1100, 1200[
d) [1200, 1300[
0
03 - Dados dois números reais a e b que satisfazem as
desigualdades 1 ≤ a ≤ 2 e 3 ≤ b ≤ 5, pode-se afirmar que
a
todos os números reais da forma
são tais que
b
a
2
≥
b
3
1
a
2
b)
≤
≤
5
b
3
a)
0
1
a
1
≤
≤
5
b
2
3
a
d)
≤
≤5
2
b
c)
0
CPCAR 2005
MATEMÁTICA - 3º ANO - VERSÃO A
06 - Analise os itens abaixo, referentes a funções reais.
(01)
A função f definida por f(x) = 3x 2 + 4x é par
(02)
Se g é definida por g(x) = 2x + 8, então g(x) > 0,
∀x> – 4
(04)
O conjunto-imagem da função h, definida por
x
h(x) =
é Im = {y g þ s y ≠ 1}
x −1
x −1
Se f é dada por f(x)=
, para todo x diferente de
2−x
2x + 1
2, então f −1 (x)=
, para todo x diferente de –1
x +1
(08)
2
10 - Em þ, o conjunto solução da inequação sx + 1s – sxs ≤ x +
2é
c) [–3, +∞[
d) [–3, 0] N {x g þ s x S 1}
a) [–3, 0]
b) {x g þ s x R 0} N [3, 5]
11 - Uma população de bactérias cresce conforme a função
αt
definida por N(t) = N0 . e , onde t é o tempo (dado em
horas), N0 é o número inicial de bactérias e α é uma
constante positiva. Sabendo-se que o número de bactérias
triplica ao final das três primeiras horas, pode-se dizer que α
pertence ao intervalo
Dados: adote e = 2,7 (e é a base do sistema de logaritmos
neperianos)
A soma dos itens verdadeiros é
a) 15
b) 14
log 3 = 0,48
c) 13
d) 8
a)
b)
[0,3; 0,4]
] 0,4; 0,5]
c)
d)
] 0,5; 0,6]
] 0,6; 0,7]
o
07 - Alguns alunos do 3 ano da EPCAR desejam fazer uma
viagem durante um recesso e para isso precisam fretar um
ônibus.
Duas empresas, α e β , candidatam-se para fazer a viagem.
Sabendo-se que as duas empresas possuem ônibus de 50
lugares e que: se for contratada a empresa α, o custo da
viagem terá uma parte fixa de R$ 300,00, mais um custo por
passageiro de R$ 15,00; se for contratada a empresa β , o
custo terá um valor fixo de R$ 250,00, mais um custo(C),
por passageiro, dado por C(n) = 35 – 0,5n, onde n é o
número de passageiros que fará a viagem.
12 - Assinale a alternativa correta.
a) Se x > 0 e a > 1, os gráficos das funções reais f e g,
x
 1
dadas por f(x) = loga x e g(x) =   , se interceptam em
a
um ponto cuja abscissa é maior que zero e menor
que um.
b) Para qualquer que seja x real, o intervalo ]–4, +∞[ é o
conjunto-imagem da função real h, definida por
x +1
Com base nisso, é correto afirmar que
a) se todos os lugares forem ocupados, será menos
vantajoso contratar a empresa β .
b) existe um determinado número n de passageiros para o
qual o custo na empresa α é o mesmo da empresa β .
c) o custo máximo da viagem na empresa β é de R$ 862,50
d) para um custo de R$ 750,00, a empresa β levará um
número de passageiros 50% maior que a empresa α.
 1
h( x ) =  
−4
2
c) Se log9(log3 (logx 3)) = 0, então x é um número racional.
–x
d) Se f é uma função real definida por f(x) = 3 + 2 , então
1
f(log4 9) é igual a
3
13 - O
08 - A
soma
dos
quadrados das raízes da equação
104
5x – 2px – p = 0 é
. Vale então dizer que o valor
25
positivo de p é um número
2
a) par
b) primo maior que 10
c) divisor de 15
d) menor que 1
domínio
da
função
real
definida
por
f ( x ) = log 1 loga (loga x ) é
a
a)
b)
c)
d)
a
a < x R a se 0 < a < 1
a
0 < x < 1 e x S a se a > 1
a
a < x R a se a > 1
a
x S a se 0 < a < 1
09 - C o n s i d e r a n d o a f u n ç ã o r e a l f , d e f i n i d a p o r
f(x) = sx –2s + s2x + 1s – x – 6, é I N C O R R E T O
afirmar que
a) seu conjunto-imagem é [–3, +∞[
b) f é bijetora ⇔ x ≥ 2
5
c) se f(x) = 5 , então x = –
ou x = 6
2
d) o intervalo em que f decresce é ] − ∞, −
1
]
2
14 - Em um casarão abandonado, um portão medindo 3 m de
CPCAR 2005
MATEMÁTICA - 3º ANO - VERSÃO A
altura por 2 m de largura se abre bruscamente girando 30°,
conforme figura abaixo.
3
assinale a alternativa correta.
(I)
(II)
(III)
f(x) = senx + ssenxs; 0 ≤ x ≤ 2 π
g(x) = 2scosxs; 0 ≤ x ≤ 2 π
h(x) = 2ssen2xs; 0 ≤ x ≤ 2π
Esse fato faz com que uma aranha, seguindo sua teia, se
desloque da posição A para a posição B’, sendo A’ e B’,
respectivamente, as extremidades superior e inferior do
portão após o processo.
É correto afirmar que a distância que separa A e B’, em
metros, é igual a
a) I(m), II(p), III(q)
b) I(m), II(n), III(p)
a)
17 − 4 3
c)
11+ 3
b)
11− 3
d)
17 + 4 3
c) I(n), II(m), III(p)
d) I(q), II(m), III(n)
17 - A figura abaixo representa o ciclo trigonométrico com os
eixos da tangente e cotangente destacados.
15 - Analise as afirmativas seguintes classificando-as em (V)
verdadeiras ou (F) falsas.
Se tg x = –2, então sec x + sen x vale 2
1
II - A equação sen x . cos x =
no intervalo [0, 2π] possui
4
4 raízes.
0
0
1
2
π
III - Se x + y =
, então cos x sen x 0 é igual a
3
2
sen y cos y 0
I-
É correto afirmar que apenas
a) I é verdadeira.
b) I e II são verdadeiras.
c) II e III são verdadeiras.
d) II é verdadeira.
16 - Associando a função com sua representação gráfica,
Depois de encontrar o valor de a, o conjunto solução da
inequação scos xs < – a é
a) − {kπ, k ∈ }
c) þ
b) ∅
d) { x ∈ x ≠
π
+ kπ, k ∈ }
2
18 - Analise as proposições abaixo, classificando-as em (C)
CPCAR 2005
MATEMÁTICA - 3º ANO - VERSÃO A
certas ou (E) erradas.
13π
resulta em valor
9
( ) A expressão cos 5485° + cossec
negativo.
1
1

sen  2 x +  é o
2
2

período
da
função
( ) O período da função f(x) = 2 +
quádruplo
do
1 
1
tg  4 x + 
4 
4
( ) Se sec x = a, então sec(–x) = – a
4
x + 4 y = a2 − 4a

22 - Seja o sistema de variáveis x, y e z: 2 y + az = 0

x + a2 z = 0
Para que ele seja homogêneo e admita somente a terna
(0, 0, 0) como solução, o valor de a deve ser igual a
a) 0
b) 2
c) 3
d) 4
g( x ) = 4 +
π

( ) O domínio da função f(x) = tg  2 x −  é igual ao
3


π
domínio da função g(x) = 2 –
cotg x.
3
A seqüência correta é
a) C, C, E, E
b) E, E, E, C
c) C, C, C, E
d) E, C, C, E
19 - Em uma seqüência de 10 números, a1, a2, ..., a9, a10, os sete
primeiros termos estão em progressão aritmética de primeiro
termo 1, os três últimos termos estão em progressão
geométrica, cujo primeiro termo é 7.
Sabendo-se que a7 = a8 e a6 = a9, a soma dos termos dessa
seqüência é um número entre
a) 45 e 46
b) 46 e 47
c) 47 e 48
d) 48 e 49
20 - O valor da expressão
r 2 + r 4 + r 6 + ... + r 2n
, para n i û*, é
1
1 1
1
+
+
+
...
+
r2 r 4 r6
r 2n
2n+1
a) r
2n
b) r
c) r
2+2n
d) r
23 - Foram vendidos 240 ingressos para uma seção de circo. A
arrecadação foi de R$1840,00 e todos os espectadores
pagaram ingresso. O preço para homem adulto é R$10,00,
para mulher adulta, R$8,00, e para criança, R$4,00. Se a
soma entre o número de mulheres adultas e crianças
equivale ao dobro do número de homens adultos, é correto
afirmar que
a) havia mais crianças do que mulheres adultas no circo.
b) a seqüência (número de crianças, número de homens
adultos, número de mulheres adultas) é, nesta ordem,
uma progressão aritmética de razão 20.
c) havia 100 homens adultos no circo.
d) havia 40 crianças, 80 homens adultos e 120 mulheres
adultas no circo.
24 - Uma prova consta de 10 proposições. Cada uma delas deve
ser classificada como verdadeira (V) ou falsa (F). O número
de maneiras de se classificar as 10 questões dessa prova, a
fim de se obter pelo menos 70% de acertos é
a) 120
b) 175
25 - Um grupo de 6 amigos (A, B, C, D, E, F) compra 3 entradas
para um show. Para serem escolhidos os 3 amigos que irão
ficar com essas entradas, foi feito um sorteio.
A probabilidade de A ser sorteado e B não, é igual a
7
10
1
b)
20
a)
21 - Sejam A, B, C matrizes reais não-nulas de ordem 2,
satisfazendo às seguintes relações:
–1
–1
1ª) AB = C , em que C
1
A
2ª) B =
2
b)
1
2
2
2
1
2
3
d)
10
c)
é a inversa de C
26 - Analise as afirmativas abaixo
verdadeiras (V) ou falsas (F).
Se o determinante de C é 16, então o valor do módulo do
determinante de A é igual a
a)
c) 176
d) 186
c)
d)
1
8
2
4
e
classifique-as
em
Um salão de festas tem 6 portas. O número de modos
de ele estar aberto (o que acontece se, pelo menos
uma porta estiver aberta) é 64.
II - Com os algarismos do sistema decimal, pode-se formar
16 números de 2 algarismos, sendo que o algarismo
das dezenas corresponde a um múltiplo de 2 (diferente
de zero) e que o algarismo das unidades corresponde a
um múltiplo de 3.
III - Duas pessoas entram em um ônibus onde há 5 lugares
vagos. Elas podem ocupar estes lugares de 10
maneiras distintas.
I-
Tem-se que
a) apenas I é verdadeira.
b) apenas II é verdadeira.
c) apenas III é verdadeira.
d) todas são falsas.
CPCAR 2005
MATEMÁTICA - 3º ANO - VERSÃO A
27 - Se n é o número de termos do desenvolvimento de
(
5
x + 10 y
a) 4
b) 5
)
55
que não contém radical, então n vale
c) 6
d) 7
28 - Em um tubo cilíndrico de altura h = 20 cm e raio interno da
base r = 2 cm, colocam-se esferas tangentes ao mesmo e
tangentes entre si, de tal forma que a altura do cilindro seja
igual a soma dos diâmetros das esferas nele contidas. O
3
volume interior ao cilindro e exterior às esferas vale, em cm ,
102π
3
80π
b)
3
a)
c) 40 π
d)
160π
3
29 - Sobre o estudo da Geometria Espacial, é INCORRETO
afirmar que
a) dados três pontos não-colineares do espaço, existe um, e
somente um, plano que os contém.
b) por um ponto passa uma única reta perpendicular a um
plano dado.
c) se dois planos são perpendiculares, toda reta de um
deles que for perpendicular à interseção dos dois planos
será perpendicular ao outro.
d) se dois planos distintos são paralelos, qualquer reta de
um deles é paralela a qualquer reta do outro.
30 - Em uma pirâmide P quadrangular regular, cujo volume é
3
igual a 360 dm , numa seção paralela à base inscreve-se um
45π
2
círculo cuja área é
dm . Se tal seção foi feita a 3 dm do
4
vértice, é correto afirmar que a altura da pirâmide P, em
decímetros, é um número do intervalo
a) [4, 5[
b) [5, 6[
c) [6, 7[
d) [7, 8]
5