Simulado

08 de Novembro de 2013
Simulado
1
Simulado
1. De acordo com seus conhecimentos matemáticos assinale a
soma das afirmações verdadeiras :
01. Dadas as funções reais de variável real f(x) = mx + 1 e g(x) = x + m, onde m é uma constante real com 0 < m < 1, temos
que (f % g) (x) = (g % f) (x), para algum x real.
02. Seja a equação: 3(log x) + 1 -- 3(log x) -- 1 + 3(log x) -- 3 -- 3(log x) -- 4 = loge e . Sabe-se que loge x é igual à maior raiz da equação r² – 4r – 5 = 0. O
e
e
e
e
sen a
-- 657
valor de a para que a equação seja verificada é arc sen 13 .
e
04.Para que a equação 10x² + bx + 2 = 0 não admita raízes reais, b deve satisfazer a condição – 8 5 < b < 8 5 .
08.O menor valor inteiro de x que satisfaz a inequação x 2 -- x > 1 – x
é um número primo.
2
Simulado
2. Sobre matrizes, determinantes e sistemas lineares, assinale a
soma das afirmações verdadeiras :
01. Sabendo que para que o sistema dado seja indeterminado, teremos m = a/b e p = c, teremos a + b + c = 21.
)
2x + 3 + y = my -- 1
4x -- 2y + p = 2 + 5y
02. Sendo o sistema abaixo impossível, teremos que os valores
absolutos de a, b e c serão números consecutivos, onde p = a e
m ≠ b/c.
)
3x + 2y = 4m + 4
6x -- (p + 2) y = 1
R V
04.Seja a matriz A = SSa b WW onde a = 2(1 + log 5) ; b = 2log 8 ; c = log 3 81 e
Tc d X
d = log 3 27 . Uma matriz real quadrada
R B, de Vordem 2, tal que AB
S-- 3 2 W
é a
matriz identidade de ordem 2 é: S 2 5 W.
W
SS 2
2W
T
X
R 2
V R
V
cos x sen x W Ssen x 0 W
08.Se SS
=
, então para todo x ! r + kr , k
4
2
a sen x a W S -- 1 2 cos x W
T
X T
X
inteiro, o valor de a é tg 2x
2
08 de Nov de 2013
2
3
3. Um sargento quer colocar os seus soldados em filas formando
um quadrado. Tendo colocado um certo número de soldados
em cada fila, sobraram 39 soldados; colocando mais um soldado em cada fila ficaram, então,faltando 50 soldados para completar o quadrado. A soma dos algarismos do número que representa a quantidade de soldados do batalhão é:
4
Simulado
4. No dia a dia a matemática se faz presente das maneiras mais
inusitadas, analise os casos abaixo e assinale a soma das afirmações verdadeiras:
01. Com vinhos de R$ 9,00 e R$ 12,00 o litro, queremos fazer uma mistura de 120 litros ao preço médio de R$ 11,00 o litro. A quantidade
de litros de um dos tipos de vinho será o dobro da quantidade
do outro.
02. Uma torneira enche um tanque em 12 minutos, enquanto uma
segunda torneira gasta 18 minutos para encher o mesmo tanque. Com o tanque inicialmente vazio, abre–se a primeira torneira durante x minutos; ao fim desse tempo, fecha–se essa
torneira e abre-se a segunda, a qual termina de encher o tanque em x + 3 minutos. O tempo gasto para encher o tanque todo será um número múltiplo de 6.
04.Entre todos os números de 4 algarismos distintos, sendo que
“x” deles possuem um algarismo ímpar na ordem das centenas
e um algarismo ímpar na ordem das dezenas. O valor de “x” é
um número cuja soma dos seus algarismos será par.
08.Um professor dispunha de 144 doces para dividir igualmente
entre os alunos de sua classe. Como no dia da distribuição faltaram 12 alunos, ele dividiu os 144 doces igualmente entre os
presentes, cabendo a cada aluno 1 doce a mais. A quantidade
de alunos presentes no dia da distribuição é um número que
é um quadrado perfeito.
08 de Nov de 2013
5
5. Em certas ocasiões a matemática parece agir de maneira completamente abstrata e distante da realidade, mas na verdade
isto nunca ocorre, basta conhecimento para associa-la. Assinale a soma das afirmações verdadeiras:
01. Sabendo que z ≠ 0, 3x – 4y + 6z = 0 e 2x + 5y – 19z = 0, o valor numérico da expressão:
2x 2 -- 5xy
será uma fração irredutível cuja soz 2 -- y 2
ma do numerador com o denominador será um número primo
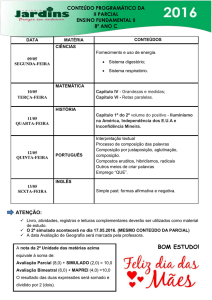
02. o triângulo retângulo ABC da figura, b = 1 e c = 2. Então, x é um
número irracional.
04.Consideremos a equação ^ tg ahcos
2
x -- (cos x)Lb + 8(lb) 2
= ^cotg ah-- 2(Lb) onde
2
r < a < r , a fixado, b > 0. A equação acima tem solução em x
4
2
se − 1/6< Lb < 1/6.
08.Se log 2 = 0,3010 e 2 x -- 2 = 16 , então o número de algarismos de 2x
é um número primo.
6
Simulado
08 de Nov de 2013
7
nome
semi
extensivo
grupo
top100
intensivo
1
2
3
4
5