Lista de Exercícios de Aula

Lista de Exercícios de Aula
Número da aula: .................................................................................9
Módulo: ........................................................................ SL – Simulado
Atividade:................................................................... 2 – Simulado 2
TEMPORADA 2017
estudematematica.com.br
01. O produto de dois números positivos consecutivos é
240. O dobro do máximo divisor comum desses
números é igual a
(A)
(B)
(C)
(D)
(E)
1
2
30
240
480
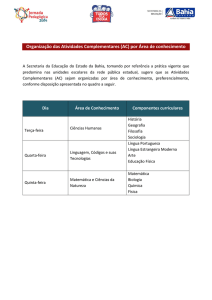
02. Uma empresa de entrega de mercadorias possui
várias filiais em uma cidade. A fim de maximizar a
distribuição, a empresa dividiu a cidade em 305
setores, designando um número natural a cada setor.
A tabela abaixo mostra parte do quadro de
distribuição de uma das filiais desta empresa, sendo
que os demais setores seguem a forma de
distribuição apresentada.
Dias da Semana
Segunda-feira
Terça-feira
Quarta-feira
Quinta-feira
Sexta-feira
Sábado
Setor
7
1
6
2
13
12
8
5
3
14
11
9
4
15
10
Essa filial atenderá o setor 275 em uma
(A)
(B)
(C)
(D)
(E)
quinta-feira
terça-feira
segunda-feira
sexta-feira
quarta-feira
LEA-2017-09-SL2
Estu dar M atemátic a pode se r l eg al!
www.estudematematica.com.br
1/4
03. Sendo a e b dois números reais, com a ≠ ±b ≠ 0 , a
expressão
a + b a 2b − ab 2
é equivalente a
⋅
a 2 − ab a 2b − b3
(A) 1
1
a−b
1
(C)
a+b
(D) a − b
(E) a + b
(B)
04. O número que deve ser somado ao numerador e ao
2
denominador da fração
para que ela tenha um
3
aumento de 20% é
(A)
(B)
(C)
(D)
(E)
1
2
3
4
5
05. Seja S = {S1 ,S2 ,S3 } o conjunto de sintomas de uma
determinada doença. Em geral, um portador dessa
doença apresenta apenas um subconjunto não vazio
de S. A alternativa que corresponde ao número de
subconjuntos de S que poderão apresentar os
pacientes portadores dessa doença é
(A)
(B)
(C)
(D)
(E)
7
8
16
15
2
LEA-2017-09-SL2
Estu dar M atemátic a pode se r l eg al!
www.estudematematica.com.br
2/4
06. Uma função real f do primeiro grau é tal que
f ( 0 ) = 1+ f (1) e f ( −1) = 2 − f ( 0 ) . Então f ( 3) é
igual a
(A) −3
7
(B)
2
(C) −1
(D) 0
5
(E) −
2
07. Uma função quadrática tem o eixo dos y como eixo
de simetria. A distância entre os zeros da função é de
4 unidades, e a função tem −5 como valor mínimo.
Esta função quadrática é
(A)
(B)
(C)
y = 5x 2 − 4x − 5
5
y = x 2 − 5x
4
5 2
y = x − 20
4
(D) y = 5x 2 − 20
(E)
5
y = x2 −5
4
08. Dada a função
f
( 2)
= f!f ,
f
( 3)
f ( x ) = x + 2 , com
= f!f!f ,
f
(4)
assim por diante, então o valor de f
(A)
(B)
(C)
(D)
(E)
x ∈! . Se
= f!f!f!f
(102)
e
(1) é
103
249
307
199
205
LEA-2017-09-SL2
Estu dar M atemátic a pode se r l eg al!
www.estudematematica.com.br
3/4
09. Considerando que 101,079 = 12 , o valor de x que
satisfaz a equação 12 x = 100 é
(A) 2
(B) 1,079
2
(C)
1,079
(D) 0,79
(E) 0,12
10. A raiz real da equação log 3 ( 9 x − 2 ) = x é
(A) log 3 2
(B)
2log 3 2
⎛ 2⎞
(C) log 3 ⎜ ⎟
⎝ 3⎠
(D) log 3 2
(E)
log 3 3
LEA-2017-09-SL2
Estu dar M atemátic a pode se r l eg al!
www.estudematematica.com.br
4/4