Ângulos no plano

Curso de linguagem matemática – Professor Renato Tião
Exercícios de treinamento
6. Sabendo que ângulos geométricos têm medidas
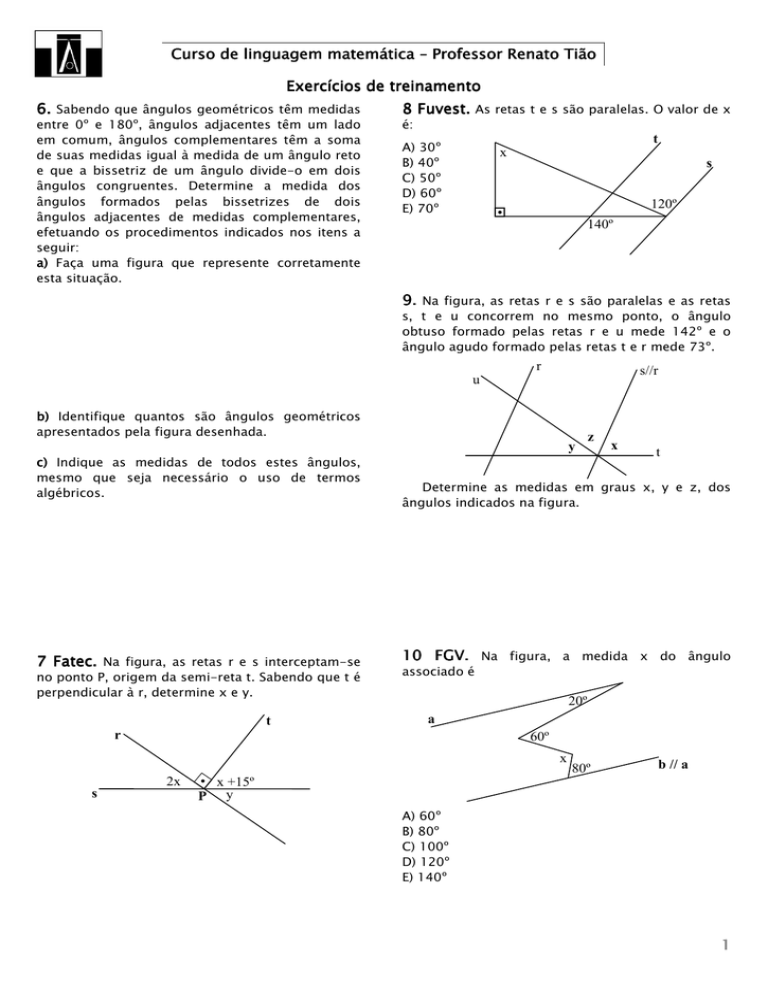
8 Fuvest. As retas t e s são paralelas. O valor de x
entre 0º e 180º, ângulos adjacentes têm um lado
em comum, ângulos complementares têm a soma
de suas medidas igual à medida de um ângulo reto
e que a bissetriz de um ângulo divide-o em dois
ângulos congruentes. Determine a medida dos
ângulos formados pelas bissetrizes de dois
ângulos adjacentes de medidas complementares,
efetuando os procedimentos indicados nos itens a
seguir:
a) Faça uma figura que represente corretamente
esta situação.
é:
t
A) 30º
B) 40º
C) 50º
D) 60º
E) 70º
x
s
120º
140º
9. Na figura, as retas r e s são paralelas e as retas
s, t e u concorrem no mesmo ponto, o ângulo
obtuso formado pelas retas r e u mede 142º e o
ângulo agudo formado pelas retas t e r mede 73º.
r
s//r
u
b) Identifique quantos são ângulos geométricos
apresentados pela figura desenhada.
y
c) Indique as medidas de todos estes ângulos,
mesmo que seja necessário o uso de termos
algébricos.
7 Fatec. Na figura, as retas r e s interceptam-se
no ponto P, origem da semi-reta t. Sabendo que t é
perpendicular à r, determine x e y.
t
x
t
Determine as medidas em graus x, y e z, dos
ângulos indicados na figura.
10 FGV. Na figura, a medida x do ângulo
associado é
20º
a
r
60º
x
2x
s
z
P
80º
b // a
x +15º
y
A) 60º
B) 80º
C) 100º
D) 120º
E) 140º
1
Curso de linguagem matemática – Professor Renato Tião
11 Fuvest. No retângulo a seguir, o valor, em
12 Fuvest. No triângulo ACD da figura, B é um
graus, de α+β é:
ponto do lado AD tal que AB=BC=CD. Sendo x a
medida do ângulo interno de vértice A e y a medida
do ângulo externo de vértice C, podemos afirmar
que:
40º
C
β
y
α
A) 50
B) 90
C) 120
D) 130
E) 220
Solução 1:
A
x
D
B
A) x = y
B) x = 2y
C) x = 3y
D) y = 2x
E) y = 3x
13 Fuvest. Na figura a seguir Â=36º, AB=AC e
CB=CD.
C
A
Solução 2:
D
B
a) Calcule as medidas dos ângulos DCB e ADC.
b) Prove que AD=BC.
Solução 3:
2
Curso de linguagem matemática – Professor Renato Tião
14. Na figura a seguir os segmentos AC e BD
interceptam-se no ponto E. Além disso, temos que
AB=AC=AD, BÂC=20º e CÂD=50º.
A
17. Na figura a seguir, ABCD é um paralelogramo
de ângulo agudo Â=20º em que M é o ponto médio
do lado BC, P é um ponto do lado CD tal que
CP=CM.
P
D
20º 50º
B
C
M
α
E
C
x
20º
A
β
D
a) Quantos são os triângulos apresentados por esta
figura?
b) Quais destes triângulos são isósceles, e quais
são suas bases?
c) Calcule as medidas α e β.
Q
B
Sendo BQ perpendicular à reta PM podemos
afirmar que a medida x do ângulo MBQ vale:
A) 10º
B) 12º
C) 15º
D) 18º
E) 20º
18. Seja x a medida, em graus, do ângulo formado
pelas semi-retas r e s de origem no vértice A do
triângulo retângulo ABC como mostra a figura.
A
x
r
s
B
C
Sendo R e S os pontos em que as semi-retas r e
s interceptam a hipotenusa BC, e sabendo que o
menor ângulo agudo do triângulo mede 20º calcule
o valor de x nos seguintes casos:
15. Num trapézio isósceles ABCD, a base menor
BC tem a mesma medida que os lados não
paralelos AB e CD; e a base maior AD tem a mesma
medida que as diagonais AC e BD. A medida do
maior ângulo interno deste trapézio é:
A) 108°
B) 120°
C) 130°
D) 135°
E) 144°
a) AR é altura e AS é bissetriz interna do ∆ ABC.
b) AR é altura e AS é mediana do ∆ABC.
16. Num trapézio isósceles, as bases medem 12 m
e 8 m e as diagonais são bissetrizes dos ângulos
da base maior. Então, o perímetro desse trapézio é
de:
c) AR é mediana e AS é bissetriz interna do ∆ABC.
A) 16 m
B) 26 m
C) 36 m
D) 46 m
E) 56 m
3
Curso de linguagem matemática – Professor Renato Tião
19. O ângulo oposto à base BC do triângulo
isósceles ABC mede 80º. Determine as medidas
dos ângulos formados nas intersecções da altura
AH deste triângulo com:
21. Sendo P um ponto do interior do triângulo ABC
tal que os ângulos PBA e PCA medem 30º e 50º
respectivamente, determine a diferênça entre as
medidas dos ângulos BPC e BAC.
a) a bissetriz interna do ângulo B.
22. O ponto médio M da base BC do triângulo ABC
é vértice do quadrado MNPQ cujo perímetro é igual
ao dobro da medida BC. Os vértices N e Q deste
quadrado pertencem aos lados AB e AC do triângulo
ABC como mostra a figura.
A
b) a mediatriz do lado AB.
P
N
Q
B
M
C
A medida em graus do ângulo interno de vértice
A do triângulo ABC é
c) o segmento BD, sendo D um ponto do lado AC
tal que BD = AC.
A) 15º
B) 20º
C) 30º
D) 45º
E) 60º
23. Considere um quadrado ABCD e dois triângulos
equiláteros: ABP no interior do quadrado e BCQ
exterior ao quadrado. Prove que o ponto P pertence
ao segmento QD.
20 Unesp. Considere o triângulo ABC da figura:
A
50º
B
C
Se a bissetriz interna do ângulo B forma com a
bissetriz externa do ângulo C um ângulo de 50º,
determine a medida do ângulo interno A.
4
Curso de linguagem matemática – Professor Renato Tião
24. Uma folha de um caderno retangular foi
27. Na figura a seguir, os arcos QMP e MTQ
dobrada formando, em sua base, um ângulo de 30º
conforme a figura. Calcule as medidas dos ângulos
internos do triângulo determinado pela dobra.
medem, respectivamente, 170° e 130°. Então, o arco
MSN mede:
30º
25. Um pedaço de cartolina, branco de um lado e
cinza do outro, tem a forma de triângulo equilátero
que foi dobrado de modo que um de seus vértices
encontre o lado oposto como mostra a figura:
A) 60°
B) 70°
C) 80°
D) 100°
E) 110°
28. Sendo P o centro da circunferência que
circunscreve
o
hexágono
regular
ABCDEF,
determine as medidas dos ângulos formados nos
cruzamentos das seguintes retas:
a) AC e BF.
α
b) AC e BP.
c) BD e EF.
β
Sendo α e β as medidas em radianos dos
ângulos indicados na figura, pode-se afirmar que:
A) 3α + 3β = π
B) 6α + 3β = π
C) –3α + 6β = π
D) 3α + 6β = π
E) 6α – 3β = π
26 Fuvest. Os pontos B, P e C pertencem À
circunferência γ e BC é lado de um polígono regular
inscrito em γ.
29.
Dados
n
pontos
que
dividem
uma
circunferência em partes iguais, podemos obter
formas geométricas poligonais e regulares ligando
estes pontos por meio de segmentos de diversas
maneiras.
Cada uma dessas maneiras é designada por um
número p que é chamado de passo de ligação. As
figuras a seguir apresentam circunferências
divididas em partes iguais por 9 pontos ligados com
passos 1, 2, 3 e 4.
Sabendo-se que o ângulo BPC mede 18º,
podemos concluir que o número de lados do
polígono é igual a
A soma das medidas, em radianos, dos nove
ângulos geométricos com vértices sobre a
circunferência, em cada figura, pode obtida pela
expressão:
A) 6
B) 7
C) 10
D) 12
E) 14
A) (8 − p) ⋅ π
B) (6 + p) ⋅ π
C) (9 − 2p) ⋅ π
D) (4 + 3p) ⋅ π
E) (10 − 3p) ⋅ π
5
Curso de linguagem matemática – Professor Renato Tião
30. Um pedaço de papel na forma de um
32. Considere um eneágono regular ABCDEFGHI
paralelogramo é tal que pode ser dobrado
formando um pentágono regular. Para isto, basta
fazer coincidir as extremidades da sua diagonal
maior como mostram as figuras a seguir.
inscrito numa circunferência de
responda às seguintes perguntas:
Vinco da
dobradura
centro
O
e
V
Figura 1
Figura 2
Sabendo que cada ângulo interno de um
pentágono regular mede 108º e que o vinco da
dobradura é perpendicular ao vetor V que, na
figura 1, representa a maior diagonal do
paralelogramo, pode-se concluir que a inclinação,
em graus, deste vetor em relação ao lado menor do
paralelogramo é igual a:
A) 72
B) 63
C) 54
D) 45
E) 36
b) Quanto vale a soma de seus ângulos externos?
c) Quanto mede cada um de seus ângulos externos?
d) Quanto mede cada um de seus ângulos internos?
e) Quanto mede o ângulo AÔD?
f) Quanto mede o ângulo BÂC?
g) Qual é a medida do ângulo interno do vértice do
polígono estrelado que se obtém prolongando-se
os seus lados?
31. Chamamos de formas modulares às figuras
geométricas planas ou espaciais capazes de
preencher completamente o plano ou o espaço,
quando uma infinidade delas é colocada lado a
lado. Assim, o decágono irregular, composto por
um octógono regular e um quadrado de mesmo
lado como mostra a figura, é uma forma modular:
Há apenas onze maneiras de se preencher o
plano usando apenas de polígonos regulares, e
apenas três delas o fazem com um único tipo de
polígono:
a) Justifique matematicamente o fato de
triângulos equiláteros, os quadrados e
hexágonos regulares serem formas modulares.
a) Quanto vale a soma de seus ângulos internos?
Desafio
33. A figura apresenta um octógono regular e um
pentágono regular com um lado em comum.
Determine as medidas dos ângulos x, y, z e w
indicados na figura.
y
w
z
x
os
os
b) Explique por qual motivo o pentágono regular
não é forma modular.
c) Apresente uma forma modular composta por
dois tipos de polígono regular que não seja a
sugerida pelo enunciado.
6