números complexos em eletrônica

NÚMEROS COMPLEXOS EM ELETRÔNICA
Formulário para circuitos AC
É uma forma na qual se inclui ângulo de fase e magnitude de uma ou mais grandezas.
Uma expressão complexa compreende uma parte real e uma parte imaginária, conforme
mostra a figura abaixo.
j é um operador que varia de 0º a 360º, em ângulos de 90º.
O ângulo de 90º é de grande importância na análise de circuitos AC.
1) + 4 indica 4 unidades a 0º
2) - 4 indica 4 unidades a 180º
3) j4 indica 4 unidades a 90º
Como j é um operador a 90º, isto significa que em 180º ele é repetido 2 vezes, em 270º é
repetido 3 vezes e assim por diante.
RESUMINDO
0º = 1
90º = + j
180º = j2 = - 1
270º = j3 = j2. j = - 1. j = - j
360º = 0º = 1
Números Complexos em Eletrônica – Prof. Edgar Zuim
Página 1
A expressão complexa deve ser escrita da seguinte forma: parte real ± parte complexa onde j
é sempre escrito antes do número.
Exemplo:
4 ± j2
RELAÇÃO DO FASOR COM A FORMA RETANGULAR
3 representa um número real ( neste caso uma resistência de valor igual a 3Ω);
o ângulo de 90º ou +j é usado para representar XL (4Ω);
portanto: Z = 3 + j4
como no caso anterior, 3 representa uma resistência no valor de 3Ω;
o ângulo de - 90º ou - j é usado para representar XC (4Ω);
portanto: Z = 3 - j4
Podemos então representar circuitos na forma complexa retangular conforme exemplos
abaixo:
Z2 = R2 + XL2
Z = 8 + j5
Números Complexos em Eletrônica – Prof. Edgar Zuim
Z2 = R2 + XC2
Z = 10 - j6
Página 2
IT2 = IR2 + IC2
IT = 1 + j3
IT2 = IR2 + IL2
IT = 1 - j3
O operador j indica uma relação de fase diferente de zero entre a parte real e a parte
imaginária.
Tomemos como exemplo impedâncias:
Se R = 0 e XC = 10Ω  Z = 0 - j10
Se R = 10Ω e XC = 0  Z = 10 - j0
Se R = 0 e XL = 10Ω  Z = 0 + j10
Se R = 10Ω e XL = 0  Z = 10 + j0
Vejamos alguns exemplos abaixo de circuitos mais complexos:
ZT = (9 + j6) + (3 - j2)
ZT = 12 + j4
1 1 1
1
= +
+
ZT 4 j8 - j 5
Números Complexos em Eletrônica – Prof. Edgar Zuim
Página 3
ZT =
(9 + j 5) . (3 - j 2)
(9 + j 5) + (3 - j 2)
OPERAÇÕES COM NÚMEROS COMPLEXOS
I - ADIÇÃO OU SUBTRAÇÃO:
Soma-se ou subtrai-se a parte real e a parte imaginária ( j ) separadamente:
a) (9 + j5) + (3 + j2)  (9 + 3) + (j5 + j2) = 12 + j7
b) (9 + j5) + (3 - j2)  (9 + 3) + (j5 - j2) = 12 + j3
c) (9 + j5) + (3 - j8)  (9 + 3) + (j5 - j8) = 12 - j3
II - MULTIPLICAÇÃO OU DIVISÃO DE UM NÚMERO IMAGINÁRIO
( termo j ) POR UM NÚMERO REAL
Basta multiplicar ou dividir, conforme exemplos abaixo:
a) 4 . j3 = j12
b) j5 . 6 = j30
c) j5 . -6 = -j30
d) j12 ÷ 3 = j4
e) -j30 ÷-6 = j5
f) j30 ÷ -6 = -j5
g) j3 ÷ 4 = j0,75
h) 1,5 . j2 = j3
i) 4 . j0,75 = j3
III - DIVISÃO DE UM NÚMERO IMAGINÁRIO POR UM NÚMERO
IMAGINÁRIO ( divisão de um termo j por um termo j )
A divisão produzirá um número real ( as partes imaginárias ou os termos j se cancelarão),
conforme exemplos abaixo:
a) j12 ÷ j3 = 4
b) j30 ÷ j5 = 6
c) - j12 ÷ j3 = - 4
d) j30 ÷ - j6 = - 5
Números Complexos em Eletrônica – Prof. Edgar Zuim
e) - j30 ÷ - j5 = 6
f) - j15 ÷ - j3 = 5
Página 4
IV- MULTIPLICAÇÃO DE UM NÚMERO IMAGINÁRIO POR UM NÚMERO
IMAGINÁRIO ( multiplicação de um termo j por um termo j )
Multiplica-se o número e o operador j. A multiplicação dos termos j produzirá j2. Veja os
exemplos abaixo:
a) j3 . j4 = j . j = j2 = j2(3 . 4) = -1(12) = -12
b) j3 . - j4 = j . - j = - j2(3 . 4) = -(-1)(12) = 12
V - MULTIPLICAÇÃO DE NÚMEROS COMPLEXOS
Basta seguir as regras da álgebra (propriedade distributiva), conforme mostra o exemplo
abaixo:
a) (9 + j5) . (3 - j2)
= 27 + j15 - j18 - j210  observe que j2 = -1
= 27 - j3 + 10
= 37 - j3
VI - DIVISÃO DE NÚMEROS COMPLEXOS
A divisão de um número real por um número complexo não é possível.
Consideremos a expressão:
4 - j1
1 + j2
O numerador contém um número real, que é 4 e o denominador é formado por um número
complexo: 1 + j2, tornando impossível a operação.
Para concretizar a operação torna-se necessário racionalizá-la, bastando para isso multiplicar
o numerador e o denominador pelo conjugado do denominador.
O conjugado do denominador é 1 - j2 (basta trocar o sinal).
Teremos então:
(4 - j1) . (1 - j 2)
(1 + j 2) . (1 - j 2)

4 - j9 - 2
2 - j9
4 - j8 - j1 + j 2 2
=
=
= 0,4 - j1,8
2
1+ 4
5
1- j 4
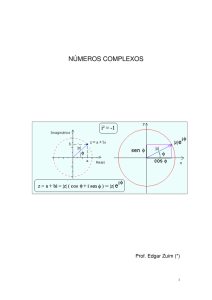
MAGNITUDE E ÂNGULO DE UM NÚMERO COMPLEXO
“REPRESENTAÇÃO POLAR E RETANGULAR DE UM NÚMERO COMPLEXO
CONVERSÕES RETANGULAR/POLAR - POLAR/RETANGULAR”
Números Complexos em Eletrônica – Prof. Edgar Zuim
Página 5
Veja a figura abaixo:
Em termos elétricos, uma impedância complexa 4 + j3 significa 4Ω de resistência elétrica e
3Ω de reatância indutiva. Lembrar que, a impedância 4 + j3 está escrita na forma retangular.
A impedância é o resultado de: Z =
R 2 + XL
4 2 + 32 =
Z=
2
ou Z2 = R2 + XL2
16 + 9 =
25 = 5Ω
O ângulo de fase θ é o arco tangente (arctan) da relação entre XL e R.
Portanto: θ = arctan
XL
3
=
= 0,75 ≅ 37º
4
R
Desta forma, a impedância complexa pode ser escrita da seguinte maneira:
4 + j3Ω - forma retangular
- forma polar
EXERCÍCIOS RESOLVIDOS
Converter para a forma polar:
a) 2 + j4
=
22 + 42 =
4 + 16 =
20 = 4,47  arctan
4
= 2 ≅ 63º 
2
b) 8 + j6
=
64 + 36 =
100 = 10  arctan
6
= 0,75 ≅ 37º 
8
32 = 5,66  arctan
-4
= -1 = - 45º 
4
c) 4 - j4
= 16 + 16 =
Números Complexos em Eletrônica – Prof. Edgar Zuim
Página 6
Converter para a forma retangular:
a)
sen 65º = 0,906 (parte imaginária)  12 . 0,906 = 10,87
cos 65º = 0,423 (parte real)  12 . 0,423 = 5,08
Resposta: 5,08 + j10,87
b)
sen 60º = 0,866 (parte imaginária)  100 . 0,866 = 86,6
cos 60º = 0,5 (parte real)  100 . 0,5 = 50
Resposta: 50 + j86,6
c)
sen - 60º = - 0,866 (parte imaginária)  100 . - 0,866 = - 86,6
cos - 60º = 0,5 (parte real)  100 . 0,5 = 50
Resposta: 50 - j86,6
d)
sen 90º = 1 (parte imaginária)  10 . 1 = 10
cos 90º = 0 (parte real)  10 . 0 = 0
Resposta: 0 + j10
Quando um número complexo é formado por uma parte real igual a zero, como por exemplo:
0 + j5, a expressão na forma polar será:
Para a expressão: 0 - j5, a expressão na forma polar será:
Quando um número complexo é formado por uma parte imaginária igual a zero, como por
exemplo: 5 + j0, a expressão na forma polar será:
MULTIPLICAÇÃO DE NÚMEROS COMPLEXOS NA FORMA POLAR
I - REAL x POLAR
a)
Números Complexos em Eletrônica – Prof. Edgar Zuim
Página 7
b)
II - POLAR x POLAR
Na multiplicação de números complexos (polar x polar) os ângulos são somados
algebricamente, conforme mostra os exemplos abaixo:
a)
b)
c)
DIVISÃO DE NÚMEROS COMPLEXOS NA FORMA POLAR
I - POLAR ÷ REAL
a)
b)
c)
II - POLAR ÷ POLAR
Na divisão de números complexos na forma polar (polar ÷ polar) os ângulos são subtraídos
algebricamente, conforme mostra os exemplos a seguir:
a)
b)
c)
III - REAL ÷ POLAR
a)
b)
Números Complexos em Eletrônica – Prof. Edgar Zuim
Página 8
EXERCÍCIOS RESOLVIDOS UTILIZANDO NÚMEROS COMPLEXOS
I - Dado o circuito abaixo:
Calcule as correntes I1, I2 e I3; as impedâncias Z1; Z2 e Z3; a corrente total (IT) e a impedância
total (ZT) nas formas retangular e polar.
Solução:
1) escrevendo cada ramo de impedância na forma retangular, temos:
Z1 = 50 - j50Ω
Z2 = 40 + j30Ω
Z3 = 30 + (j110 - j70) = 30 + j40Ω
2) convertendo cada ramo de impedância na forma polar, temos:
- 50
= -1 = - 45º 
50
Z1 =
50 2 + (-50) 2 = 70,7  θ = arctan
Z2 =
40 2 + 30 2 = 50  θ = arctan
30
= 0,75 = 36,87º (37º) 
40
Z3 =
30 2 + 40 2 = 50  θ = arctan
40
= 1,33 = 53,15º (53º) 
30
3) Calculando a corrente em cada ramo de impedância, ou seja, as correntes I1, I2 e I3:
I1 = Vin / Z1
 1 + j1A (retangular)
I2 = Vin / Z2
 1,6 - j1,2A (retangular)
I3 = Vin / Z3
Números Complexos em Eletrônica – Prof. Edgar Zuim
Página 9
 1,2 - j1,6A (retangular)
4) Calculando a corrente total (forma retangular):
IT = I1 + I2 + I3 = 1 + 1,6 + 1,2 + j1 - j1,2 - j1,6
IT = 3,8 - j1,8A
convertendo para a forma polar:
IT =
3,8 2 + (-1,8) 2 = 4,2  θ = arctan
1,8
= - 0,474 = - 25.4º 
- 3,8
5) Calculando a impedância total (forma polar):
ZT = Vin / IT
Convertendo para a forma retangular:
23,8 . sen 25,4º = 23,8 . 0,429 = 10,21 (indutiva)
23,8 . cos 25,4º = 23,8 . 0,903 = 21,5 (resistiva)
ZT = 21,5 + j10,21Ω
II - Dado o circuito a seguir:
a) calcule as tensões em cada um dos componentes;
b) desenhe o fasor do circuito para a corrente e as tensões.
Solução:
1) Calculando a impedância total na forma retangular:
ZT = 2 + j4 + 4 - j12  6 - j8Ω
2) Convertendo a impedância total na forma polar:
Números Complexos em Eletrônica – Prof. Edgar Zuim
Página 10
ZT =
6 2 + (-8) 2 = 10  arctan
-8
= - 1,33 = -53,13º (- 53º)
6
ZT =
3) Calculando a corrente total na forma polar:
IT = VT / IT
4) Calculando a tensão em cada componente:
VR1 =
VL =
VC =
VR2 =
OBS: Como o operador j representa o ângulo de 90º, na forma polar a reatância indutiva (XL)
assume o ângulo de 90º ; a reatância capacitiva XC assume o ângulo - 90º e a resistência assume o
ângulo de 0º.
5) Desenhando o fasor do circuito para as tensões e a corrente, onde alguns aspectos devem ser
observados:
a) O ângulo de 53º para VR1 e VR2 mostra que as tensões nestes dois componentes estão em fase
com a corrente.
b) A tensão nos resistores está adiantada 53º em relação a VT enquanto que a tensão no capacitor está
atrasada 37º.
c) A tensão no indutor está adiantada 143º em relação a VT (90º + 53º).
d) A relação de fase entre as tensões no capacitor e indutor é de 180º.
Números Complexos em Eletrônica – Prof. Edgar Zuim
Página 11
6) Comprovando:
OBS: a soma das tensões de cada um dos componentes deverá nos dar a tensão aplicada na
entrada.
Convertendo cada tensão para a forma polar:
VR1 =
= 2,407 + j3,196V
VR2 =
= - 6,389 + j4,814V
VC =
= 19,167 - j14,444V
VL =
Total da VT
= 4,812 + j6,389V
= 19,997 + j0,045V
Convertendo a tensão 19,997 + j0,045V para a forma polar:
VT = 19,997 2 + 0,045 2 = 399,882 ≅ 20
0,045
= 0,00225 = 0,129º ≅ 0º
θ = arctan
19,997
Portanto, na forma polar VT =
Números Complexos em Eletrônica – Prof. Edgar Zuim
Página 12
FORMULÁRIO PARA CIRCUITOS AC
1 - ASSOCIAÇÃO DE INDUTORES
EM SÉRIE: LT = L1 + L2 + L3 + L4 …
EM PARALELO:
1
1
1
1
1
=
+
+
+
… (para mais de dois indutores)
L1
L3
L4
LT
L2
ou
L1 . L 2
LT =
(para dois indutores)
L1 + L 2
2 - ASSOCIAÇÃO DE CAPACITORES
EM SÉRIE:
1
1
1
1
1
=
+
+
+
… (para mais de dois capacitores)
CT
C4
C1
C2
C3
ou
C .C
CT = 1 2 (para dois capacitores)
C1 + C 2
EM PARALELO: CT = C1 + C2 + C3 + C4 …
3 - CIRCUITO RC EM SÉRIE
VR = R.IT
VT =
VR + VC
2
θ = arctan Z=
R 2 + XC
2
Z=
VT
IT
Números Complexos em Eletrônica – Prof. Edgar Zuim
2
VC = XC . IT
VC
X
= - C
VR
R
IT =
VT
Z
Página 13
XC =
1
, onde ω = 2 π f
ωC

XC =
1
2π f C
f = frequência em hertz
C = capacitância em farads
Fasor representando a impedância total ( Z ) de um circuito RC série.
A defasagem entre R e XC é de 90º.
4 - CIRCUITO RC EM PARALELO
IT =
IR + IC
2
2
IR =
VT
R
θ = arctan
IT =
VT
Z
IC =
VT
XC
IC
IR
Z=
VT
IT
5 - CIRCUITO RL EM SÉRIE
VT =
VR + VL
2
2
VR = R . IT
Números Complexos em Eletrônica – Prof. Edgar Zuim
VL = XL . IT
Página 14
θ = arctan
VL
X
= L
VR
R
XL = ω L , onde ω = 2 π f

XL = 2 π f L
f = frequência em hertz
L = indutância em henry
Fasor representando a impedância total ( Z ) de um circuito RL série.
A defasagem entre R e XL é de 90º.
Z=
R 2 + XL
2
Z=
VT
IT
IT =
VT
Z
6 - CIRCUITO RL EM PARALELO
IT =
IR + IL
2
2
Z=
VT
IT
θ = arctan -
Números Complexos em Eletrônica – Prof. Edgar Zuim
IT =
VT
Z
IL
IR
Página 15
1  1
  + 
 R   XL
2
Z=
R . XL
R 2 + XL

2
Z=
1  1
  + 
 R   XL
2






2
2
7 - CIRCUITO LC EM SÉRIE
2
Z=
XL - XC
2
XL - XC = X
XC - XL = X
logo: Z = X
Z=
VT
IT
IT =
VT
Z
8 - CIRCUITO LC EM PARALELO
Z=
X L . (-X C )
X L + (-X C )
- Z  capacitiva
Z  indutiva
IT =
2
I L + I C , onde: IL =
2
Z=
VT
IT
VT
V
e IC = T
XL
XC
IT =
VT
Z
9 - CIRCUITO RLC EM SÉRIE
Números Complexos em Eletrônica – Prof. Edgar Zuim
Página 16
R 2 + X2
Z=
onde:
X = XL - XC ou
X = XC - XL
O fasor para o circuito acima é mostrado a seguir.
Observe que a defasagem entre as tensões do capacitor e do indutor é de 180º, no entanto,
entre estes componentes e o resistor é de 90º.
VL = XL . IT
VC = XC . IT
VR = R . IT
VT = VR + VX
onde:
VX = VL - VC ou
VX = VC - VL
2
Z=
2
VT
V
 IT = T
IT
Z
Números Complexos em Eletrônica – Prof. Edgar Zuim
Página 17
VL - VC
V
= X  ( VL > VC )
VR
VR
V - VL
V
θ = arctan - C
= - X  ( VC > VL )
VR
VR
θ = arctan
XL - XC
X
( XL > XC ) = arctan
R
R
X - XL
X
θ = arctan - C
( XC > XL ) = R
R
θ = arctan
10 - CIRCUITO RLC EM PARALELO
VT
XL
V
IC = T
XC
V
IR = T
R
IL =
IR + IX
2
IT =
2
onde:
IX = IL - IC ou
IX = IC - IL
O fasor de um circuito RLC em paralelo é mostrado abaixo, onde prevalecem as correntes IC ,
IL e IR.
θ = arctan -
θ = arctan
IL - IC
I
= - X ( IL > IC )
IR
IR
IC - IL
I
= X ( IC > IL )
IR
IR
Números Complexos em Eletrônica – Prof. Edgar Zuim
Página 18
Calculando a impedância em um circuito paralelo:
x.y
Z=
x=
x 2 + y2
onde:
X L . (- X C )
X L + (-X C )
y=R
A impedância de um circuito RLC paralelo pode também ser calculada pela fórmula:
1
 1   1
  +
 R   XC XL
2
Z=
Z =
1
 1   1
  +
 R   XC XL
2
VT
IT






2
2
IT =
Podemos também calcular θ com as fórmulas: θ = arctan

VT
Z
R
Z
e θ = arccos
X
R
11 - POTÊNCIA EM CIRCUITOS AC
Em circuitos AC existem três potências distintas: real, reativa e aparente identificadas
respectivamente pelas letras P ( W ), Q ( VAR ) e S ( VA ).
P = V . I . cosθ = VR . I = R . I2 (potência real = W)
Q = V . I . senθ ( potência reativa = VAR)
S = V . I (potência aparente = VA)
CIRCUITO INDUTIVO:
Números Complexos em Eletrônica – Prof. Edgar Zuim
Página 19
P = VI cosθ
Q = VI senθ
S = VI
cos 90º = 0
sen 90º = 1
∴Q = S (não há potência real)
CIRCUITO CAPACITIVO:
P = VI cosθ
Q = VI senθ
S = VI
cos 90º = 0
sen 90º = 1
∴Q = S (não há potência real)
CONCLUSÃO: Em um capacitor ou indutor a potência reativa é igual a potência
aparente.
Q = S  VAR = VA 
P =0
12 - FATOR DE POTÊNCIA
Fp =
VI . cosθ
VI
Fp = cosθ
Fp =
Potência real
Potência aparente
θ = arctan
Fp =
Q
P
P
S
Q = P . tanθ
Fator de potência indutivo: motores de indução, indutores, etc.
Fator de potência capacitivo: motores síncronos, banco de capacitores, etc.
Fator de potência para circuitos paralelos: Fp = arccos
Fator de potência para circuitos série: Fp = arccos
IR
IT
R
Z
RELAÇÕES ENTRE TENSÃO E CORRENTE NUM CIRCUITO AC
INDUTIVO
Numa indutância:
a) a tensão aplicada está adiantada 90º em relação à corrente;
b) a FCEM (força contra eletromotriz) está atrasada 90º em relação à corrente;
c) a tensão aplicada à entrada e a FCEM estão 180º defasadas.
Números Complexos em Eletrônica – Prof. Edgar Zuim
Página 20
CONCLUSÃO: Qualquer circuito AC que contenha apenas indutância apresenta três variáveis
importantes: a) tensão aplicada; b) força contra eletromotriz induzida e c) corrente do circuito.
FCEM: é a voltagem contrária originada num circuito indutivo pela passagem de uma corrente
alternada ou pulsativa.
LEI DE LENZ: uma fem (força eletromotriz) produzida pela indução tende a estabelecer uma
corrente cujo sentido opõe-se ao campo primitivo que a produziu.
RELAÇÕES ENTRE TENSÃO E CORRENTE NUM CIRCUITO AC
CAPACITIVO
A corrente através do capacitor está adiantada em relação à tensão aplicada ao capacitor de
90º.
Conforme ilustra a figura abaixo, a corrente através do capacitor está defasada de 90º tanto
em relação à tensão aplicada como em relação à contra-tensão.
Portanto, a corrente está adiantada de 90º em relação à tensão aplicada e atrasada de 90º em
relação à contra-tensão.
EFEITOS DA CONTRA-TENSÃO:
•
Quando uma fonte de tensão DC é ligada nos extremos de um capacitor, a corrente é máxima
quando a tensão da fonte, senoidalmente, começa a crescer a partir do zero, desde que as placas
do capacitor estejam neutras (sem carga) e não apresentem forças eletrostáticas opostas.
Números Complexos em Eletrônica – Prof. Edgar Zuim
Página 21
•
Quando a tensão da fonte cresce, as cargas nas placas do capacitor que resultam do fluxo de
corrente, aumentam.
•
À medida que a carga no capacitor aumenta, resulta numa tensão que se opõe à tensão aplicada,
resultando numa diminuição da corrente.
•
Quando a tensão da fonte (tensão aplicada) atinge o valor máximo ou valor de pico, o capacitor
estará com a máxima carga e máxima tensão apresentando assim uma oposição à tensão aplicada
(cargas eletrostáticas opostas), as quais se anulam, resultando então em uma corrente zero.
•
Quando a tensão aplicada nos extremos do capacitor começa a decrescer, a carga eletrostática nas
placas do capacitor torna-se maior do que o potencial dos terminais da fonte e o capacitor começa
a descarregar-se, repetindo assim o processo, porém no sentido inverso.
Números Complexos em Eletrônica – Prof. Edgar Zuim
Página 22