Quadrilatero james - Colégio MilleniumClasse

COLÉGIO MILLENIUM CLASSE
QUADRILÁTEROS – FRENTE B – 1° ANO – PROF. JAMES
Quadrilátero
Soma das medidas dos ângulos internos de um quadrilátero convexo
A soma do ângulos internos de um quadrilátero convexo é 360º.
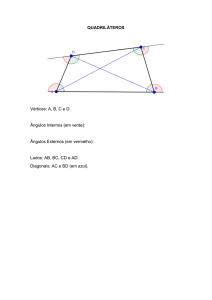
Podemos provar tal afirmação decompondo o quadrilátero ABCD nos triângulos ABD e BCD.
Do triângulo ABD, temos : a + b1 + d1 = 180º. (1)
Do triângulo BCD, temos: c + b2 + d2 = 180º.
(2)
Adicionando(1) com (2) , obtemos:
a + b1 + d1 + c + b2 + d2 = 180º + 180º
a + b1 + d1 + c + b2 + d2 = 360º
a + b + c + d = 360º
Observações
1.Termos uma fórmula geral para determinação da soma dos ângulos internos de qualquer
polígono convexo:
Si = (n - 2)·180º, onde n é o número de lados do polígono.
2. A soma dos ângulos externos de um polígono convexo qualquer é 360º.
Se = 360º
Quadriláteros Notáveis
Paralelogramo
Paralelogramo é o quadrilátero que tem os lados opostos paralelos.
Exemplo:
h é a altura do paralelogramo.
O ponto de intersecção das diagonais (E) é chamado centro de simetria.
Destacamos alguns paralelogramos:
Retângulo
Retângulo é o paralelogramo em que os quatro ângulos são congruentes
(retos).
Exemplo:
Losango
Losango é o paralelogramo em que os quatro lados são congruentes.
Exemplo:
Quadrado
Quadrado é o paralelogramo em que os quatro lados e
os quatro ângulos são congruentes.
Exemplo:
É o único quadrilátero regular. É, simultaneamente
retângulo e losango.
Trapézio
É o quadrilátero que apresenta somente dois lados paralelos
chamados bases.
Exemplo:
Denominamos trapezóide o quadrilátero que não apresenta lados paralelos.
Destacamos alguns trapézios:
Trapézio retângulo
É aquele que apresenta dois ângulos retos.
Exemplo:
Trapézio isósceles
É aquele em que os lados não-paralelos são congruentes.
Exemplo:
Trapézio escaleno
É aquele em que os lados não-paralelos não são congruentes.
Exemplo:
Propriedades dos Paralelogramos
1ª Propriedade
Os lados opostos de um paralelogramo são congruentes.
H: ABCD é paralelogramo.
T:
Demonstração
Afirmativa
Justificativa
1.
Segmentos de paralelas entre paralelas.
2.
Segmentos de paralelas entre paralelas.
2ª Propriedade
Cada diagonal do paralelogramo o divide em dois triângulos
congruentes.
H: ABCD é paralelogramo.
T:
Demonstração
Afirmativa
Justificativa
1.
Hipótese.
2.
Hipótese.
3.
Lado comum.
4.
Caso L.L.L.
3ª Propriedade
As diagonais de um paralelogramo interceptam-se mutuamente ao meio.
H: ABCD é paralelogramo
T:
Demonstração
Afirmativa
Justificativa
1.
2.
3.
é diagonal (2ª propriedade)
Ângulos correspondentes em triângulos
congruentes.
Ângulos correspondentes em triângulos
congruentes.
4.
5.
4ª Propriedade
As diagonais de um paralelogramo interceptam-se mutuamente ao meio.
H: ABCD é paralelogramo.
T:
Demonstração
Afirmativa
Justificativa
1.
Ângulos alternos internos.
2.
Lados opostos (1ª propriedade).
3.
Ângulos alternos internos.
4.
Caso A.L.A..
Lados correspondentes em triângulos
congruentes.
5.
Resumindo:
Num paralelogramo:
•
•
•
•
os lados opostos são congruentes;
cada diagonal o divide em dois triângulos congruentes;
os ângulos opostos são congruentes;
as diagonais interceptam-se em seu ponto médio.
Propriedade característica do retângulo.
As diagonais de um retângulo são congruentes.
T: ABCD é retângulo.
H:
.