LÍNGUA PORTUGUESA

Aluno(a):_____________________________________________________________ Código:__|__|__|__|__
Série: 1ª  Turma: _______
Data: ___/___/___
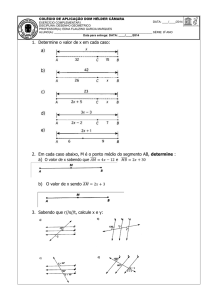
03. Determine x em cada caso:
01. Determine o número de diagonais dos seguintes polígonos:
a) hexágono
b) undecágono
c) icoságono
04. Sendo as figuras abaixo um triângulo e um pentágono regular,
determine x em cada item:
02. Determine o número de diagonais que não passam pelo centro dos
seguintes polígonos regulares:
a) decágono
b) pentadecágono
05. Um polígono regular possui a partir de um de seus vértices tantas
diagonais quantas são as diagonais de um hexágono. Determine:
a) o polígono;
c) dodecágono
2
Rua T-53 Qd. 92 Lt. 10/11 nº 1356 – Setor Bueno – 62-3285-7473 – www.milleniumclasse.com.br
b) o total de diagonais;
b) a medida do sétimo ângulo é.
c) a soma dos ângulos internos;
07. Sabendo que a figura abaixo nos mostra um mosaico onde todos os
pentágonos são regulares e iguais entre si, então determine:
a) o valor x + y.
d) a soma dos ângulos externos;
b) a soma dos ângulos internos de todos os pentágonos e quadriláteros
da figura.
e) a medida de cada ângulo interno e externo.
08. Em uma circunferência, há 96 pontos, igualmente espaçados,
marcados pelos números ímpares. Um polígono regular de 32 lados é
inscrito nessa circunferência e um de seus vértices é o ponto de número
1.
06. Seja o heptágono irregular, ilustrado na figura seguinte, onde seis de
seus ângulos internos medem 120º, 150º, 130º, 140º, 100º e 140º.
Determine:
a) a soma dos ângulos internos desse polígono;
a) o número de diagonais que não passam pelo centro desse polígono é?
3
Rua T-53 Qd. 92 Lt. 10/11 nº 1356 – Setor Bueno – 62-3285-7473 – www.milleniumclasse.com.br
b) A soma dos números de todos os vértices desse polígono é?
11. Numa comunidade constituída de 1.800 pessoas há três programas de
TV favoritos: Esporte (E), Novela (N) e Humorismo (H). A tabela abaixo
indica quantas pessoas assistem a esses programas.
Programas Nº de Telespectadores
E
400
N
1220
H
1080
EeN
220
NeH
800
EeH
180
E, N e H 100
Através desses dados, determine o número de pessoas da
comunidade que não assistem a qualquer dos três programas.
09. Os lados de um octógono regular são prolongados até que se obtenha
uma estrela.
a) faça um esboço dessa figura.
12. Uma população utiliza 3 marcas diferentes de detergente: A, B e C.
Feita uma pesquisa de mercado colheram-se os resultados tabelados
abaixo.
Marcas
Nº de Consumidores
A
109
B
203
C
162
AeB
25
AeC
28
BeC
41
A, B e C
5
Nenhum deles
115
b) A soma das medidas dos ângulos internos dos vértices dessa estrela é
Determine o número de pessoas que consomem ao menos duas marcas.
10. Pentágonos regulares congruentes podem ser conectados, lado a
lado, formando uma estrela de cinco pontas, conforme destacado na
figura. Nestas condições, o ângulo mede?
13. Num grupo de 50 esportistas, 25 jogam tênis, 29, basquete e 15
praticam os dois esportes. Sabendo-se que x esportistas do grupo não
jogam tênis ou basquete, determine o valor de x.
4
Rua T-53 Qd. 92 Lt. 10/11 nº 1356 – Setor Bueno – 62-3285-7473 – www.milleniumclasse.com.br
14. Dos 80 alunos de uma turma, 15 foram reprovados em Matemática,
11 em Física e 10 em Química. Oito alunos foram reprovados
simultaneamente em Matemática e Física, seis em Matemática e Química
e quatro em Física e Química. Sabendo que 3 alunos foram reprovados
nas três disciplinas, determine quantos alunos não foram reprovados em
nenhuma dessas disciplinas.
18. Dados os conjuntos A = {a, b, c}, B = {b, c, d} e C = {a, c, d, e},
determine o conjunto (A – C)  (C – B)  (A  B  C).
15. Dados os conjuntos A = {a, b, c}, B = {a, c, e, g} e C = {a, b, d, f},
determine o número de elementos do conjunto (A  B) U (C – B).
19. Se n é o número de subconjuntos não vazios do conjunto formado
pelos múltiplos estritamente positivos de 5, menores do que 40, calcule o
valor de n.
16. Sabendo-se que A e B são subconjuntos de U, A  B = {c, d} A  B =
{a, b, c, d, e, f} e CUA = {e, f, g, h, i}, determine n(A) e n(B).
20. Considere três conjuntos A, B e C, tais que: na = 28, nb = 21, nc = 20,
n(A  B) = 8, n(B  C) = 9, n(A  C) = 4 e n(A  B  C) = 3. Assim sendo,
determine o valor de n((A  B)  C).
17. Se A = {1}, B = {0, 1} e E = {0, 1, 2} , determine o conjunto C(EA  B) .
5
Rua T-53 Qd. 92 Lt. 10/11 nº 1356 – Setor Bueno – 62-3285-7473 – www.milleniumclasse.com.br