(An) = (det A)

Determinantes
Propriedades dos determinantes
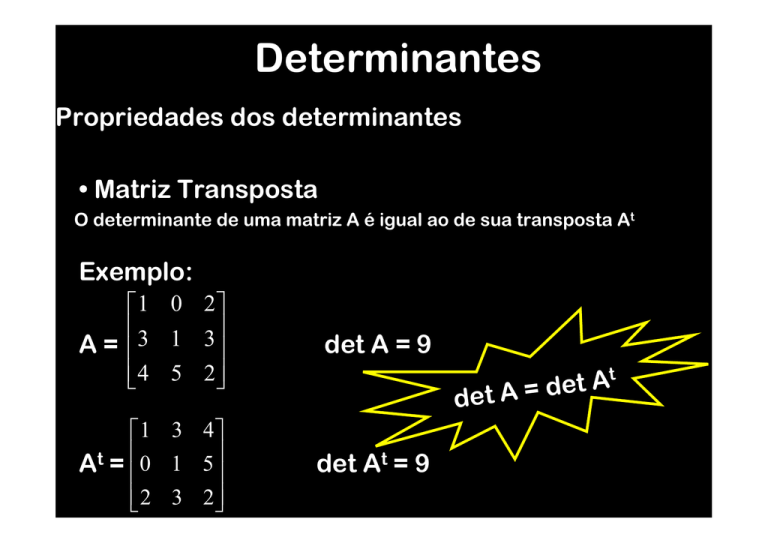
• Matriz Transposta
O determinante de uma matriz A é igual ao de sua transposta At
Exemplo:
1 0 2
3 1 3
A= 

 4 5 2 
det A = 9
d
1 3 4 
At =  0 1 5 
 2 3 2 
det At = 9
t
A
t
e
et A = d
Determinantes
Propriedades dos determinantes
• Matriz triangular
É aquela cujos os elementos situados “de um mesmo lado” da diagonal
principal são iguais a zero.
Seu determinante é o produto dos elementos da diagonal principal
Exemplo:
 a11
3
A= 
 4
0
a22
5
0
0 
a33 
det A = a11 . a22 . a33
Determinantes
Propriedades dos determinantes
• Matriz de Vandermonde (ou das potências)
São aquelas onde as colunas de uma matriz M, de ordem n, sã formadas por
potências de mesma base, cm expoente inteiro, variando desde 0 até n (os elementos de cada coluna formam uma progressão geométrica cujo
primeiro elemento é 1.
Exemplo:
1 1 1 
A =  2 3 4 
 4 9 16 
Elementos característicos da matriz
det A = (4-3).(4-2).(3-2) = 2
Determinantes
Propriedades dos determinantes
• Troca de filas paralelas
Se B é uma matriz que se obtém de uma matriz quadrada A, quando
trocamos entre si a posição de duas filas paralelas, então
Exemplo:
1 0 2
3 1 3
A= 

 4 5 2 
det A = 9
4 5 2
B =  3 1 3 
1 0 2 
det B = - 9
A
t
e
d
=
det B
Determinantes
Propriedades dos determinantes
• Filas paralelas iguais
Se uma matriz A possui duas filas paralelas (duas linhas ou duas colunas)
Formadas por elementos respectivamente iguais, então det A = 0
Exemplo:
A=
 0

 2
 −5

 0
 2

1
4
0
1
0
−1

25 −54 13 
−14 0 −3

3
5 −1
35
0
41
3
5
det A = 0
Determinantes
Propriedades dos determinantes
• Multiplicação de uma fila por uma constante
Se B é uma matriz que obtemos de uma matriz quadrada A, quando
multiplicamos uma de suas filas( linha ou coluna) por uma constante k,
Então:
det B = k.det A
Exemplo:
A=
1 0 2
3 1 3


 4 5 2 
det A = 9
B=
1 0 2
9 3 9 


 4 5 2 
det B = 27
det B = 3.det A
Determinantes
Propriedades dos determinantes
• Multiplicação de uma fila por uma constante
Exemplo:
A=
1 0 2
3 1 3


 4 5 2 
det A = 9
B=
 3 0 6
 9 3 9


12 15 6 
det B = kn.det A
det B = 243
det B = 3.3.3.det A = det B = 33.det A
Determinantes
Propriedades dos determinantes
• Fila Nula
Se os elementos de uma fila qualquer (linha ou coluna) de uma
matriz M de ordem n forem todos nulos, então det M = 0
Exemplo:
A
0 0 0
=  3 1 3
 4 5 2 
det A = 0
Determinantes
Propriedades dos determinantes
• Adição de determinantes
Se A, B e C são matrizes quadradas de mesma ordem, tais que os elementos
correspondentes de A, B e C são iguais entre si, exceto os de uma fila, em que os
elementos de C são iguais às somas dos seus elementos correspondentes de A
então:
det A + det B = det C
Exemplo:
A=
a r
b s

 c t
d
e 
f 
a u
B= b v
 c x
d
e 
f 
C=
a r + u
b s + v

 c t + x
d
e 
f 
Determinantes
Propriedades dos determinantes
• Teorema de Jacobi
O determinante não se altera quando adicionamos uma fila qualquer com outra
fila paralela multiplicada por um número.
Exemplo:
A=
a
d

 g
b
e
h
c
f 
i 
a
B=  d
 g
b
e
h
c + ma 
f + md 
i + mg 
B
t
e
d
=
A
det
Determinantes
Propriedades dos determinantes
• Teorema de Binet
Sendo A e B matrizes quadradas de mesma ordem, então:
det (A · B) = det A · det B.
det (A.B) = det A.det B
Exemplo:
A=
1 0 2
3 1 3


 4 5 2 
det A = 9
B=
1 0 2
9 3 9 


 4 5 2 
det B = 27
det (A.B) = 9 . 27 = 243
Determinantes
Propriedades dos determinantes
• Teorema de Binet
Conseqüências:
det (An) = (det A)n
det (A-1) = 1
det A
Só existe matriz inversa
se det A ≠ 0
Determinantes
Propriedades dos determinantes
• Teorema da combinação linear
Se uma matriz quadrada M, de ordem n, tem uma linha (ou coluna
Que é combinação linear de outras linhas (ou colunas), então:
det (M) = 0
Exemplo:
A=
 2 3 5
 4 −1 3 


 5 4 9 
3º coluna = 1. 1ºcoluna + 1 . 2º coluna
5 = 1. 2 + 1 . 3