Cinemática dos Fluidos

UNIVERSIDADE DE SÃO PAULO
ESCOLA DE ENGENHARIA DE SÃO CARLOS
Núcleo de Engenharia Térmica e Fluidos
Mecânica dos Fluidos (SEM5749) – Prof. Oscar M.H. Rodriguez
Cinemática dos Fluidos
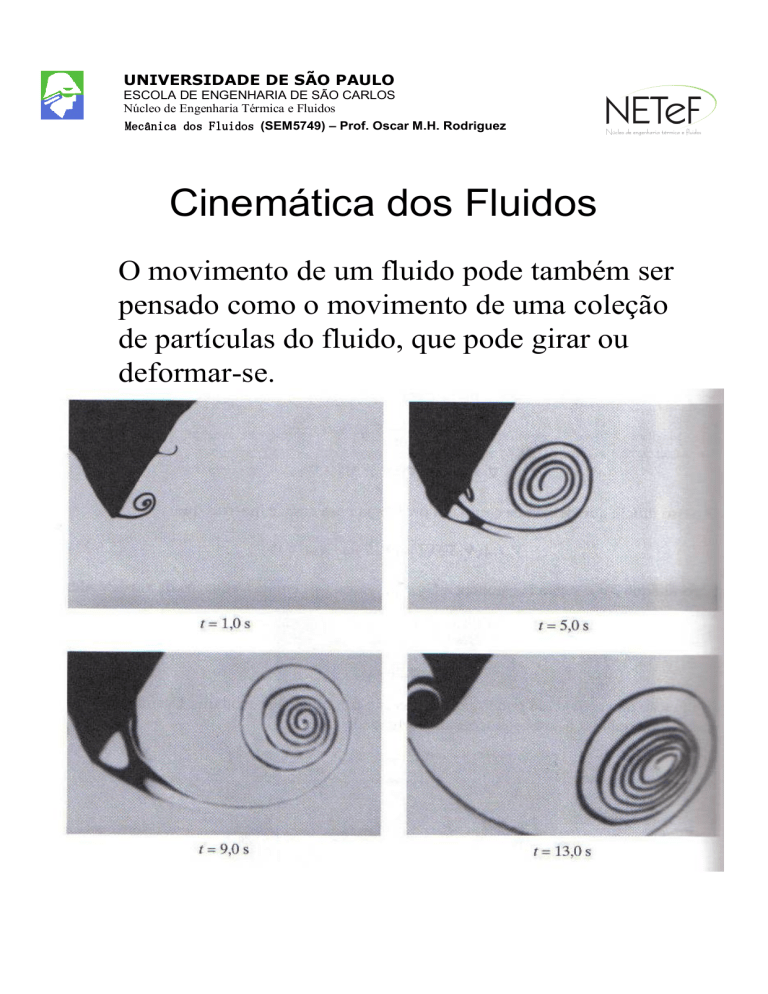
O movimento de um fluido pode também ser
pensado como o movimento de uma coleção
de partículas do fluido, que pode girar ou
deformar-se.
UNIVERSIDADE DE SÃO PAULO
ESCOLA DE ENGENHARIA DE SÃO CARLOS
Núcleo de Engenharia Térmica e Fluidos
Mecânica dos Fluidos (SEM5749) – Prof. Oscar M.H. Rodriguez
Componentes dos movimentos dos fluidos
UNIVERSIDADE DE SÃO PAULO
ESCOLA DE ENGENHARIA DE SÃO CARLOS
Núcleo de Engenharia Térmica e Fluidos
Mecânica dos Fluidos (SEM5749) – Prof. Oscar M.H. Rodriguez
1. Campo de aceleração de uma partícula de fluido
ap =
DV
Dt
,
aceleração total
de uma partícula
∂V
∂V
∂V
∂V
=u
+v
+w
+
∂x
∂y
∂z
∂t
,
aceleração
local
aceleração convectiva
• A expressão acima descreve a aceleração de uma
partícula em qq. lugar no campo de escoamento V = V
(x,y,z,t); este é o método euleriano de descrição.
• V = V (x,y,z,t) é a variável mais importante da
mecânica dos fluidos; conhecer o campo vetorial da
velocidade é praticamente equivalente a resolver um
problema de escoamento de um fluido
Pgm1 (10:05)
ˆj m/s
DE SÃO PAULO
V = 2 x î + 2 y UNIVERSIDADE
ESCOLA DE ENGENHARIA DE SÃO CARLOS
Núcleo de Engenharia Térmica e Fluidos
Mecânica dos Fluidos (SEM5749) – Prof. Oscar M.H. Rodriguez
Exemplo 1:
a) Encontre o campo vetorial da aceleração para o
escoamento de um fluido que tem o seguinte campo de
velocidade, em que x, y e z são dados em metros:
V = 2 x î + 2 y ˆj m/s
b) Calcule a aceleração no ponto (2, -1, 3).
UNIVERSIDADE DE SÃO PAULO
ESCOLA DE ENGENHARIA DE SÃO CARLOS
Núcleo de Engenharia Térmica e Fluidos
Mecânica dos Fluidos (SEM5749) – Prof. Oscar M.H. Rodriguez
2. Dilatação ou Deformação Linear
UNIVERSIDADE DE SÃO PAULO
ESCOLA DE ENGENHARIA DE SÃO CARLOS
Núcleo de Engenharia Térmica e Fluidos
Mecânica dos Fluidos (SEM5749) – Prof. Oscar M.H. Rodriguez
Durante a dilatação, a forma do elemento de
fluido permanece imutável, pois todos os ângulos retos
são mantidos. O elemento vai variar seu comprimento
na direção x somente se ∂u ∂x é diferente de zero
(analogamente para y e z).
A taxa de dilatação volumétrica local instantânea é
dado por:
∂u ∂v ∂w
Taxa de dilatação volumétrica =
+ +
= ∇ ⋅V
∂x ∂y ∂z
Para fluidos incompressíveis, a taxa de dilatação
volumétrica é zero
∇ ⋅V = 0
UNIVERSIDADE DE SÃO PAULO
ESCOLA DE ENGENHARIA DE SÃO CARLOS
Núcleo de Engenharia Térmica e Fluidos
Mecânica dos Fluidos (SEM5749) – Prof. Oscar M.H. Rodriguez
Exemplo 2: o seguinte campo de escoamento representa
um caso de possível escoamento incompressível?
V = 2 x î − 2 y ˆj m/s
UNIVERSIDADE DE SÃO PAULO
ESCOLA DE ENGENHARIA DE SÃO CARLOS
Núcleo de Engenharia Térmica e Fluidos
Mecânica dos Fluidos (SEM5749) – Prof. Oscar M.H. Rodriguez
3. Deformação
UNIVERSIDADE DE SÃO PAULO
ESCOLA DE ENGENHARIA DE SÃO CARLOS
Núcleo de Engenharia Térmica e Fluidos
Mecânica dos Fluidos (SEM5749) – Prof. Oscar M.H. Rodriguez
4. Rotação
γxy
γyx
UNIVERSIDADE DE SÃO PAULO
ESCOLA DE ENGENHARIA DE SÃO CARLOS
Núcleo de Engenharia Térmica e Fluidos
Mecânica dos Fluidos (SEM5749) – Prof. Oscar M.H. Rodriguez
Vorticidade
Assim:
w = iˆw x + ˆjw y + kˆw z =
1  ˆ ∂w ∂v  ˆ  ∂u ∂w  ˆ ∂v ∂u  
= i 
−  + j  −
 + k  −  
2   ∂y ∂z   ∂z ∂x   ∂x ∂y  
rotV =∇×V
ou:
1
w = ∇ ×V
2
Obs.:
1. O desenvolvimento de rotação em uma partícula
fluida requer a ação de uma tensão cisalhante na superfície
da mesma. A presença de forças viscosas significa que o
escoamento é rotacional.
2. A condição de irrotacionalidade
∇ ×V = 0
é uma hipótese válida para aquelas regiões do escoamento
nas quais as forças viscosas são desprezíveis
Finalmente, temos que o dobro da rotação é a vorticidade,
a qual é uma medida da rotação de um elemento de fluido
ζ = 2w = ∇ ×V
Pgm2 (07:00)
UNIVERSIDADE DE SÃO PAULO
ESCOLA DE ENGENHARIA DE SÃO CARLOS
Núcleo de Engenharia Térmica e Fluidos
Mecânica dos Fluidos (SEM5749) – Prof. Oscar M.H. Rodriguez
Exemplo 3: Calcule a taxa de rotação para um elemento
de fluido onde o campo de velocidade é dado por:
Vr = 0, Vθ = k / r
(onde k é uma constante).
Este escoamento é rotacional ou irrotacional?
Pgm2 (07:00)