Document

Material sujeito a correções
ÍNDICE
1
ERROS NAS APROXIMAÇÕES NUMÉRICAS.....................................2
1.1
1.2
1.3
1.4
1.5
1.6
1.7
1.8
1.9
2
MATRIZES .....................................................................................12
2.1
2.2
2.3
2.4
2.5
2.6
3
4
Erros Absolutos ................................................................................................ 3
Erros Relativos ................................................................................................. 4
Erro de Arredondamento................................................................................... 5
Ordem decimal de um algarismo: ...................................................................... 5
Algarismos significativos corretos....................................................................... 5
Cálculo dos erros absoluto e relativo:................................................................. 6
Erro de Truncamento ........................................................................................ 9
Seqüências – Convergências.............................................................................. 9
Propagação de erros ....................................................................................... 10
Propriedades dos Determinantes ..................................................................... 15
Menor Complementar ..................................................................................... 16
Complemento Algébrico de um elemento (COFATOR) ....................................... 16
Matriz Adjunta ................................................................................................ 17
Matriz Inversa ................................................................................................ 17
Cálculo do Determinante ................................................................................. 22
VALORES E VETORES CARACTERÍSTICOS ....................................24
SISTEMAS DE EQUAÇÕES LINEARES ............................................26
4.1
Métodos Diretos ou de Eliminação ................................................................... 26
4.1.1
Método de Gauss ..................................................................................... 26
4.1.2
Método de Gauss-Jordan .......................................................................... 31
4.1.3
Condensação Pivotal ................................................................................ 34
4.1.4
Refinamento da Solução ........................................................................... 37
4.1.5
Inversão de Matrizes ................................................................................ 40
5
SISTEMAS DE EQUAÇÕES LINEARES ............................................42
5.1
5.2
5.3
5.4
6
Métodos Iterativos .......................................................................................... 42
Método de Jacobi............................................................................................ 43
Método de Gauss-Siedel .................................................................................. 45
Estudo da Convergência.................................................................................. 46
Decomposição LU..........................................................................47
6.1
6.2
Teorema LU ................................................................................................... 47
Esquema prático para a decomposição LU........................................................ 49
Página 1 de 55
Material sujeito a correções
1 ERROS NAS APROXIMAÇÕES NUMÉRICAS
Causas:
•
Divisões Inexatas;
•
Números Irracionais;
•
Abandono de Casas Decimais e
•
Etc.
Este último aspecto é de particular interesse no caso de computadores digitais.
O processo de solução de um problema físico, através de métodos numéricos, pode ser
representado como se segue:
Figura 1
Nas fases de modelagem e resolução podem ocorrer erros.
Ex.: Erro na fase de modelagem:
A variação no comprimento de uma barra de metal sujeita a certa variação de temperatura
é dado por:
(
∆l = l 0 α .t + β .t 2
)
onde:
∆l → var iação do comprimento
l0 → comprimento inicial
t → temperatura
α e β → coeficientes de dilatação de cada material.
Exemplo: Calcular a variação no comprimento de uma barra sujeita a 10º C de variação e
que tenha:
l 0 = 1m
α = 0 ,001253 
 exp erimentais
β = 0 ,000068
Logo,
(
)
∆l = 1. 0 ,001253.10 + 0 ,000068.10 2 = 0 ,019330
Os valores de α e β foram obtidos experimentalmente com precisão de 10-6.
Página 2 de 55
Material sujeito a correções
Logo:
0,001252 < α < 0,001254
0,000067 < β < 0,000069
Então:
(
)
∆l < 1.(0 ,001254.10 + 0,000069.10 )
∆l > 1. 0,001252.10 + 0,000067.10 2
2
Logo:
0,019220 < ∆l < 0,019440
ou
∆l = 0 ,0193 ± 10−4
Então vemos que uma imprecisão na sexta casa decimal de α e β, implicou uma imprecisão
na quarta casa decimal de ∆l.
A precisão do resultado não é só função do modelo matemático, mas também dos dados
de entrada.
1.1
Erros Absolutos
Quando se substitui um valor a por outro aproximado a’ (a’≠
≠a), define-se como erro
absoluto:
∆ = a − a'
Normalmente como não conhecemos o valor de a, o erro absoluto é indeterminado.
Trabalhamos então com a cota superior ε do erro absoluto, isto é:
ε≥∆
Assim, podemos dizer que:
a'− a ≤ ε ou a' - ε ≤ a ≤ a'+ε
e que a’ é valor aproximado de a com erro absoluto não superior a ε.
Ex.: Se a = 3.876,373 e só desejamos a parte inteira a’, o erro absoluto é:
∆a = a' − a = 0 ,373 ( 3.876 − 3.876 ,373 )
Página 3 de 55
Material sujeito a correções
1.2
Erros Relativos
Chama-se erro relativo cometido sobre um valor a, quando este é aproximado por a’ ao
quociente positivo:
δ=
∆
a
Como normalmente o valor de a não é conhecido, e é próximo de a’, costuma-se calcular
também uma cota superior para o erro relativo tal que:
δ≤
ε
a'
Onde ε é uma adequada cota superior de erro absoluto.
A substituição de a por a’ no denominador é justificável se:
a ≅ a'
que é o caso normalmente encontrado na prática.
“Erro relativo tem por objetivo dar uma idéia ao grau de uma influência do erro, no valor
desejado”.
O erro absoluto não traduz nada, se não soubermos a ordem de grandeza do valor
calculado.
Ex.:
a = 3876,373
b = 1,373
Como vemos, o efeito da aproximação de b é muito maior do que de a.
Considerando o erro relativo, teremos uma melhor visão deste efeito.
Para a:
δa =
0,373
< 10 − 4
3876,376
Para b:
δb =
0 ,373
< 2.10 − 1
1,373
Página 4 de 55
Material sujeito a correções
1.3
Erro de Arredondamento
Diz-se que um valor foi arredondado na posição de ordem n, se todos os algarismos
significativos de ordem n + 1 em diante forem abandonados de forma que o algarismos de
ordem n é aumentado de uma unidade, se e somente se, o de ordem n+1 for superior a n.
O arredondamento é feito, por exemplo, em computadores digitais que trabalham com um
número “d” fixo de algarismos significativos.
Se por exemplo d = 5 e tivermos com um valor igual a: 2,73589 (algarismos significativos).
A diferença entre estes valores é o erro de Arredondamento.
Estes erros podem se propagar cumulativamente, podendo afetar o resultado final.
1.4
Ordem decimal de um algarismo:
Diz-se que a ordem decimal de um algarismo significativo ai de um número a é m, se o
resultado quando substituímos ai por 1 e todos os outros algarismos significativos por
zeros, é 10n.
Ex.: No número 2,718278, a ordem decimal do algarismo significativo de ordem 6 é -5,
pois:
0 ,000010
= 10− 5
1
Quando um número está representado na forma normalizada, a ordem decimal do
algarismo significativo de ordem i é (–i + t).
Forma Normalizada de um número é a sua representação:
0, a1, a2, a3,...ad . 10t
Onde d é o número de algarismos significativos e ai, i = (1, 2, ...,d) são os algarismos.
1.5
Algarismos significativos corretos
Diz-se que um algarismo significativo de ordem “n” (an) de uma aproximação a’ de um
número a, é algarismo significativo correto, se o erro absoluto de a’ for inferior a 0,5.10m,
onde m é a ordem decimal desse algarismo.
Com esta definição é possível afirmar que se o número a e sua aproximação a’ tem
algarismos significativos coincidindo a partir da esquerda até o de ordem i, então o número
de algarismos significativos corretos é pelo menos (i – 1).
De fato, com a ordem decimal do algarismo significativo de ordem i é –i + t, então, com
essa coincidência, o erro absoluto deve ser menor que 10-i+t (t se refere a forma
normalizada) e por isso menor do que 0,5.10-i+t-1, como exemplo temos as aproximações
2,5 e 2,4 de 2,0.
Página 5 de 55
Material sujeito a correções
Para ambas existe coincidência até o algarismo significativo de ordem 1, no entanto só a
segunda aproximação tem um algarismo correto.
Ex.:
1,9999 e 2,05
2
(0,666....)
. O algarismo 8 da aproximação não é correto pois:
A aproximação 0,668543 de 3
0,668543 – 0,666 = 0,00187633 > 0,5.10-3
O número 0,668543 só possui dois algarismos significativos corretos.
Ex.: Seja o número a = 0,000045045. Por um processo numérico foi determinado para o
mesmo valor a’ = 0,000045270.
Aplicando a definição concluímos que a’ só tem dois algarismos significativos corretos.
Passando para a forma normalizada vem,
a = 0,45045.10-4 e a’ = 0,45270.10-4
1.6
Cálculo dos erros absoluto e relativo:
Absoluto:
∆ = a − a' = 0,000000225 = 0,00225.10. −4
∆ < 0,5.10 − 2 .10 − 4
Relativo:
0,00225.10 −4
δ =
< 0,5.10 − 2
−4
0,45045.10
Se considerarmos o erro absoluto, da ordem de 10-6, podemos ter uma idéia errônea do
número de algarismos significativos. No entanto, com a apreciação do erro relativo,
podemos perceber porque sua precisão não vai além dos dois primeiros algarismos
significativos.
Teorema
Se o erro relativo da aproximação a’ de a for maior que 0,5x10-s, então a’ tem pelo menos
“s” algarismos significativos corretos.
Demonstração
Seja a =µ.10t, onde µ é a mantissa da forma normalizada de a.
Suponhamos que o algarismo significativo a’s correspondente a as na aproximação a’ não é
correto.
Página 6 de 55
Material sujeito a correções
Devemos ter então pela fórmula (A)
a' − a = ∆ > 0 ,5 x10 − s + t
Como
a = µ x10t < 10t , devemos ter:
δ =
a'− a
> 0,5 x10 − t
o que por hipótese é absurdo.
a
Então o algarismo significativo a’s é correto e, portanto, todos os de ordem inferior.
C.Q.D.
Regras a serem observadas:
1. Fixar o número “d” de algarismos significativos para o cálculo.
2. Se os dados iniciais têm mais que “d” algarismos significativos, arredondá-los na
posição do algarismo de ordem d; caso contrário preencher as posições restantes
com zero
3. As operações de adição e subtração deverão ser realizadas sempre com dois
números de cada vez. Antes de iniciá-la arredondar o número de menor valor
absoluto, de modo que a mais baixa ordem decimal deste último possa ser a mesma
do outro.
4. Efetuar as operações de multiplicação normalmente e arredondar o produto de
forma que ele passe a ter “d” algarismos significativos.
5. Efetuar as operações de divisão até que o quociente tenha “d” algarismos
significativos.
6. Potenciações com expoentes inteiros deverão ser realizadas como multiplicações de
números, dois a dois.
7. Valores irracionais como “π”, e valores de funções elementares como, “sen x”, “cos
x”, “ex”, etc., usados como dados, deverão ser tomados com “d” algarismos
corretos.
8. Potenciações com expoentes não inteiros deverão ser realizadas por meio de
logaritmos com “d” algarismos significativos.
EX.: Calcular o valor de:
2 + 1,5367 x 0 ,00337 − ( 0 ,201 )3
, retendo 3 algarismos
22 ,32 + π
significativos.
As operações na ordem em que devem ser efetuadas são:
0,2013
Página 7 de 55
Material sujeito a correções
•
•
multiplicamos inicialmente 0,201x0,201 = 0,040401, arredondamos o resultado para
0,0404
multiplicamos agora 0,0404x0,201 = 0,0081204, arredondamos para 0,00812
1,5367x0,00337
•
arredondamos inicialmente os fatores para: 1,54 e 0,00337
•
efetuamos: 1,54x0,00337 = 0,0051898
•
arredondamos o resultado para: 0,00519
•
extraindo a raiz quadrada vem: 1,41
2
2 + 1 ,5367 x 0 ,00337
•
arredondar o produto na ordem decimal -2 : (1,5367x0,00337 = 0,0051)
0,01
•
adicionar: 1,41 + 0,01 = 1,42
2 + 1 ,5367 x 0 ,00337 − 0 ,2013
•
arredondar a potência na ordem decimal -2:
0,01
•
efetuar a subtração:
1,42 – 0,01 = 1,41
22,32
•
- achar o logaritmo decimal de 2,00
Log10 2 = 0,301
•
- multiplicá-lo pelo expoente
0,301x2,32 = 0,69832
•
- arredondar o resultado para 3 algarismos significativos.
0,698
Página 8 de 55
Material sujeito a correções
•
encontrar o número que tem este valor por logaritmo decimal.
5,00
π
•
- arredondando para 3 algarismos significativos, vem:
3,14
π + 22,32
•
somando diretamente, vem:
5,00 + 3,14 = 8,14
Cálculo final
1 ,41
= 0 ,173
8 ,14
1.7
Erro de Truncamento
São erros provenientes da utilização de processo que deveriam ser infinitos ou muito
grandes para a determinação de um valor, e que, por razões práticas, são truncados.
Em outras palavras, erro de truncamento de um processo infinito é o erro absoluto do
resultado obtido com um número finito de operações.
1.8
Seqüências – Convergências
Uma seqüência de números reais nada mais é do que um conjunto finito ou infinito de
valores ordenados, x1, x2, x3,..., xn, representado por {xn}, onde xn é chamado termo
geral.
Dizemos que a seqüência é infinita se contiver um número infinito de elementos. Neste
caso podemos dizer que ela converge ou não para um limite, de acordo com a definição.
Definição:
Uma seqüência infinita de números {xn} converge para um valor x, se:
Lim xn − x = 0
n→ ∞
E nesse caso x é o limite da seqüência.
Quando a seqüência é truncada em xn, o erro de truncamento é dado por:
en = xn − x
Página 9 de 55
Material sujeito a correções
Ex.:
A seqüência {xn} com
xn =
1
n converge para o limite “0” porque:
Lim =
n→ ∞
1
−0 =0
n
Exemplo:
Dado x = 0,15, calcular o valor de ex.
Empregando um processo numérico que consiste em substituir a função ex por um
polinômio.
Usando a seqüência:
x2 x3
e ≈1+ x +
....
+
2! 3!
x
Limitando até 4 termos, temos:
e 0 ,15 ≈ 1 + 0 ,15 +
(0 ,15)2 + (0 ,15)3
2
6
= 1,1618125
e 0 ,15 = 1 ,161834243 ± 0 ,5 x10 −4
, isto é, os algarismos até a 8ª casa
Sabendo-se que
decimal são exatos, e comparando este valor com o calculado pelo processo numérico,
verificamos que apenas 5 algarismos significativos são exatos.
Neste caso temos o erro
1,1618342435 − 1,1618125000 = 0,0000217435
Escrevemos então:
Erro de truncamento =
e
0 ,15
2
3

(
0 ,15 ) (0 ,15) 

−  1 + 0 ,15 +
+
 ≤ 0 ,0000217435
2
!
3
!


Que representamos por:
e 0 ,15 = 1,16181 ± 0 ,00003
1.9
Propagação de erros
Exemplos de como os erros vistos podem influenciar o desenvolvimento de um cálculo.
Supondo-se que as operações abaixo sejam processadas em uma máquina com 4 dígitos
significativos e fazendo-se:
x1 = 0,3491x104
e
x2 = 0,002345x100
Página 10 de 55
Material sujeito a correções
Temos:
(x2 + x1) – x1 = (0,002345x100 + 0,3491x104) – 0,3491x104 = 0,3491x104 – 0,3491x104
(4 dígitos) = 0,000
x2 + (x1 – x1) = 0,002345x100 + (0,3491x104 – 0,3491x104) = 0,002345 + 0,000 =
0,002345
Os dois resultados são diferentes quando não deveriam ser. A causa foi o arredondamento
feito na adição (x1 + x2) cujo resultado tem 8 dígitos e a máquina apenas 4.
Página 11 de 55
Material sujeito a correções
2 MATRIZES
Definimos como matriz de ordem mxn, ao conjunto de números aij (i = 1, 2,...,m), (j = 1,
2, ...,n) dispostos em m linhas e n colunas.
Ex.:
...
 a11 a12
a
...
 21 a22
 ...... ....... ......

am 1 am 2 .....
a1n 
a2 n 
......

amn 
Os elementos aij podem ser números, funções ou mesmo matrizes.
Quando m = n temos uma matriz quadrada.
Quando n = 1 temos uma matriz coluna:
 a11 
 a1 
a 
a 
 21  ou  2 
 .... 
 ... 


 
a m 1 
a m 
Quando m = 1, temos uma matriz linha:
[a11 , a12 , a13 ...a1n ]
[a1 , a2 , a3 ,..., an ]
Definições
•
Uma matriz é um conjunto de números, função ou matrizes.
•
Um determinante é uma representação simbólica de um polinômio perfeitamente
definido.
•
Matriz Diagonal é aquela em que aij ≠ 0, para i = j.
a11
0

 0
0
a 22
0



a 33 
0
0
Página 12 de 55
Material sujeito a correções
•
Matriz Unitária é uma matriz quadrada, na qual todos os elementos são nulos exceto
os da diagonal principal que são todos iguais a 1. A matriz unitária de ordem n é
representada por In.
0 .... 0 
1
0
1 .... 0 


In =  ..... .... .... .....


0 ..... 1 
0
•
Matriz Triangular é a matriz na qual aiJ = 0 para i < j (triangular inferior) ou aiJ = 0
para i > j (triangular superior).
Ex.:
•
 a11 0
a
a 22
 12
 .... ....

 a n1 a n 2
....
0 
.... 0 
 (triangular inferior )
.... .... 

.... a nn 
a11 a12
0 a
22

 ..... ....

0
0
.... a1n 
.... a 2 n 
 (triangular superior )
.... .... 

0 a nn 
Matriz Simétrica é toda matriz quadrada onde aiJ = aJi. Os elementos são iguais
simetricamente à diagonal principal.
A = AT
•
Matriz Anti-simétrica é toda matriz em que se tem aij = -aji.
A = -AT
•
Matriz Transposta de uma matriz A de ordem mxn é a matriz At de ordem nxm,
obtida permutando-se as linhas pelas colunas.
•
Matriz Zero é aquela em que todos os seus elementos são nulos.
Página 13 de 55
Material sujeito a correções
Igualdade de Matrizes
Duas matrizes A = (aij) e B = (bij) de ordem mxm, são iguais se e somente se aij = bij.
Adição
Tendo-se as matrizes A = (aij) e B = (bij) de ordem mxn, a adição de A com B será:
C = A + B = (aij + bij) = (cij)
Ex.:
5 4 7 8  3 7 8 5  8 11 15 13
 3 2 1 6 +  0 0 1 2  =  3 2 2 8 

 
 

Subtração
C = A – B = (aij - bij) = (cij)
Ex.:
5 4 7 8  3 7 7 5   2 − 3 0 3 
 3 2 1 6 − 0 0 1 2 =  3
2 0 4 

 
 
Produto de uma Matriz por um número
Se A = (aij) é uma matriz mxn e c um número, temos:
 c .a11
 ....
c.A = A.c = B = 
c .a m 1
... c .a1n 
....
.... 
.... c .a mn 
As seguintes leis são válidas:
A + ( B + C ) = ( A + B ) + C associatividade
( a + b ).A = aA + bA

c( A + B ) = cA + cB 
distributividade
A+ B = B + A
comutatividade
Página 14 de 55
Material sujeito a correções
2.1
Propriedades dos Determinantes
1- Um determinante não se altera quando se trocam as linhas pelas colunas e vice-versa.
2- Trocando-se as posições de duas linhas ou colunas, o determinante fica multiplicado por
(-1).
3- Transpondo-se uma linha ou uma coluna para a primeira posição, o determinante fica
multiplicado por (-1)k-1 onde k representa a ordem da linha ou coluna transposta.
4- Transpondo-se um elemento para a primeira posição, o determinante fica multiplicado
por (-1)k+m onde k representa a ordem da coluna e m a ordem da linha que se cruzam
no elemento transposto.
5- O determinante é nulo se todos os elementos de uma linha ou uma coluna são nulos.
6- O determinante é nulo se os elementos de duas linhas ou colunas são iguais entre si.
7- Se os elementos de uma linha ou coluna são multiplicados por um número, o
determinante fica, também, multiplicado por este número.
8- O determinante não se altera se somarmos aos elementos de uma linha ou coluna os
respectivos elementos de outra linha ou coluna multiplicados por um número.
Consideremos um determinante ∆ e suponhamos que o elemento a transpor seja amk.
Passando a m-ésima linha para a primeira posição e designando ∆’ o novo determinante,
temos:
∆' = (− 1)
m −1
.∆
Passando a k-ésima coluna para a primeira posição, no determinante ∆’ e designando por
∆’’ o novo determinante, temos:
∆'' = (− 1)
k −1
.∆
∆'
Substituindo o valor de ∆’ vem:
∆'' = ( −1 )k −1 .( −1 )m −1 .∆ = ( −1 )k + m − 2 .∆ , e como (-1)-2 = 1, vem :
k +m
∆'' = (− 1)
.∆
Toda matriz que tem duas linhas ou colunas iguais tem determinante nulo.
Trocando-se a posição destas linhas ou colunas o seu valor deveria trocar de sinal.
Página 15 de 55
Material sujeito a correções
Logo:
∆ = -∆
∆
2∆
∆=0
∆=0
2.2
Menor Complementar
Chama-se de menor complementar do elemento aij (Mij), ao determinante de ordem n – 1
extraído de [A], pela supressão da linha e da coluna em que está situado o elemento aij.
 a11 a12
A = a21 a22
a31 a32
a13 
a23 

a33 
Ex.:
O menor complementar de a32 é:
M 32 =
2.3
a11
a13
a21
a23
Complemento Algébrico de um elemento (COFATOR)
Dado o determinante
...
 a11 a12
a
...
 21 a22
 ...... ....... ......

 an1 an 2 .....
Chama-se complemento algébrico ao elemento a i
determinante obtida pela expressão:
j
a1n 
a2 n 
......

ann 
e representa-se por
Aj i
ao
Aij = (− 1) + M ij
i+ j
Consideremos a matriz quadrada:
...
 a11 a12
a
a22
...
 21
[A] =  ...... ....... ......

 an1 an 2 .....
a1n 
a2 n 

......

ann 
Página 16 de 55
Material sujeito a correções
2.4
Matriz Adjunta
[A ]
'
, a matriz cujo elemento
Definimos como matriz adjunta de [A] e representamos por
aij = A ji
A ji
genérico é
onde
representa o complemento algébrico do elemento aij do
determinante associado da matriz [A].
Nestas condições, a matriz adjunta de [A] será:
...
 A11 A21
A
A
...
[A' ] =  12 22
 ...... ....... ......

 A1n A2 n .....
An1 
An 2 

......

Ann 
Como podemos observar, a matriz adjunta pode ser obtida, em outras palavras, a partir da
matriz transposta ([At]), construindo-se uma nova matriz, onde os elementos são os
correspondentes complementos algébricos dos elementos do determinante |At|.
Ex.:
Achar a matriz adjunta de:
[A] = 
a11 a12 

a21 a22 
[A ] = aa
11
t

12
a21 
a22 
Logo a adjunta de A será:
[A' ] = 
a22
 − a21
2.5
− a12 
a11 
Matriz Inversa
Teorema: Para qualquer matriz quadrada A, temos:
[A] [A−1 ] = [A−1 ][ A] = [I ]
Equação (1)
Onde (I) é a matriz unitária.
Definimos como matriz inversa [A] e representamos por [A-1], a matriz tal que seja
satisfeita a expressão (1) .
Página 17 de 55
Material sujeito a correções
Para obtermos [A-1], comecemos por calcular [A].[A’]. Considerando os teorema de Laplace
e Cauchy, resulta:
...
 a11 a12
a
a22
...
 21
 ...... ....... ......

 an1 an 2 .....
a1n   A11 A21
...
a2 n   A12 A22
...
 
...... x  ...... ....... ......
 
ann   A1n A2 n .....
An1   A
0
...
0 


A2 n   0
A
...
0


=

......
...... ....... ...... ......

 
Ann   0
0
..... A 
Pelo que obtivemos, vamos em seguida efetuar o produto:
[A].[ A' ] =
Supondo que
AI
A ≠ φ , temos:
 a11
a
 21
 ....

ann
a12
a22
an 2
 A11

a1n   A
a2 n   A12
x A
 
 ....
ann   A1n

 A
A21
A
A22
A
....
A2 n
A
An1 
A  1

An 2   0
....
A =
 ....
.... ....  
Ann   0

....
A 
....
0
1 .... 0 

... ... ....

0 .... 1 
0
....
Desta ultima igualdade concluímos que:
 A11
 A

 A12
[A-1] =  A
 ....
A
 1n
 A
A21
A
A22
A
....
A2 n
A
An1 
A 

An 2 
....
A  ou
.... .... 
Ann 

....
A 
....
[A ]. [AA' ]
−1
Ex.:
Achar a matriz inversa de:
[A] = 
a11 a12 

a21 a22 
Cálculo de
A
A = a11 .a22 − a12 .a21
Página 18 de 55
Material sujeito a correções
Cálculo de [At]
[A ] = aa
11
t

12
a21 
a22  (poderia ser a transposta da adjunta)
Cálculo de [A’]
[A' ] = 
a22
 − a21
− a12 
a11 
Obtenção de [A-1]
 a
1
. 22
11a22 − a 21a12  − a 21
[A ] = a
−1
− a12 
a11 
A matriz inversa desempenha importante papel na resolução de sistemas de equações
lineares.
Seja o sistema:
a11 .x1 + a12 x2 + ..... + a1n xn = b1

a21 x1 + a22 x2 + ..... + a2 n xn = b2

 ..... ........ ...... ...... ...... ......
an1 x1 + an 2 x2 + ...... + ann xn = bn
Sob forma de produto matricial:
[A][ X ] = [b]
[A ][A][X ] = [A ][b]
−1
−1
Donde:
[X ] = [A−1 ][b]
Página 19 de 55
Material sujeito a correções
Ex.:
Resolver o sistema:
x+ y+z=6
2x − y + z = 3
x + 2y − z = 2
Sob forma matricial temos:
1 1 1   x   6
 2 - 1 1   y  =  3

   
1 2 - 1  z   2
Resultando:
1
 x  1 1
 y  = 2 - 1 1
  

 z  1 2 - 1
−1
 6
 3
 
 2
Cálculo do Determinante (|A|) de A:
1 1 1 1 1
2 - 1 1 2 - 1 = 1 + 1 + 4 − ( −1 ) − 2 − ( −2 ) = 7 , log o A = 7
1 2 -1 1 2
Cálculo da transposta:
1 2 1 
At = 1 - 1 2 

1 1 - 1
[ ]
Cálculo da adjunta:
2
− 1 3
[A' ] =  3 - 2 1 
 5 - 1 - 3 
Página 20 de 55
Material sujeito a correções
Cálculo da Inversa:
[A ]
−1
2
− 1 3
1
1 
=  3 -2
7
 5 - 1 - 3
Donde a solução do sistema será:
 x
 − 1 3 2  6
1
 y  =  3 - 2 1  .  3
  7
  
 z 
 5 - 1 - 3  2
Ou seja:
 x  1
 y  =  2
   
 z   3
Página 21 de 55
Material sujeito a correções
2.6
Cálculo do Determinante
A solução pelo teorema de Laplace torna-se inconveniente no cálculo do determinante de
ordem superior a quarta devido ao grande número de operações envolvidas no processo.
Para contornarmos esta dificuldade usamos um processo que utiliza a 8ª propriedade
anteriormente citada, que permite a redução sucessiva da matriz a uma matriz triangular,
através de operações elementares.
Seja:
 a11 a12
A = a21 a22
a31 a32
a13 
a23 
a33 
a
a 21 a 31
,
,....., n1 ,
a11 a11
a11
Multiplicando-se os elementos da 1ª linha por
e subtraindo estes resultados
dos elementos das linhas 2, 3, 4, ......., n, resulta:
a11
0

A= 0

 ...
 0
a12
a
(1 )
a
(1 )
a
(1)
22
32
...
n2
... ... a1n 
... ... a ( 1 ) 2 n 

(1)
... ... a 3 n 

... ...
... 
... ... a ( 1 ) nn 
Onde:
Primeira coluna abaixo do elemento pivô,
a
a
(1)
a21
= a21 − a11 21 ,.........., an( 11 ) = an1 − a11 n1
a11
a11
Demais elementos das linhas,
(1)
a22
= a22 − a12
a21
a
,.........., a2( 1n ) = a2 n − a1n 21
a11
a11
(1)
a32
= a32 − a12
a31
a
,.........., a3( 1n ) = a3 n − a1n 21
a11
a11
.......................................................................
Página 22 de 55
Material sujeito a correções
Exemplo: Calcular o determinante da matriz a seguir:
1 2 4
A =  5 2 6

 2 1 3
Multiplicando a 1ª linha por
a 21
a11
e subtraindo os resultados das multiplicações de todos os
elementos dos elementos respectivos da 2ª linha vem:
2
4
1
 5 10 20
a21 5



(1 )
= = 5 ⇒  5 2 6  , .então l 2 − l1 ⇒  0 − 8 − 14 etc...
a11 1
 2 1 3 
 2
1
3 
Multiplicando a 1ª linha por
a31
e subtraindo os resultados dos respectivos elementos da 3ª
a11
linha vem:
2
4  1 2
4 
 1
 0


−8
− 14 = 0 − 8 − 14

 

( 2 − 2 ) ( 1 − 4 ) ( 3 − 8 ) 0 − 3 − 5 
Multiplicando a 2ª linha por
4 
1 2
a32 − 3 3 
= ⇒ 0 − 3 − 5 ,25
=
a22 − 8 8
0 − 3
− 5 
Subtraindo-se esta segunda linha obtida da terceira linha, teremos:
2
4
4 
1
 1 2
0
 = 0 − 8 − 14 
−8
−4
 


0 (( −3 ) − ( −3 )) (( −5 ) − ( 5 ,25 )) 0 0 0 ,25
Logo:
∆ = 1 x( −8 ) x 0 ,25 = −2
Página 23 de 55
Material sujeito a correções
3 VALORES E VETORES CARACTERÍSTICOS
Equações homogêneas do tipo:
a11 x1 + a12 x2 + ........... + a1n xn = λx1

a21 x1 + a22 x2 + ........... + a2 n xn = λ x2
AX = 0 = 
 ............................................................
an1 x1 + an 2 x2 + ........... + ann xn = λ xn
São frequentemente encontradas em certos tipos de problemas físicos, onde
parâmetro indeterminado.
λ é um
Representando matricialmente teremos:
AX = λ [ X ]
que tem solução não trivial se o determinante
( a11 − λ )
∆ − λI =
a21
a12 .................a1n
( a12 − λ )................ a 2n
...................................................
an1
an2
( ann − λ )
que conduz à equação polinomial de grau n em
=0
λ:
λn + C1λn −1 + C 2λn − 2 + .......... ... + C n = 0
que é conhecida como equação característica da matriz.
λ
Os valores de
que satisfazem a equação característica da matriz (raízes da equação) A
são os valores característicos de A.
λ
Dos valores de , obtemos os valores dos vetores
denominados Vetores Característicos de A.
X
, (conjuntos de soluções), que são
Exemplo: Determinar os valores e vetores próprios do sistema:
2x2 +
x 3 = λ x1
2 x1 + 10x 2 +
x 3 = λx2
10 x1 +
2 x1 +
x 2 + 10x 3 = λ x3
Página 24 de 55
Material sujeito a correções
Teremos:
( 10 − λ )
∆=
2
2
2
( 10 − λ )
1
1
3
1 = (10 − λ ) − 7(10 − λ ) + 6 = 0
( 10 − λ )
∴
− 3

10 − λ =  1 ⇒
 2

Para
λ1 = 13
Fazendo
Para
Para
 x1 + 2x 2 + x 3 = 0

 2x1 + x 2 + x 3 = 0
 2x + x + x = 0
2
3
 1
1
1
x3 = 1 teremos x1( 2 ) = − , x 2( 2 ) = − e x3( 2 ) = 1
3
3
λ3 = 8
Fazendo
 - 3x1 + 2x2 + x3 = 0

 2x1 - 3x2 + x3 = 0
 2x + x - 3x = 0

1
2
3
x3 = 1 teremos x1(1) = 1, x2(1) = 1 e x3(1) = 1
λ2 = 9
Fazendo
λ1 = 13

λ 2 = 9
λ = 8
 3
 2x1 + 2 x 2 + x3 = 0

 2x1 + 2 x 2 + x3 = 0
 2x + x + 2x = 0
 1
2
3
3
x3 = 1
x ( 3 ) = − , x 2( 3 ) = 1 e x 3( 3 ) = 1
teremos 1
2
Página 25 de 55
Material sujeito a correções
4 SISTEMAS DE EQUAÇÕES LINEARES
O estudo é limitado aos sistemas não homogêneos de “n” equações a “n” incógnitas.
4.1
Métodos Diretos ou de Eliminação
São métodos que determinam a solução de um sistema de equações lineares com um
número finito de operações. Eles atuam diretamente sobre as equações.
4.1.1 Método de Gauss
Consiste em transformar a matriz dos coeficientes das incógnitas em uma matriz triangular
superior, a partir de uma matriz estendida (adicionando-se o vetor independente como
última coluna), através de operações elementares.
(1)
(1)
x1 + a12
x2 + a13
x3 + ........................... + a1(1( n) − 1) xn − 1 + a1(1n) xn = b1(1)
( 2)
x2 + a23
x3 + ........................... + a2( 2( n) − 1) xn − 1 + a2( 2n) xn = b2( 2 )
........................................................................................................
xn − 1 + a((nn−−11))n xn = bn( n−−11)
xn = bn( n )
onde os índices superiores dos coeficientes correspondem ao número de modificações
efetuadas em cada elemento.
Neste caso, a solução do sistema é imediata, mediante a substituição regressiva.
Formando a matriz estendida, justapondo-se o vetor independente, teremos:
a11 a12 ..............a1n b1 


a 21 a 22 ..............a 2 n b2 

Aε =
 ......................................... 


a n1 a n 2 ..............a nn bn 
Começamos as transformações anulando os elementos da coluna 1 abaixo do elemento
a11
, ao qual chamaremos de elemento Pivô.
Gauss prevê dois passos:
1. Dividir
l1
pelo elemento pivô, o que nos dará uma nova linha
2. Para anular o elemento
a 21 é bastante somar l1 a
De um modo geral para se anular o elemento
vetorial:
l1( 1 )
l1(1)
e
pré-multiplicada por
− a21 .
a i 1 ( i = 2...........n ) , executamos a operação
Página 26 de 55
Material sujeito a correções
l i( 1 ) = l i − a i 1l1( 1 )
com
(i = 2......... n) ,
que zera todos os demais elementos da coluna 1 abaixo do elemento pivô.
Desenvolvida para os elementos de todas as linhas equivale a:
 j = 1 ,.........,n + 1
a ij( 1 ) = a ij − a ij a2( 1j ) para 
 i = 2 ,.........., n ,
Ao fim da 1ª eliminação, a matriz
Aε
está transformada em:
(1)
1 a12
..............a1(1n) b1(1) 


(1)
0 a22
..............a2(1n) b (1)
2 
Aε = 

......................................... 
0 a (1) ..............a (1) b (1) 
nn
n 
n2

A segunda eliminação consiste em anular os elementos da segunda coluna, abaixo de
denominado pivô desta eliminação.
(1)
a 22
,
(1)
(2)
l
l
2
2
1. Dividimos
pelo pivô, obtendo
;
(1)
(2)
(1)
(1)
a
l
l
a
32
3
2
32
somamos
a
pré-multiplicada por
2. Para anular o elemento
De um modo geral para se anular o elemento
operação vetorial:
l i( 2 ) = l i(1) − a i(21) l 2( 3 )
com
a i(21 ) ( i = 3...........n ) , executamos a
(i = 3.........n)
,
que se desenvolvida para os elementos de todas as linhas equivale a:
 j = 2 ,.........,n + 1
a ij( 2 ) = a ij( 1 ) − ai(21 )a 2( 1j ) para 
 i = 3 ,.........., n ,
Podemos agora generalizar os procedimentos da 1ª e 2ª eliminação para uma eliminação
genérica “K” que consiste em anular os elementos de
(denominado pivô da k-ésima eliminação.
C k( k − 1 )
abaixo de
( k −1 )
a kk
Página 27 de 55
Material sujeito a correções
Fazemos inicialmente a divisão:
l k( K ) =
que desenvolvida elemento a elemento de
(k )
akj
=
( k −1 )
akj
( k −1 )
akk
l k( k − 1 )
( k −1 ) ,
a kk
l k( k ) , equivale a:
 k = 1 ,............, n
......
 j = k ,............, n + 1 .
Se ‘k’ for menor ‘n’, fazemos as operações vetoriais:
l ik = li( k − 1) − a ik( k − 1) lk( k )
com i = k + 1,........., n
Que desenvolvida elemento a elemento, é:
a
(k )
ij
=a
( k − 1)
ij
−a
( k − 1) ( k )
ik
kj
a
 k = 1 ,.........,n − 1

para  j = k,.........,n + 1
 i = k + 1,.........,n

Exemplo:
2 x1 + 2 x2 + x3 + x4 = 7
x1 - 2 x2 + 2 x3 − x4 = 1
3 x1 + 2 x2 − 3 x3 − 2 x4 = 4
4 x1 + 3 x2 + 2 x3 + x4 = 12
Obtendo a matriz entendida, vem:
l1
l2
l3
l4
1
1
7
2 2
1 − 1 2 − 1 1 


3 2 − 3 − 2 4 


2
1 12
4 3
Página 28 de 55
Material sujeito a correções
1ª Eliminação:
 l1(1)
 (1)
l2
 (1)
l3
 (1)
 l4
= l1 / 2
=
=
l 2 − 1l1(1)
l 3 − 3l1(1)
= l 2 − 4l1(1)






1
0
0
1
−2
−1
0
−1
0,5
0,5
3,5 
1,5 − 1,5 − 2,5 (1.l1(1) ) = 1 1 0,5 0,5 3,5
− 4,5 − 3,5 − 6,5

0
-1
−2 
2ª eliminação:

 ( 2 ) (1 )
l2 = l2 /(−2)
 ( 2 ) (1 )
( 2)
l3 = l3 − (−1)l 2
l ( 2) = l (1) − (−1)l ( 2)
4
4
2






1
1
0
0
0
1
0
0






1
1
0
0
1
0
0
0
3,5 
− 0,75 0,75
1,25 
− 3,25 − 2,75 − 5,25 (−1)(l2( 2) ) = 0 − 1 0,75 − 0,75 − 1,25

− 0,75 − 0,25 − 0,75
0,5
0,5
3ª eliminação:



 (3) (2)
l3 = l3 /(−3,25)
l (3) = l (2) − (−0,75)l (3)
4
3
4





l (4) = l ( 3) /(−0,1907)
4
4






0,5
3,5 
1,25 
1 

0  (−0,75)(l3(3) ) = 0 0 − 0,75 0,3586 − 0,75
0,5
− 0,75
0,75
1
− 0,5238
0
− 0,1907
1
1
0,5
0,5
0
0
1
0
− 0,75
1
0,75
− 0,5238
0
0
0
1

1,25 
1 

0 
3,5
O sistema então ficará:
x1 + x 2 + 0,5 x 3 +
0,5 x4 = 3,5
x 2 − 0,75 x 3 + 0,75 x4 = 1,25
x 3 − 0,5238 x4 = 1
x4 = 0
Que substituindo regressivamente teremos:
x4 = 0
x3 = (0,5238)0 + 1 = 1
x2 = 1,25 + (0,75)1 − (0,75)0 = 2
x1 = 3,5 − 2 − 0,5 x1 − 0,5 x 0 = 1
É importante observar que nenhum dos elementos que servem de pivô numa eliminação ‘k’
Página 29 de 55
Material sujeito a correções
pode ser igual a zero. Se isto ocorrer devemos trocar de posição as (n-k+1) linhas abaixo
de
lk
(inclusive), de modo que tais elementos não sejam nulos.
É óbvio que isto não altera a solução do sistema, porque apenas trocaremos duas equações
de posição.
Quando este procedimento não for possível porque todos os elementos abaixo do pivô são
nulos, i sistema é singular.
Página 30 de 55
Material sujeito a correções
4.1.2 Método de Gauss-Jordan
Se transformarmos a matriz do sistema em uma matriz identidade, a solução do sistema se
apresentará espontaneamente no novo vetor ‘b’ (dos temos independentes).
x1
b1( n )
...
=
=
...
...
...
xn
=
bn( n )
...
...
...
x2
...
...
b2( n )
O método consiste em modificas as eliminações do método de Gauss, para anular em cada
eliminação ‘k’, elementos abaixo e acima do elemento pivô (elemento da diagonal
principal).
Com um procedimento inteiramente análogo ao que nos levou às expressões anteriores (no
método de Gauss),temos para o método de Gauss-Jordan:
Fazemos inicialmente a divisão:
l k( K )
que desenvolvida elemento a elemento de
a kj( k )
=
akj( k − 1 )
( k −1 )
akk
l k( k − 1 )
= ( k −1 ) ,
a kk
lk(k )
, equivale a:
 k = 1,............, n
......
 j = k ,............, n + 1 .
Se “k” for menor “n”, fazemos as operações vetoriais:
l ik = l i( k − 1 ) − aik( k − 1 )l k( k )
com
 i = 1 ,........., n

com i ≠ k
Que desenvolvida elemento a elemento, é:
a ij( k ) = a ij( k − 1 ) − aik( k − 1 )a kj( k )
 k = i,.........,n − 1
 j = k,.........,n + 1

para 
 i = k + 1,.........,n
 j ≠ k
Página 31 de 55
Material sujeito a correções
Exemplo: Usemos o mesmo exercício anterior:
2 x1 + 2 x 2 + x 3 + x4 = 7
x1 - 2 x2 + 2 x3 − x4 = 1
3 x1 + 2 x 2 − 3 x3 − 2 x4 = 4
4 x1 + 3 x2 + 2 x3 + x4 = 12
Obtendo a matriz entendida, vem:
1
1
7
2 2
1 − 1 2 − 1 1 


3 2 − 3 − 2 4 


2
1 12
4 3
1ª Eliminação:
→  l1
 (1)
l2
 (1)
l3
 (1)
 l4
(1)
= l1 / 2
(1)
1
= l 2 − (1)l
= l 3 − ( 3)l1(1)
= l 2 − (4)l1(1)






1
1
0
0
−2
−1
0
−1
3,5 
1,5 − 1,5 − 2,5
− 4,5 − 3,5 − 6,5

0
-1
−2 
0,5
0, 5
2ª Eliminação:
 l1( 2 )

→  l 2( 2 )
 ( 2)
l3
 ( 2)
 l4
= l1(1) − l 2( 2 )
=l
(1)
2
/( −2)
= l 3(1) − ( −1)l 2( 2 )
= l4(1) − ( −1)l 2( 2 )






1
0
0
0
0
1
0
0
1,25
0,25
2,25 
1,25 
− 0,75 0,75
− 5,25 − 2,75 − 5,25

− 0,75 − 0,25 − 0,75
3ª Eliminação:
 l1( 3 )
 ( 3)
l2

→  l 3( 3 )
 ( 3)
 l4
= l1( 2 ) − (1,25)l 3( 3 )
=l
( 2)
2
− ( −0,75)l
=l
( 2)
3
/( −5,25)
( 3)
3
= l4( 2 ) − ( −0,75)l 3( 3 )






1
0
− 0,9047
1,1428
0
1
0,5238
1
0
0
1,1428
0
1
0
0
0
1
0
0
2






Página 32 de 55
Material sujeito a correções
4ª Eliminação:
 l1( 4 )
 ( 4)
l2
 ( 4)
l3
→ l ( 4)
4
= l1( 3 ) − ( −0,9047)l4( 4 ) 1
= l 2( 3 ) − (1,1428)l 4( 4 )  0

= l 3( 3 ) − (0,5238)l4( 4 )  0

0
= l4( 3 ) / 0,1428
0
1
0
0
0
0
1
0
0
0
0
1
1
2
1

0
Logo:
x1 = 1
x2 = 2
x3 = 1
x4 = 0
Valem as mesmas observações feitas para o método anterior, referentes à troca das linhas
caso o pivô na k-ésima eliminação for zero e se esta troca não for possível o sistema é
singular.
Página 33 de 55
Material sujeito a correções
4.1.3 Condensação Pivotal
Os métodos de eliminação são exatos exceto pelos erros de arredondamento que podem
conduzir a soluções errôneas.
Este efeito pode ser diminuído e mesmo evitado mediante a condensação pivotal.
Para isto, rearrumamos as equações, colocando na linha da posição do pivô a linha abaixo
da linha do pivô com o maior elemento absoluto na coluna do pivô.
A condensação pivotal tem por finalidade:
1. Minimizar o erro de arredondamento;
2. Evitar a divisão por zero e
3. Testar a singularidade do sistema.
Exemplo: Resolver o sistema
x1 +
3 x2 + 40 x3 = 38
36 x1 + 106 x2 + 7 x3 = −63
25 x1 +
5 x2 + 12 x3 = 32
Sabendo-se que a solução é (1;-1 e 1) e resolvendo sem a condensação pivotal vem:
3 40 38 
1
 36 106 7 − 63


 25 5 12 32 
1ª Eliminação:
 l1( 1 ) = l1 / 1
3
40
38 
1
 ( 1 )

(1)
 l 2 = l2 − 36l1 0 − 2 − 1433 − 1431
 (1 )
(1)
 l 3 = l3 − 25l1 0 − 70 − 988 − 918 
2ª Eliminação:

40
38 
1 3
 (2) 1

716 ,5
715 ,5 
 l 2 = l2 /( −2 )
0 1
 (2) 1
( 2 ) 0 0 − 51153988 − 51003

 l 3 = l3 − ( −70 )l 2 
Página 34 de 55
Material sujeito a correções
3ª Eliminação:

40
38 
1 3

0 1 716 ,5 715 ,5 



 (3)
2
0 0

1
0
,
99706
l
=
l
/(
−
51153
3
3
Donde:
 x3 = 0 ,99706

 x2 = 715 ,5 − 716 ,5 x 0 ,99706 = 1,07785
 x = 38 − 40 x 0 ,99706 − 3 x1,07785 = −5 ,11595
 1
Fazendo a condensação pivotal:
 36 106 7 − 63
1
3 40 38 

 25 5 12 32 
1ª eliminação
 l1( 1 ) = l1 / 36
0 ,19444
− 1,75 
1 2 ,94444
 ( 1 )


(1 )
 l 2 = l2 − l1
0 − 0 ,05556 − 39 ,80556 − 39 ,75
 (1 )
(1 )
7 ,139
75 ,75 
 l 3 = l3 − 25l1 0 − 68 ,611
2ª Eliminação:

1 2 ,94444


− 68 ,11
 l2 ⇔ l 3 0

0 − 0 ,05556

0 ,194444
7 ,139
− 39 ,80556
− 1 ,75 
75 ,75 
− 39 ,75 
3ª Eliminação:

− 1,75 
1 2 ,9444 0 ,194444
 2

1
1
− 0 ,10405
− 1,10405 
 l 2 = l 2 /( −68 ,611 )
0
 2
1
2
0
− 39 ,81134 − 39 ,81134
 l 3 = l 3 − ( −0 ,05556 )l2 0
Dividindo
l3
por (-39,81134), vem:

40
38 
1 3
 2 1


 l 2 = l 2 /( −68 ,611 ) 0 1 − 0 ,10405 − 1 ,10405
 2 1

1
1
 l 3 = l 3 /( −39 ,81134 )0 0
Página 35 de 55
Material sujeito a correções
Donde:
 x3 = 1

 x2 = −1 ,10405 + 0 ,10405 = −1
 x = −1,75 + 2 ,94444 − 0 ,19444 = 1
 1
Que é uma solução mais adequada que a anterior.
Página 36 de 55
Material sujeito a correções
4.1.4 Refinamento da Solução
É obvio que mesmo com a condensação pivotal, pode persistir algum erro devido aos
arredondamentos.
Podemos, então, fazer um refinamento da solução.
Seja o vetor abaixo a solução obtida:
x ( 0 ) = ( x1( 0 ) , x2( 0 ) ,..........., x1( n ) , )
e a solução exata seja:
x = x( 0 ) + E ( 0 )
onde a
E ( 0 ) é o vetor correção as solução.
Portanto devemos ter:
a11 ( x1( 0 ) + E10 ) + a12 ( x 2( 0 ) + E 2( 0 ) ) + ................. + a1n ( xn( 0 ) + E n( 0 ) ) = b1
a21 ( x1( 0 ) + E10 ) + a22 ( x2( 0 ) + E 2( 0 ) ) + ................. + a2 n ( xn( 0 ) + E n( 0 ) ) = b2
.................................................................................................
an1 ( x1( 0 ) + E10 ) + a n 2 ( x2( 0 ) + E 2( 0 ) ) + ................. + ann ( xn( 0 ) + E n( 0 ) ) = bn
Equações 1
Se substituirmos o valor de
x ( 0 ) no sistema original, teremos:
a11 x1( 0 ) + a12 x2( 0 ) + ................. + a1n xn( 0 ) = b1( 0 )
a21 x1( 0 ) + a22 x2( 0 ) + ................. + a2 n xn( 0 ) = b2( 0 )
.................................................................
an1 x1( 0 ) + an 2 x2( 0 ) + ................. + ann xn( 0 ) = bn( 0 )
Equações 2
Página 37 de 55
Material sujeito a correções
Subtraindo as equações 2 das equações 1 e definindo
β ( 0 ) = b − b( 0 ) , vem:
a11 E1( 0 ) + a12 E2( 0 ) + ................. + a1n En( 0 ) = β 1( 0 )
a21 E1( 0 ) + a22 E 2( 0 ) + ................. + a2 n E n( 0 ) = β 2( 0 )
..................................................................
an1 E1( 0 ) + an 2 E 2( 0 ) + ................. + ann En( 0 ) ) = β n( 0 )
x
Resolvendo este último sistema, encontramos um vetor , aproximação de
podemos ter:
E( 0 )
, e
x = x( 0 ) + x( 1 )
até que tenhamos valores que satisfaçam o erro requerido.
Exemplo: Fazer o refinamento do problema anterior resolvido sem condensação pivotal e se
tivéssemos encontrado raízes (-5,1195; 1,07785 e 0,99706):
Calculamos o vetor residual
β (0):
b1( 0 ) = 1( −5 ,11595 ) + 3( 1,07785 ) + 40( 0 ,99706 ) = 38
b2( 0 ) = 36( −5 ,11595 ) + 106( 1 ,07785 ) + 7( 0 ,99706 ) = −62 ,94268
b3( 0 ) = 25( −5 ,11595 ) + 5( 1,07785 ) + 12( 0 ,99706 ) = −110 ,54478
Então:
β 1( 0 ) = b1 − b1( 0 ) = 38 − 38 = 0
β 2( 0 ) = b2 − b2( 0 ) = −63 − ( −62 ,94268 ) = −0 ,05732
β 3( 0 ) = b3 − b3( 0 ) = 32 − ( −110 ,54478 ) = 142 ,54478
(0)
E
O vetor
será obtido pela resolução do sistema:
E1( 0 ) + 3 E 2( 0 ) + 40 E 3( 0 ) = 0
36 E1( 0 ) + 106 E 2( 0 ) + 7 E 3( 0 ) = −0 ,05732
25 E1( 0 ) + 5 E 2( 0 ) + 12 E 3( 0 ) = 142 ,54478
Trocando-se as 1ª pela 2ª linhas (condensação pivotal), vem:
 36 106 7 − 0 ,05732 
1

3 40
0


 25 5 12 142 ,54478
Página 38 de 55
Material sujeito a correções
l11 = l1 / 36  1
1

 25
2 ,94444 70 ,19444
3
40
5
12
− 0 ,00159 

0

142 ,54478
1ª eliminação:
70 ,19444
− 0 ,00159 
1 2 ,94444
0 − 0 ,05556 − 39 ,80556 − 0 ,00159 


0
68 ,111
− 7 ,139
− 142 ,58453
Fazendo a condensação pivotal, vem:
70 ,19444
− 0 ,00159 
1 2 ,94444
0
68 ,111
− 7 ,139
− 142 ,58453

0 − 0 ,05556 − 39 ,80556 − 0 ,00159 
2ª eliminação:
1 2 ,94444 70 ,19444 − 0 ,00159
0
1
− 0 ,10481 − 2 ,09341

0
0
− 39 ,79974 − 0 ,11785 
1 2 ,94444 70 ,19444 − 0 ,00159
0
1
− 010981 − 2 ,09341

l 3( 4 ) = l 3( 3 ) / 39 ,79974 0
0
1
0 ,00296 
 x3( 1 ) = 0 ,00296

(1 )
 x2 = −2 ,09341 + 0 ,10981( 0 ,00296 ) = −2 ,09308
 (1 )
 x1 = −0 ,00159 − ( 70 ,19444( 0 ,00296 )) − 2 ,94444( −2 ,09308 ) = 5 ,95359
Logo a solução aproximada é:
 x1 = −5 ,11595 + 5 ,95359 = 0 ,83764

 x 2 = 1 ,07785 − 2 ,09308 = −1 ,01523
 x = 0 ,99706 + 0 ,00296 = 1 ,00002
 3
Página 39 de 55
Material sujeito a correções
4.1.5 Inversão de Matrizes
Um algoritmo de execução extremamente simples para inverter uma matriz
ser obtido por uma adaptação do método de Gauss-Jordan.
A(mxn)
pode
Seja a matriz 3x3:
 a11 a12
A = a21 a22

a31 a32
Onde
A ≠0
a13 
a23 

a33 
e a sua inversa (B) é:
 b11 b12
B = b21 b22
b31 b32
b13 
b23 
b33 
Chamemos os 3 vetores coluna da matriz inversa de
teremos:
 a11 a12
A = a21 a22
a31 a32
a13   b11 b12
a23  x b21 b22
a33  b31 b32
b1 , b2 e b3 . Por definição de inversa
b13  1 0 0
b23  = 0 1 0
b33  0 0 1
Quando consideramos a formação da primeira coluna da matriz identidade pela
multiplicação de
A x b1 , podemos dizer que:
 a11 a12
A = a21 a22
a31 a32
Logo, para determinar a primeira coluna
a13   b11  1
a23  x b21  = 0
a33  b31  0
b1 , da matriz inversa, basta resolver o sistema:
A x b1 = e1 , onde e1 = (1 0 0 )
t
O que valeu para a primeira coluna vale para as outras duas. Assim para obter
resolvemos os sistemas:
b2
e
b3
,
A x b2 = e2 , onde e2 = (0 1 0)t
A x b3 = e3 , onde e3 = (0 0 1)t
Os três sistemas podem ser resolvidos pelo método de Gauss-Jordan.
Como eles têm a mesma matriz (A), poderemos resolvê-los simultaneamente, pois as
eliminações feitas em A, seriam exatamente as mesmas se as resoluções fossem feitas
Página 40 de 55
Material sujeito a correções
separadamente. As únicas modificações estarão nos termos independentes das incógnitas,
o que contornamos trabalhando com uma matriz estendida (3x6).
 a11 a12
∆E = a21 a22
a31 a32
a13
a23
a33
1 0 0
0 1 0
0 0 1
Fazemos então as eliminações de Gauss-Jordan na matriz
solução
b1
aparecerá na 4ª coluna,
b2
na 5ª e
b3
∆E
, ao fim das quais o vetor
na 6ª.
Exemplo: Seja a matriz a inverter (já acrescida da matriz identidade):
l1  1 3 1 1 0 0
l 2  2 4 3 0 1 0
l 3  − 1 1 0 0 0 1
1ª Eliminação:
l1( 1 ) = l1 / 1
1 3 1 1 0 0
l 2( 1 ) = l 2 − 2l1( 1 ) 0 − 2 1 − 2 1 0

l 3( 1 ) = l 3 − ( −1 )l1( 1 ) 0 4 1 1 0 1
2ª Eliminação:
l1( 2 ) = l1( 1 ) − 3l 2( 2 ) 1 0 2 ,5 − 2 1 ,5 0
l 2( 2 ) = l 2( 1 ) /( −2 ) 0 1 − 0 ,5 1 − 0 ,5 0


l 3( 2 ) = l 3( 1 ) − 4l 2( 2 ) 0 0
3
−3
2
1
3ª Eliminação:
l1( 3 ) = l1( 2 ) − 2 ,5l 3( 3 )
l 2( 3 ) = l 2( 2 ) − ( −0 ,5 )l 3( 3 )
l 3( 3 ) = l 3( 2 ) / 3
1 0 0 0 ,5 − 0 ,16666 − 0 ,83333
0 1 0 1 − 0 ,16666 0 ,16666 


0 0 1 − 1 0.66666
0 ,33333 
Logo a matriz inversa é:
0 ,5 − 0 ,16666 − 0 ,83333
 1 − 0 ,16666 0 ,16666 

 . È óbvia a generalização do processo.
 − 1 0 ,66666
0 ,33333 
Página 41 de 55
Material sujeito a correções
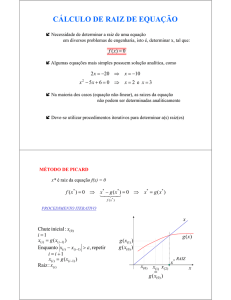
5 SISTEMAS DE EQUAÇÕES LINEARES
O estudo é limitado aos sistemas não homogêneos de “n” equações a “n” incógnitas.
5.1
Métodos Iterativos
Métodos Iterativos consistem em se escrever o sistema
AX = b
sob a forma:
x = F ( x) + d
Onde
F
é uma matriz (m x n) e d é um vetor (
d ∈ Rn
Deste modo, partindo de uma aproximação inicial
1a
x (0)
).
, fazemos as iterações:
x (1) = F ( x ( 0 ) + d
2 a x ( 2 ) = F ( x (1) + d
...................................
e de um modo geral, se fizermos, ‘K’ iterações, obteremos a solução aproximada na
iteração ‘k+1’, pela fórmula de recorrência:
x ( k + 1) = F ( x ( k ) ) + d
Se:
x
Lim
k →∞
(k )
−x =0
→∞
diremos que a seqüência de aproximações
que a seqüência diverge.
x (k )
converge para
x
. Caso contrário, diremos
Página 42 de 55
Material sujeito a correções
5.2 Método de Jacobi
O método de Jacobi consiste na escolha da seguinte matriz
F
:
x1(1) =
1
(b1 − a12 x 2( 0 ) − a13 x 3( 0 ) − ............... − a1n x n( 0 ) )
a11
x 2(1) =
1
(b2 − a 21 x1( 0 ) − a 23 x 3( 0 ) − ............... − a 2 n x n( 0 ) )
a 22
......................................................................
x n(1) =
1
(bn − a n1 x1( 0 ) − a n 2 x 2( 0 ) − ............... − a1( n − 1) x n( 0−)1 )
a nn
Exemplo: Seja o sistema:
 2 x1 − x2 = 1,

 x1 + 2 x2 = 3
cuja solução é x1 = 1 e x 2 = 1
Solução:
Transformando de acordo com a disposição anterior, teremos:
1
x1 = (1 + x2 )
2
1
x2 = ( 3 − x1 )
2
Fazendo
x1 = x 2 = 0 , teremos:
1ª Iteração:
1
x1(1) = (1 + 0) = 0,5
2
1
x2(1) = ( 3 − 0) = 1,5
2
2ª Iteração:
1
x1( 2 ) = (1 + 1,5) = 1,25
2
1
x2( 2 ) = ( 3 − 0,5) = 1,25
2
Página 43 de 55
Material sujeito a correções
3ª Iteração:
1
x1( 3 ) = (1 + 1,25) = 1,125
2
1
x2( 3 ) = ( 3 − 1,25) = 0,825
2
4ª Iteração:
1
x1( 4 ) = (1 + 0,825) = 0,9125
2
1
x2( 4 ) = ( 3 − 1,125) = 0,9375
2
Página 44 de 55
Material sujeito a correções
5.3 Método de Gauss-Siedel
É análogo ao método de Jacobi, com uma alteração esperada, em função da seguinte
modificação:
Quando na 1ª iteração calculamos
pode, portanto, ser usado.
x 2(1)
, já dispomos do valor de
x1(1)
que
Analogamente, podemos proceder assim para as demais iterações.
Teremos então na 1ª iteração e genericamente até a
k +1
-ésima:
x1( k + 1) =
1
(b1 − a12 x2( k ) − a13 x3( k ) − ............... − a1n xn( k ) )
a11
x2( k + 1) =
1
(b2 − a21 x1( k + 1) − a23 x3( k ) − ............... − a2 n xn( k ) )
a22
............................................................................................
1
xn( k + 1) =
(bn − an1 x1( k + 1) − an 2 x2( k + 1) − ............... − a1( n − 1) xn( k−)1 )
ann
Exemplo:
Seja o mesmo sistema anteriormente visto pelo método de Jacobi:
 2 x1 − x2 = 1

 x1 + 2 x2 = 3
Onde:
1
x1 = (1 + x2 )
2
1
x2 = ( 3 − x1 )
2
1ª Iteração:
1
( 1 + 0 ) = 0 ,5
2
1
= ( 3 − 0 ,5 ) = 1 ,25
2
x1( 1 ) =
x2( 1 )
Página 45 de 55
Material sujeito a correções
2ª Iteração:
1
x1( 2 ) = (1 + 1,25) = 1,125
2
1
x2( 2 ) = ( 3 − 1,125) = 0,973
2
3ª Iteração:
1
x1( 3 ) = (1 + 0,9375) = 0,9690
2
1
x2( 3 ) = ( 3 − 0,9690) = 1,0160
2
4ª Iteração:
1
x1( 4 ) = (1 + 1,0160) = 1,008
2
1
x2( 4 ) = ( 3 − 1,008) = 0,996
2
5.4 Estudo da Convergência
Os métodos iterativos convergem sejam quais forem os valores iniciais adotados, desde
que em cada uma das equações a soma dos valores absolutos dos
n
aij
∑a
j =1
j≠i
aij
seja menor que 1.
< 1 para ( i = 1,2,........n)
ii
ou:
n
∑ aij
< a11 para ( i = 1,2,........n )
j =1
j≠i
Exemplo:
10 x1 +
2 x2 + x3 = 9
2 x1 + 20 x2 − 2 x3 = 44
− 2 x1 + 3 x2 + 10 x3 = 22
Página 46 de 55
Material sujeito a correções
6 Decomposição LU
Inicialmente veremos em que condições podemos decompor uma matriz quadrada A = (aij)
no produto de uma matriz triangular inferior por uma matriz triangular superior.
6.1
Teorema LU
Seja A = (aij) um matriz quadrada de ordem n, e Ak o menor principal, constituído das k
primeiras linhas e k primeiras colunas de A assumimos que det (Ak) ≠ 0 para k = 1, 2,..., n
–1. Então existe uma única matriz triangular superior U = (uij) tal que LU = A. Além disso,
det (A) = u11u12...umn.
Prova
Para provar este teorema usaremos a indução sobre n.
1. Se n = 1, temos que: a11 = 1. a11 = 1.u11 unicamente, e assim A = LU, onde L =
1 e U = u11. Além disso, det (A) = u11.
2. Assumimos que o teorema é verdadeiro para n = k – 1, ou seja, que toda matriz de
ordem k – 1 é decomponível no produto LU nas condições do teorema.
3. Devemos mostrar que a decomposição pode ser feita para uma matriz de ordem n
= k, seja, então, A uma matriz de k. Partimos esta matriz em sub-matrizes da
 Ak −1
A =  st

forma:
r 
a kk  , onde r e s são vetores coluna, ambos com k
– 1 elementos.
Note que a matriz Ak – 1 é de ordem n k – 1 e satisfaz as hipóteses do teorema. Portanto
pela hipótese de indução esta pode ser decomposta na forma
Ak −1 = Lk −1U k −1
Utilizando as matrizes Lk-1 e Uk-1, formamos:
 Lk −1
L =  m t
0
1 ;
U k −1
U=  0

p 
ukk 
Onde m e p são vetores coluna, ambos com k – 1 componentes (mt é a transposta de m).
m, p e ukk são desconhecidos. Assim, impondo que a matriz A seja decomponível em LU
vamos tentar determiná-los.
Página 47 de 55
Material sujeito a correções
Efetuando o produto LU, segue que:
 Lk −1
L =  m t
0
1 *
U k −1
U=  0

p 
 Lk −1U k −1
LU =  t

ukk  ⇒
 m U k −1
Lk −1 p 
m p + ukk 
t
Estudemos agora a equação LU=A, isto é:
 Lk −1U k −1
 m tU
k −1

Lk −1 p   Ak −1
=
m t p + ukk   s t
r 
a kk 
Da igualdade acima concluímos que:
Lk − 1U k − 1
=
Lk − 1 p
r
=
t
m U k −1
=
m t p + ukk
Ak − 1
;
;
st
=
;
a kk
.
Observe que a primeira equação é válida para a hipótese de indução e, portanto Lk-1 e Uk-1
são univocamente determinadas. Além disso, nem Lk-1 e nem Uk-1 são singulares (ou Ak-1
também seria singular, contrariando a hipótese). Assim de:
Lk −1 p
=
m t U k −1
r
=
m t p + ukk
st
=
a kk
⇒
p = L−1 k −1 r ;
⇒
m t = s t U − 1 k −1
⇒
ukk = a kk − m t p
Portanto p, m e ukk são determinados univocamente.
Finalmente,
Det(A) = det(L).det(U)
Det(A) = 1.det(Uk-1).Ukk
Det(A) = u1.u2....uk-1.ukk,
Completando a prova.
Página 48 de 55
Material sujeito a correções
6.2
Esquema prático para a decomposição LU
Observe que teoricamente, para obtermos as matrizes L e U, devemos calcular as
inversões de Lk-1 e Uk-1. Entretanto, na prática podemos calcular L e U simplesmente
aplicando a definição de produto e de igualdade de matrizes, isto é, impondo que LU = A.
Seja então,
1
l
 21
 l 31


 l n1

0
1
l 32
0
0
1
:
l n2
...
...
.
. ..
... l n( n−1)
0  u11
0  0

:  0
 * 
0 
1  0
u12
u22
0
:
...
u13
u23
u33
...
...
...
...
..
0
u13 
α 11

α
u23 
 21
α 31
u33 
 = 
: 
 :
α n1
unn 
α 12 α 13
α 22 α 23
α 32 α 33
:
:
α n2
α n3
...
...
...
:
...
α 1n 
α 2 n 
α 3n 

: 
α nn 
Para obtermos os elementos da matriz L e da matriz U devemos calcular os elementos das
linhas de U e os elementos das colunas de L. Isto pode ser feito efetuando o produto de L
por U.
1. Produto da 1ª linha de L pelas colunas de U igualadas aos elementos da 1ª coluna
de A
1.u11 + 0.0 + ...+ 0.0 = a11
1.u11 = a11
⇒ u11 = a11
1.u12 = a12
⇒ u12 = a12
.....
..... .... .... ....
1. u1n = a1n
⇒ u1n =
a1n
Generalizando,
u1j = a1j, j = 1, 2, ...,n
2. Produto de todas as linhas de L (da 2ª até nª), pela 1ª coluna de U igualada com os
elementos da 1ª coluna de A (abaixo da diagonal principal):
l 21 u11 = a 21 ⇒ l 21 =
a 21
u11
l 31 u11 = a 31 ⇒ l 31 =
a 31
u11
...
...
...
...
l n1 u11 = a n1 ⇒ l n1 =
a n1
u11
Página 49 de 55
Material sujeito a correções
Generalizando,
l i1 =
a i1
, i = 2,..., n
u11
3. Produto da 2ª linha de L por todas as colunas de U (da 2ª até nª), igualadas aos
elementos de 2ª linha de A (da diagonal principal em diante)
l 21 u12 + 1.u22 + 0 * 0 + ... + 0 * 0 = a 22
l 21 u12 + u22 = a 22 ⇒ u22 = a 22 − l 21 u12
l 21 u13 + u23 = a 23 ⇒ u23 = a 23 − l 21 u13
...
...
...
...
l 21 u1n + u2 n = a 2 n ⇒ u2 n = a 2 n − l 21 u1n
Generalizando,
u2 j = a 2 j − l 21 u1 j , j = 3,...n
4.
O produto de todas as linhas de L (da 3ª até a nª) pela 2ª coluna de U igualando
aos elementos da 2ª coluna de A (dada diagonal principal em diante):
l 31U 12 + l 32U 22 = a 32 ⇒ l 32 =
a 32 − l 31U 12
U 22
l 41U 12 + l 42U 22 = a 42 ⇒ l 42 =
a 42 − l 41U 12
U 22
l n1U 12 + l n 2U 22 = a n 2 ⇒ l n 2 =
li2 =
a n 2 − l n1U 12
U 22
a i 2 − l i 2U 12
, i = 3,..., n
U 22
Se continuarmos calculando a 3ª linha de U, 3ª coluna de L, 4ª linha de U, 4ª coluna de L,
etc..., teremos de fórmulas gerais:
Página 50 de 55
Material sujeito a correções
i −1

 uij = a ij − ∑ l ik ukj ,
k =1


i −1

a ij − ∑ l ik ukj

k =1
 l ij =
,
u jj

i≤ j
i> j
Aplicação à solução de problemas
Seja o sistema Ax = b de ordem n, onde A satisfaz as condições da decomposição LU.
Então o sistema Ax = b pode ser escrito como:
Ax = b
Logo:
LUx = b
Fazendo
Ux = y
A solução se reduz a:
Ly = b
Resolvendo o sistema anterior, encontramos y e substituindo y e m Ux = y encontramos x.
Página 51 de 55
Material sujeito a correções
Exemplo de decomposição LU
Dado o sistema:
 2 x + 3y - z = 4

+ 2z = 3
 x

3y - z = 2

Com esse sistema formamos duas matrizes
 2 3 − 1
1 0 2 

A= 
0 3 − 1
e
 4
 3
B=  
 2
Temos a fórmula Ax = B
Então fazemos A= L*U, Sendo:
L = Matriz Triangular inferior (lower) de diagonal unitária
U= Matriz Triangular Superior (upper)
 1 0 0
 l 21 1 0

L= 
 l 31 l 32 1
e
 u11 u12 u13 
 0 u 22 u 23

U= 
 0
0 u 33
Multiplicando as matrizes L e U e igualando à matriz A, conseguimos obter todas as
incógnitas das matrizes L e U:
 1 0 0
 l 21 1 0

L= 
 l 31 l 32 1
*
 u11 u12 u13 
 0 u 22 u 23

U= 
 0
0 u 33
=
 2 3 − 1
1 0 2 


A=
0 3 − 1
Página 52 de 55
Material sujeito a correções
≤
# Primeira linha de L multiplicando a primeira coluna de U: (i j)
(1* u11) + (0 * 0) + (0 * 0) = a11
u11 + 0 +0= 2
u11 =2
≤
#Primeira linha de L multiplicando a segunda coluna de U: (i j)
(1* u12) + (u13 * 0) + (0 * 0) = a12
u12 + 0 +0= 3
u12 =3
≤
#Primeira linha de L multiplicando a terceira coluna de U: (i j)
1* u13) + (u23 * 0) + (u33 * 0) = a13
u13 + 0 +0= -1
u13 = -1
#Segunda linha de L multiplicando a primeira coluna de U: (i > j)
(l21 * u11) + (0 * 0) + (0* 0) = a21
2 l21 = 1
l21 = 1/2
≤
#Segunda linha de L multiplicando a segunda coluna de U: (i j)
(l21 * u12) + (u22 * 1) + (0* 0) = a22
(3 * ½) + u22 = 0
3/2 . u22 = 0
u22 = -3/2
≤
#Segunda linha de L multiplicando a terceira coluna de U: (i j)
(l21 * u13) + (1* u23) + (0 * u33) = a23
(1/2 *(-1)) + (u23 + 0) = 2
(-1/2* u23) + 0 = 2
u23 = 2 + l/2
4+1
u23 = 2
u23 = 5/2
Página 53 de 55
Material sujeito a correções
#Terceira linha de L multiplicando a primeira coluna de U: (i > j)
(l31 * u11) + (l23* 0) + (0 * 0) = a31
(l31* 2) + 0 + 0 = 0
l31 = 0
#Terceira linha de L multiplicando a segunda coluna de U: (i > j)
(l31* u12) + (l32* u22) + 0 * 0 = a32
(0/2 * 3) + l32 - 3/2 + 0 = 3
(-3/2. l32) + 0 = 3
-3.l32 = 3*2
-3l32 = 6
l32= 6/3
l32 = 2
≤
#Terceira linha de L multiplicando a terceira coluna de U: (i j)
(l31* u13) + (l32* u23) + (1 * u33) = a32
(0/2 * 3) + 2 - 5/2 + u33 = -1
0-10/2 u33 = -1
u33 = -1+5
u33 = 4
Matriz Fatorada:
0 0
 1
1 / 2 1 0

L= 
 0 − 2 1
*
3
−1
2
 0 − 3 / 2 5 / 2

U= 
0
0
4 
=
 2 3 − 1
1 0 2 

A= 
0 3 − 1
Voltando à fórmula Ax = B, como A = L* U obtemos LUx = B
Agora substituiremos Ux por Y e obtemos a fórmula LY = B, onde
0 0
 1
Y1 
 
1 / 2 1 0
 * Y = Y2  = B =
L= 
Y3 
 0 − 2 1
 4
 3
 
 2
Fazendo a multiplicação das matrizes (L e Y) e igualando à matriz B obtemos um Sistema
Triangular Inferior de diagonal unitária.
Página 54 de 55
Material sujeito a correções
Resolvendo-o teremos:
Y1 = 4,
Y2 = 1
e
Y3 = 4
Como Ux = Y e os valores de U e Y já são conhecidos utilizaremos o mesmo
método utilizado para achar Y
1,
Y2 , Y3 . Fazendo a multiplicação das matrizes U e X (X1,
X2, X3) e igualando à matriz Y, obtemos um SISTEMA TRIANGULAR SUPERIOR.
Resolvendo-o teremos:
3
−1
2
 0 − 3 / 2 5 / 2

U= 
0
0
4 
 X1 
X 
* X = 2
 X 3 
=
Y1 
Y 
Y = 2
Y3 
Donde:
X1 = 1
X2 = 1
X3 = 1
Tirando a Prova
Conforme a fórmula Ax = B, verificamos se os resultados obtidos X1, X2 e X3 satisfazem as
condições da mesma, para isso multiplicaremos as matrizes A e X e igualamos à matriz B.
Comparando os valores obtidos do produto AX com B, saberemos se encontramos a
solução correta.
 2 3 − 1
1 0 2 

A= 
0 3 − 1
*
 X1 
X 
X =  2
 X 3 
=
 4
 3
B=  
 2
Página 55 de 55