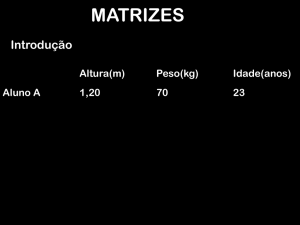
MATRIZES
Introdução
Aluno A
Altura(m)
Peso(kg)
Idade(anos)
1,20
70
23
MATRIZES
Introdução
Altura(m)
Peso(Kg)
Idade(anos)
Aluno A
1,70
70
23
Aluno B
1,75
60
45
Aluno C
1,60
52
25
Aluno D
1,81
72
30
MATRIZES
Introdução
1, 7 0
1, 7 5
1, 6 0
1,
8
1
70
60
52
72
23
45
25
30
MATRIZES
Definição: Dados dois números m e n naturais e não nulos, chama-se matriz
m por n toda tabela M formada por números reais distribuídos em
m linhas e n colunas.
EXEMPLOS:
3
M=
0
A=
[0
5
4
5
−1
2
9 −1 7]
É matriz 2 x 3
É matriz 1 x 4
MATRIZES
a11 a12
a
a22
21
M=
...
...
am1 am2
... a1n
... a2n
... ...
... amn m x n
a11 a12
a
a22
21
A=
...
...
am1 am2
a1n
... a2n
... ...
... amn m x n
...
aij
a11
a22
am1
a2n
amn
i = linha
j = coluna
( )
M = aij
mxn
MATRIZES
Matrizes Especiais
• Matriz Linha
• Matriz Coluna
• Matriz Nula
• Matriz Quadrada
• Matriz Diagonal
• Matriz Identidade
• Matriz Transposta
EXEMPLOS:
M = [0 9 −1 7]
Matriz que possui
1x4
A = [a11 a12 a13 a14 a15 a16 ]
uma única linha
1x6
MATRIZES
Matrizes Especiais
• Matriz Linha
• Matriz Coluna
• Matriz Nula
• Matriz Quadrada
• Matriz Diagonal
• Matriz Identidade
• Matriz Transposta
EXEMPLOS:
0
M= 9
−1
7
A=
4x1
a11
a
21
a31
a41
a51
a61
Matriz que possui
uma única Coluna
6x1
MATRIZES
Matrizes Especiais
• Matriz Linha
• Matriz Coluna
• Matriz Nula
• Matriz Quadrada
• Matriz Diagonal
• Matriz Identidade
• Matriz Transposta
EXEMPLOS:
Matriz que possui
0 0
M = 0 0
0 0
A=
0 0 0
0 0 0
todos os elementos
iguais a zero
2x3
3x2
MATRIZES
Matrizes Especiais
• Matriz Linha
• Matriz Coluna
• Matriz Nula
• Matriz Quadrada
• Matriz Diagonal
• Matriz Identidade
• Matriz Transposta
EXEMPLOS:
Diagonal
Diagonal
secundária
principal
M=
0
7
−3
4
9
1
2
5
−1
2
2
Diagonal
Diagonal
principal
secundária
A=
a11 a12
a
a
21 22
número de linhas igual
2x2
3x3
i=j
i=j
Matriz que possui o
ao número de colunas
MATRIZES
Matrizes Especiais
• Matriz Linha
• Matriz Coluna
• Matriz Nula
• Matriz Quadrada
• Matriz Diagonal
• Matriz Identidade
• Matriz Transposta
EXEMPLO:
M=
0
a11 0
0 a
0
22
0 a33
0
É a matriz quadrada que apresenta
todos os elementos,não pertencentes
a diagonal principal, iguais a zero
3x3
MATRIZES
Matrizes Especiais
• Matriz Linha
• Matriz Coluna
• Matriz Nula
• Matriz Quadrada
• Matriz Diagonal
• Matriz Identidade
• Matriz Transposta
EXEMPLO:
M=
1 0 0
0 1 0
0 0 1
É a matriz diagonal que apresenta
todos os elementos da diagonal
principal iguais a 1
3x3
MATRIZES
Matrizes Especiais
• Matriz Linha
• Matriz Coluna
• Matriz Nula
• Matriz Quadrada
• Matriz Diagonal
• Matriz Identidade
• Matriz Transposta
EXEMPLO:
M=
0 1
1
2 −-1
1
3
23 x 2
3x2
0
Mt =
1
3
1
−1
2
Matriz obtida de A trocando-se,
2
“ordenadamente”, suas linhas
2x3
por colunas.Indicamos a matriz
transposta de A por At.
2x3