LISTA 11 Velocidade Instantânea

Universidade Tecnológica Federal do Paraná - UTFPR
Disciplina de Física Teórica I
Prof. Nelson Elias
11ª Lista de Exercícios: Velocidade instantânea, aceleração instantânea e Mov. com aceleração variável.
Aluno (a): _______________________________________ Turma: _______ Data: ______/_____/________
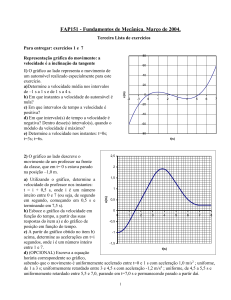
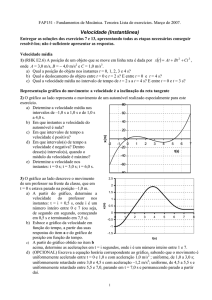
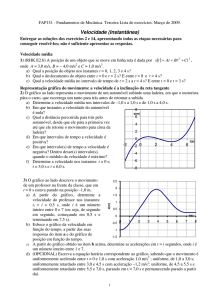
1) A posição de uma partícula em função do tempo está dada pela curva que aparece na figura abaixo.
a) Determine a velocidade instantânea no instante t = 2 s.
b) Observe o gráfico x versus t e responda:
Em que instante essa velocidade é máxima?
Em que instante é nula? Em algum instante é negativa.
Resp. a) v ≈ 1,5 m/s e b) vizinhanças de 4 s, t= 0 s e t = 6 s; um pouco antes do zero e depois do 6 s.
2) A posição de uma certa partícula depende do tempo de acordo com a equação:
posição é medida em metros e t em segundos.
a) Encontre o deslocamento e a velocidade média para o intervalo 3,0 s ≤ t ≤ 4,0 s.
b) Encontre a fórmula geral para o deslocamento no intervalo de tempo de t a t + ∆t.
c) Use o processo de limite para obter a velocidade instantânea em qualquer tempo t.
x(t) = t2 – 5,0t + 1 onde a
3) Uma equação para a posição de uma partícula em movimento é dada por x (t) = b t2 - c t3.
a) Quais as unidades de b e c para que a posição seja dada em unidades SI.
b) Considerando b = 6,0 unidades do SI e c = 1,0 unidades do SI.
Quando, se ocorrer, a velocidade da partícula é zero?
Resp. a) b = m/s2 e c = m/s3; b) t= 0 s e t = 4 s
4) Um movimento é dado pela expressão x(t) = 10 – 2t + ½ t2 onde a posição é medida em metros e t em segundos.
Determine: a) A equação da velocidade instantânea em função do tempo;
b) Verifique se o móvel muda de sentido, se mudar, determine a posição em que isto ocorre;
c) Em que instante o móvel passa pela origem, se isso acontecer;
d) Qual o aspecto do gráfico da posição em função do tempo, e da velocidade em função do tempo.
Resp. a) v (t) = -2 + t ; b) sim, t = 2 s e x = 8 m e c) nunca.
5) (a) A posição de uma partícula é dada por x(t) = 20t - 5t3, com x em metros e t em segundos. Quando, se ocorrer a
velocidade da partícula é zero? (b) Quando a aceleração é zero? (c) Quando a aceleração é negativa? Positiva? (d) Trace
um esboço do gráfico de x(t), v(t), a(t).
Resp. a) t =1,15s ; b) t = 0 s; c) a sempre negativa.
6) A posição de uma partícula que se move ao longo do eixo x é dada em centímetros por x(t) = 9,75 + 1,50 t3, onde t
está em segundos. Calcule (a) a velocidade média durante o intervalo de tempo t = 2,00 s até t = 3,00 s, (b) a velocidade
instantânea em t = 2,00 s; (c) a velocidade instantânea em t = 3,00 s; (d) a velocidade instantânea em t = 2,50 s; e (e) a
velocidade instantânea quando a partícula estiver no meio do caminho entre suas posições em t = 2,00 s e t = 3,00 s. (f)
Trace o gráfico de x contra t e mostre as suas respostas graficamente.
Resp. a) vmed = 28,5 m/s i; b) v(2s) = 18 cm/s; c) v (3s) = 40,5 cm/s; d) v (2,5s) = 28,125 cm/s; e) v(2,597) = 30,45 cm/s.
7) A posição de um objeto em movimento retilíneo é dada por x(t) = 3t - 4t2 + t3, onde x está em metros e t em
segundos. Determine:
a) Qual a posição do objeto no instante 4 s ?
b) Qual o vetor posição do objeto no instante 4 s?
c) Qual a velocidade média (vetor) no intervalo t = 2 s a t = 4 s ?
d) Qual a velocidade instantânea em t = 4 s ?
e ) Qual a aceleração instantânea em t = 4s ?
f) Faça o gráfico a x t (aceleração versus tempo)
Resp. a) x(4s) = 12 m b) r(4s) = 12 m i; c) vmed = 7m/s i; d) v (4s) = 19,0 m/s; e) a (4s) = 16 m/s2; f) reta crescente.