Velocidade (Instantânea)

FAP151 - Fundamentos de Mecânica. Terceira Lista de exercícios. Março de 2009.
Velocidade (Instantânea)
Entregar as soluções dos exercícios 2 e 14, apresentando todas as etapas necessárias para
conseguir resolvê-los; não é suficiente apresentar as respostas.
Velocidade média
1) (RHK E2.6) A posição de um objeto que se move em linha reta é dada por x(t ) = At + Bt 2 + Ct 3 ,
onde A = 3,0 m/s, B = − 4,0 m/s2 e C = 1,0 m/s3.
a) Qual a posição do objeto nos instantes t = 0, 1, 2, 3 e 4 s?
b) Qual o deslocamento do objeto entre t = 0 e t = 2 s? E entre t = 0 e t = 4 s?
c) Qual a velocidade média no intervalo de tempo de t = 2 s a t = 4 s? E entre t = 0 e t = 3 s?
Representação gráfica do movimento: a velocidade é a inclinação da reta tangente
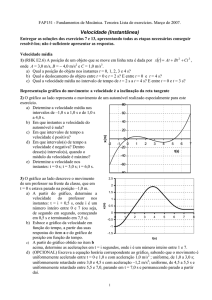
2) O gráfico ao lado representa o movimento de um automóvel subindo uma ladeira, em que o motorista
pára o carro, que escorrega um tanto para trás antes de retomar a subida.
a) Determine a velocidade média nos intervalos de –1,0 s a 1,0 s e de 1,0 s a 4,0 s.
b) Em que instantes a velocidade do automóvel
8
é nula?
x(m)
6
c) Qual a distância percorrida para trás pelo
automóvel, desde que ele pára a primeira vez
4
até que ele retome o movimento para cima da
2
ladeira?
d) Em que intervalos de tempo a velocidade é
0
t(s)
positiva?
-2
0
2
4
6
-2
e) Em que intervalo(s) de tempo a velocidade é
negativa? Dentro desse(s) intervalo(s),
-4
quando o módulo da velocidade é máximo?
-6
f) Determine a velocidade nos instantes: t = 0 s;
t = 3,0 s e t = 6,0 s.
-8
x(m)
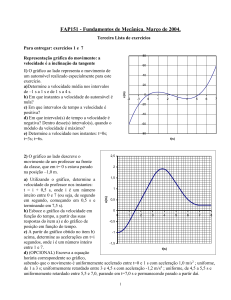
3) O gráfico ao lado descreve o movimento
2.5
de um professor na frente da classe, que em
2
t = 0 s estava parado na posição –1,0 m.
1.5
a) A partir do gráfico, determine a
velocidade do professor nos instantes:
1
ti = i + 0,5 s, onde i é um número
0.5
inteiro entre 0 e 7 (ou seja, de segundo
em segundo, começando em 0,5 s e
t(s)
0
terminando em 7,5 s).
1
2
3
4
5
6
7
8
-0.5 0
b) Esboce o gráfico da velocidade em
função do tempo, a partir das suas
-1
respostas do item a e do gráfico de
-1.5
posição em função do tempo.
c) A partir do gráfico obtido no item b acima, determine as acelerações em t = i segundos, onde i é
um número inteiro entre 1 e 7.
d) (OPCIONAL) Escreva a equação horária correspondente ao gráfico, sabendo que o movimento é
uniformemente acelerado entre t = 0 e 1,0 s com aceleração 1,0 m/s2 ; uniforme, de 1,0 a 3,0 s;
uniformemente retardado entre 3,0 e 4,5 s com aceleração −1,2 m/s2; uniforme, de 4,5 a 5,5 s e
uniformemente retardado entre 5,5 e 7,0 s, parando em t = 7,0 s e permanecendo parado a partir
daí.
1
4) Um minuto na vida de um velho passageiro de um velho ônibus.
“Eu me encaminho para o ponto do ônibus, distante 20 metros, andando 1 m/s. Olho para trás e vejo o
ônibus que, distante 50 metros do mesmo ponto, aproxima-se a 5 m/s. Resolvo correr para conseguir
chegar ao ponto antes do ônibus. O motorista percebe meu movimento, atenciosamente diminui sua
velocidade e pára no ponto alguns segundos depois de mim. Tomo o ônibus, encontro assento e o
ônibus acelera uniformemente de maneira que 5 segundos depois alcança 10 m/s e mantém essa
velocidade.” Represente num mesmo gráfico x vs. t os movimentos do velho senhor e do velho ônibus.
x(m)
t (s)
Dicas. O gráfico da posição em função do tempo de um movimento é contínuo−não tem saltos−e
quando não há colisão também é derivável−tem uma inclinação (velocidade) bem definida a cada
instante. Também preste atenção às velocidades do ônibus e do velho em t = 0 s, que são dados do
problema. Fora essas características, você tem liberdade – e obrigação – de escolher todos os detalhes
do problema que não tenham sido enunciados.
5) A vazão de um rio muda durante o ano de
acordo com o gráfico ao lado, onde o instante
t = 0 mês corresponde ao valor observado no
dia 1 de janeiro e há apenas um dado por mês.
Com base nesse gráfico:
a) determine a taxa de variação da vazão
(Tv) em unidades de (mil litros/s)/mês, no
período de janeiro a fevereiro, de fevereiro a
março e de junho a setembro;
b) represente graficamente o
comportamento da taxa de variação de vazão
ao longo do ano.
2
6) O gráfico abaixo representa o movimento da posição horizontal de um pêndulo em função do tempo.
6
x(cm)
4
2
t(s)
0
-2
-2
0
2
4
6
8
10
12
-4
-6
a) Esboce o gráfico da velocidade em função do tempo. Não se esqueça de marcar a escala e
identificar os eixos, incluindo as unidades.
b) A partir da sua resposta ao item a, esboce o gráfico da aceleração. Não se esqueça de marcar a
escala e identificar os eixos, incluindo as unidades.
7) O gráfico abaixo representa o movimento de um bloco preso a molas e apoiado sobre uma superfície
com atrito.
2
x(m)
1.5
1
0.5
0
-2
0
2
4
6
10 t(s)
8
-0.5
a) Esboce o gráfico da velocidade em função do tempo. Não se esqueça de marcar a escala e
identificar os eixos, incluindo as unidades.
b) A partir da sua resposta ao item a, esboce o gráfico da aceleração; é difícil ter boa precisão,
particularmente a partir de t = 4 s, de modo que se preocupe mais com os aspectos qualitativos da
aceleração que com os quantitativos. Apesar disso, não se esqueça de marcar a escala e
identificar os eixos, incluindo as unidades.
8) O gráfico abaixo representa o movimento de um corpo realizado especialmente para este exercício.
x(cm)
6
4
2
0
-6
-4
-2
0
2
4
t(s)
6
-2
a) Esboce o gráfico da velocidade em função do tempo. Não se esqueça de marcar a escala e
identificar os eixos, incluindo as unidades.
b) A partir da sua resposta ao item a, esboce o gráfico da aceleração. Não se esqueça de marcar a
escala e identificar os eixos, incluindo as unidades.
3
9) O gráfico abaixo representa o movimento de um balão de aniversário, com 20 cm de diâmetro e 20 g
de massa, abandonado de 2,0 m de altura e que rebate no chão.
y (m)
2
1.5
1
0.5
0
0
t(s)
0
0,2
0,4
0,6
0,7
0,8
1,0
1,2
1,4
v(m/s)
0.2
0.4
0.6
0.8
1
1.2
1.4 t (s)
a) Faça um esboço representando o sistema descrito no enunciado e marque
a origem e a orientação do eixo compatíveis com o gráfico.
b) Preencha a tabela de velocidade v em função do tempo t com valores
obtidos a partir do gráfico, por meio da inclinação da reta tangente à curva y(t) no
instante adequado.
c) Usando os dados da tabela, construa o gráfico da velocidade em função do
tempo: marque os pontos no gráfico (não se esqueça de marcar a escala e
identificar os eixos, incluindo as unidades) e una os pontos por uma curva suave,
exceto no instante em que a bola rebate no chão.
d) Determine a fração da energia cinética do balão que é perdida na rebatida
no chão.
e) Determine, a partir do gráfico v(t), em que instantes a aceleração é
máxima. Qual o valor máximo da aceleração, excetuando o valor no instante em
que a bola rebate no chão?
Equação horária do movimento
10) (RHK E2.20) Enquanto pensava em Isaac Newton, uma pessoa em pé sobre uma passarela
inadvertidamente deixa cair uma maçã por cima do parapeito justamente quando a frente de um
caminhão passa exatamente por baixo dele. O veículo move-se a 55 km/h e tem 12 m de comprimento.
A que altura, acima do caminhão, está o parapeito se a maçã passa rente à traseira do caminhão?
Representação algébrica do movimento: a velocidade é a derivada da função posição
11) Uma partícula move-se ao longo do eixo x de acordo com a equação x(t) = 50t + 2t3, sendo x em
centímetros e t em segundos. Calcule:
a) a velocidade média da partícula no intervalo [0 s, 3 s] do movimento;
b) a velocidade instantânea da partícula em t = 3,0 s e
c) a aceleração nesse mesmo instante.
4
12) A equação horária do movimento de um corpo é
x(t) = − 3 + 4t − 2t2 (x em metros para t em segundos).
a) Esboce o gráfico da posição x contra o tempo t no intervalo (-1; 3) s.
b) Qual é sua velocidade e sua aceleração instantânea como função do tempo?
c) Esboce os gráficos da velocidade, v, e da aceleração, a, em função do tempo no intervalo (-1; 3)
s.
d) Qual é a sua velocidade média no intervalo (-1; 2) s ?
e) No instante t = 0 s, um outro objeto, movendo-se uniformemente com rapidez |v| = 2,0 m/s no
sentido oposto ao do eixo Ox, cruza com o corpo cujo movimento está descrito no item a.
Escreva a equação horária do movimento deste outro objeto.
f) Em que instante posterior a t = 0 s os dois objetos voltam a se cruzar? E em que posição?
13) A posição de uma partícula ao longo do eixo x depende do tempo de acordo com a equação
x (t ) = At 2 − Bt 3 , onde x está em metros e t em segundos.
a) Em quais unidades do SI devem estar A e B?
A partir de agora admita que os valores numéricos de A e B, em unidades do SI, são 3,0 e 1,0,
respectivamente.
b) A partir de qual instante a partícula passa a ocupar posições na parte negativa do eixo Ox?
c) Qual o comprimento total da trajetória percorrida pela partícula nos primeiros 4,0 segundos?
d) Qual é o seu deslocamento durante os primeiros 4,0 segundos?
e) Qual a velocidade da partícula ao final de cada um dos quatro primeiros segundos?
f) Qual é a aceleração da partícula ao final de cada um dos quatro primeiros segundos?
g) Qual é a velocidade média para o intervalo de tempo compreendido entre t = 2,0 e t = 4,0 s?
14) (RHK E2.9) A posição de uma partícula que se move ao longo do eixo x é dada em cm por
x (t ) = A + Bt 3 , onde A = 9,75 cm e B = 1,50 cm/s3. Considere o intervalo de tempo de t = 2,00 s a
t = 3,00 s e calcule:
a) a velocidade média;
b) a velocidade instantânea em t = 2,00 s;
c) a velocidade instantânea em t = 3,00 s;
d) a velocidade instantânea em t = 2,50 s e
e) a velocidade instantânea quando a partícula estiver no ponto médio entre as posições ocupadas
nos instantes t = 2,00 s e t = 3,00 s.
15) (YF2.7, modificado) Um carro, que estava parado em um semáforo, inicia seu movimento no
instante escolhido como origem de tempo e percorre um trecho retilíneo de modo que sua distância ao
semáforo é dada por x(t ) = bt 2 − ct 3 , onde b = 2,40 m/s2 e c = 0,120 m/s3 .
a) Calcule a velocidade média do carro para o intervalo de tempo entre t = 0 e t = 10,0 s.
b) Calcule a velocidade instantânea do carro nos instantes t = 0; 5,0 e 10,0 s.
c) Usando uma planilha de cálculo, verifique numericamente que o instante em que o carro está no
ponto médio das posições ocupadas em t = 0 e t = 10,0 s é tm = 5,97 = 6,0 s com dois dígitos
significativos. Calcule a velocidade instantânea nesse ponto.
d) Qual o primeiro instante após t = 0 s em que o carro pára? E quando ele retorna à origem?
5