RELAÇÕES MÉTRICAS NUM TRIÂNGULO QUALQUER (32,3

RELAÇÕES MÉTRICAS NUM TRIÂNGULO
QUALQUER
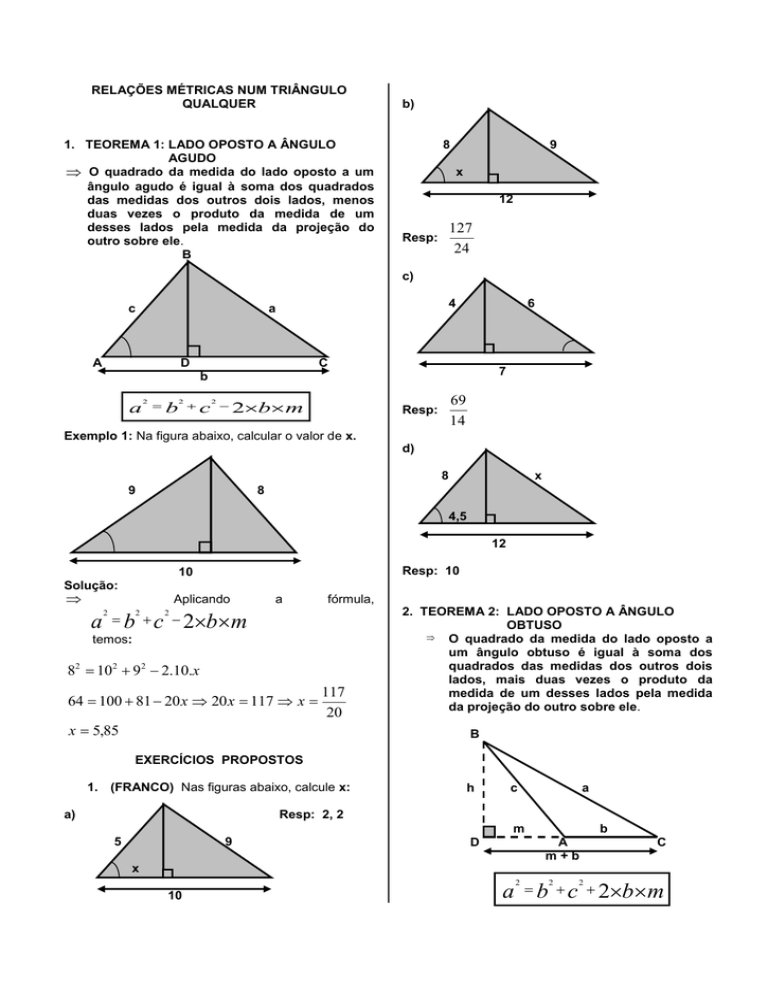
1. TEOREMA 1: LADO OPOSTO A ÂNGULO
AGUDO
 O quadrado da medida do lado oposto a um
ângulo agudo é igual à soma dos quadrados
das medidas dos outros dois lados, menos
duas vezes o produto da medida de um
desses lados pela medida da projeção do
outro sobre ele.
B
b)
8
9
x
12
127
24
Resp:
c)
c
h
4
a
m
6
x
b-m
A
D
C
7
b
a
2

b
2
 c  2b m
69
14
2
Resp:
Exemplo 1: Na figura abaixo, calcular o valor de x.
d)
8
9
x
8
4,5
12
x
Resp: 10
10
Solução:

Aplicando
a
fórmula,
a  b  c  2bm
2
2
2
temos:
82  102  92  2.10.x
64  100  81  20 x  20 x  117  x 
117
20
x  5,85
2. TEOREMA 2: LADO OPOSTO A ÂNGULO
OBTUSO
 O quadrado da medida do lado oposto a
um ângulo obtuso é igual à soma dos
quadrados das medidas dos outros dois
lados, mais duas vezes o produto da
medida de um desses lados pela medida
da projeção do outro sobre ele.
B
EXERCÍCIOS PROPOSTOS
1. (FRANCO) Nas figuras abaixo, calcule x:
a)
h
c
a
Resp: 2, 2
m
5
9
D
b
A
m+b
C
x
a  b  c  2bm
2
10
2
2
Exemplo 1: Na figura abaixo, calcular o valor de x.
3
10
Resp: 14
e)
14
6
x
3
x
10
1,5
Solução:
5
Resp: 7

Aplicando
a
fórmula,
a  b  c  2b m
2
2
2
temos:
14 2  10 2  6 2  2.10.x
196  100  36  20 x  20 x  196  36 
60
 20 x  60  x 
 x3
20
EXERCÍCIOS PROPOSTOS
1. (FRANCO) Nas figuras abaixo, calcule x:
a)
Resp: 4, 4
13
10
x
3. NATUREZA DE UM TRIÂNGULO:
 Podemos estabelecer o seguinte critério para
classificar triângulos quanto aos ângulos:
 Sendo a a medida do maior lado, temos:
a 2  b 2  c 2  Triângulo Re tângulo
 2
2
2
a  b  c  Triângulo Acutângulo
a 2  b 2  c 2  Triângulo Obtusângulo

Exemplos:
Ex1: Um triângulo cujos lados medem 3 cm, 4 cm e
5 cm é Retângulo:
52  32  42

Justificando  25  9  16
25  25

5
b)
Ex2: Um triângulo cujos lados medem 4 cm, 5 cm e
6 cm é Acutângulo:
8
4
5
x
Resp: 2, 3
c)
Ex3: Um triângulo cujos lados medem 4 cm, 2 cm e
5 cm é Obtusângulo:
x
8
2
10
2 51
d)
62  42  52

Justificando  36  16  25
36  41

Resp:
52  42  22

Justificando  25  16  4
25  20

T E S T E S
x
6
1. (FRANCO) O triângulo cujos lados medem 5 cm,
12 cm e 13 cm:
a)
b)
c)
d)
é acutângulo
é retângulo
é obtusângulo
não existe
8. (FRANCO) O perímetro do triângulo EFG da
figura é:
2. (FRANCO) O triângulo cujos lados medem 11 cm,
6 cm e 9 cm:
a)
b)
c)
d)
é acutângulo
é retângulo
é obtusângulo
não existe
a)
b)
c)
d)
32
36
38
40
x
10
3. (FRANCO) O triângulo cujos lados medem 8 cm,
15 cm e 17 cm:
a)
b)
c)
d)
um ângulo reto
dois ângulos retos
três ângulos retos
um ângulo obtuso
4. (FRANCO) Com três segmentos e comprimentos
iguais a 10 cm, 12 cm e 23 cm...
a) é possível formar
apenas um triângulo
retângulo
b) é possível formar apenas um
triângulo
obtusângulo.
c) é possível formar apenas um triângulo
acutângulo.
d) não é possível formar um triângulo.
5. (FRANCO) No triângulo da figura abaixo, o valor
de x é:
a)
b)
c)
d)
6
7
8
9
x
5
3,8
10
6. (FRANCO) No triângulo da figura abaixo, o valor
de x é:
a)
b)
c)
d)
7.
a)
b)
c)
d)
7
8
9
10
(FRANCO)
figura é:
22
23
24
25
5
x
1
4
O perímetro do triângulo ABC da
x
5
2,2
10
12
4
G A B A R I T O
1. B
6. A
2. C
7. C
3. A
8. D
4. D
5. B