COOPEN – Cooperativa de Ensino de Rio Verde Ltda

Data
___/___/2017
Série:
Turma: U
Professor:
Estudante:
DNA - Sistema Hércules de Educação
[email protected]
Disciplina:
Lista do Dia
1. Ao se discutirem as ideias expostas na assembleia, chegou-se à seguinte conclusão: pôr em confronto
essas ideias com outras menos polêmicas seria avaliar melhor o peso dessas ideias, à luz do princípio
geral que vem regendo as mesmas ideias.
a) Transcreva o texto, substituindo as expressões sublinhadas por pronomes pessoais que lhes sejam
correspondentes e efetuando as alterações necessárias.
b) Reescreva a oração Ao se discutirem as ideias expostas na assembleia, introduzindo-a pela conjunção
adequada e mantendo a correlação entre os tempos verbais.
2. Cultivar amizades, semear empregos e preservar a cultura fazem parte da nossa natureza.
a) Explique o efeito expressivo que, por meio da seleção lexical, se obteve nesta frase.
b) Reescreva a frase, substituindo por substantivos cognatos os verbos cultivar, semear e preservar,
fazendo também as adaptações necessárias.
3. Orientação para uso deste medicamento: antes de você usar este medicamento, verifica se o rótulo
consta as seguintes informações, seu nome, nome de seu médico, data de manipulação e validade e
fórmula do medicamento solicitado.
a) Há no texto desvios em relação à norma culta. Reescreva-o, fazendo as correções necessárias.
b) A que se refere, no contexto, o pronome seu da expressão “seu nome”? Justifique sua resposta.
4. Leia com atenção os versos finais do poema “Jardim da Praça da Liberdade”, de Carlos Drummond de
Andrade:
De repente uma banda preta
vermelha retinta suando
bate um dobrado batuta
na doçura
do jardim.
Repuxos espavoridos fugindo.
a) Identifique um dos recursos sonoros empregados nestes versos, explicando qual é o efeito expressivo
obtido.
b) Interprete o último verso do poema, indicando o sentido da palavra “repuxos” e explicando por que
os repuxos estão “espavoridos fugindo”.
5. Ouvir alguém falar não é como tornar a ouvi-lo através de uma máquina: o que ouvimos, quando
temos um rosto diante de nós, nunca é o que ouvimos, quando, diante de nós, há uma fita que gira. Um
reluzir de olhos, um agitar de mãos, às vezes, torna aceitável a frase mais idiota. Mas sem aquelas mãos,
sem aqueles olhos, a frase se desnuda em toda a sua desconcertante idiotice.
Para quem faz DNA, a seleção é natural!
(Oriana Fallaci. Os antipáticos)
a) Complete, mantendo o sentido do texto, o segmento A frase mais idiota torna-se, às vezes, aceitável,
a não ser que .......
b) Termine a frase A presença física de nosso interlocutor ...... com uma conclusão que sintetize o texto.
6. Um número inteiro positivo n de 4 algarismos decimais satisfaz às seguintes condições:
I) a soma dos quadrados dos 1º e 4º algarismos é 58;
II) a soma dos quadrados dos 2º e 3º algarismos é 52;
III) se deste número n subtrairmos o número 3816,
obteremos um número formado pelos mesmos algarismos do número n, mas na ordem contrária. Qual
é esse número?
7. Um comerciante compra calças, camisas e saias e as revende com lucro de 20%, 40% e 30%
respectivamente. O preço x que o comerciante paga por uma calça é três vezes o que ele paga por uma
camisa e duas vezes o que ele paga por uma saia. Um certo dia, um cliente comprou duas calças, duas
camisas e duas saias e obteve um desconto de 10% sobre o preço total.
a) Quanto esse cliente pagou por sua compra, em função de x?
b) Qual o lucro aproximado, em porcentagem, obtido pelo comerciante nessa venda?
8. Uma função f satisfaz a identidade f(ax) = af(x) para todos os números reais a e x. Além disso, sabe-se
que f(4) = 2. Considere ainda a função g(x)= f(x-1)+1 para todo o número real x.
a) Calcule g(3).
b) Determine f(x), para todo x real.
c) Resolva a equação g(x) = 8
9. A reta s passa pela origem O e pelo ponto A do primeiro quadrante. A reta r é perpendicular à reta s,
no ponto A, e intercepta o eixo x no ponto B e o eixo y no ponto C. Determine o coeficiente angular de s
se a área do triângulo OBC for o triplo da área do triângulo OAB.
10. No paralelogramo ABCD abaixo, tem-se que AD = 3 e
pertence ao lado
e à bissetriz do ângulo
.
a) Calcule AP
b) Determine AB sabendo que a área do quadrilátero ABCP é 21.
. Além disso, sabe-se que o ponto P
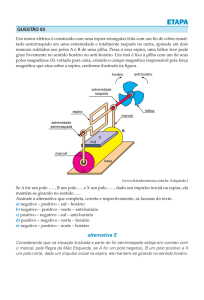
11. Um procedimento para estimar o campo magnético de um ímã baseia-se no movimento de uma
grande espira condutora E através desse campo. A espira retangular E é abandonada à ação da
gravidade entre os polos do ímã de modo que, enquanto a espira cai, um de seus lados horizontais
(apenas um) corta perpendicularmente as linhas de campo. A corrente elétrica induzida na espira gera
uma força eletromagnética que se opõe a seu movimento de queda, de tal forma que a espira termina
atingindo uma velocidade V constante. Essa velocidade é mantida enquanto esse lado da espira estiver
passando entre os polos do ímã. A figura representa a configuração usada para medir o campo
magnético, uniforme e horizontal, criado entre os polos do ímã. As características da espira e do ímã
estão apresentadas na tabela. Para a situação em que um dos lados da espira alcança a velocidade
constante V = 0,40 m/s entre os polos do ímã, determine:
Para quem faz DNA, a seleção é natural!
ATENÇÃO: Desconsidere o campo magnético da Terra.
a) A intensidade da força eletromagnética F, em N, que age sobre a espira, de massa M, opondo-se à
gravidade no seu movimento de queda a velocidade constante.
b) O trabalho realizado pela força de gravidade por unidade de tempo (potência), que é igual à potência
P dissipada na espira, em watts.
c) A intensidade da corrente elétrica i, em amperes, que percorre a espira, de resistência R.
d) O campo magnético B, em tesla, existente entre os polos do ímã.
12. A relação entre tensão e corrente de uma lâmpada L, como a usada em automóveis, foi obtida por
meio do circuito esquematizado na figura 1, onde G representa um gerador de tensão variável. Foi
medido o valor da corrente indicado pelo amperímetro A, para diferentes valores da tensão medida
pelo voltímetro V, conforme representado pela curva L no Gráfico 1. O circuito da figura 1 é, então,
modificado, acrescentando-se um resistor R de resistência 6,0 Ω em série com a lâmpada L, conforme
esquematizado na figura 2.
a) Construa, no Gráfico 2, o gráfico da potência dissipada na lâmpada, em função da tensão U entre seus
terminais, para U variando desde 0 até 12 V.
b) Construa, no Gráfico 1 da folha de resposta, o gráfico da corrente no resistor R em função da tensão
U aplicada em seus terminais, para U variando desde 0 até 12 V.
Para quem faz DNA, a seleção é natural!
c) Considerando o circuito da figura 2, construa, no Gráfico 3 , o gráfico da corrente indicada pelo
amperímetro em função da tensão U indicada pelo voltímetro, quando a corrente varia desde 0 até 2 A.
13. Uma pequena esfera, com carga elétrica positiva Q = 1,5 x 10 -9 C, está a uma altura D = 0,05 m
acima da superfície de uma grande placa condutora, ligada à Terra, induzindo sobre essa superfície
cargas negativas, como na figura 1. O conjunto dessas cargas estabelece um campo elétrico que é
idêntico, apenas na parte do espaço acima da placa, ao campo gerado por uma carga +Q e uma carga Q, como se fosse uma “imagem” de Q que estivesse colocada na posição representada na figura 2.
ATENÇÃO: 1 N/C= 1 V/m
a) Determine a intensidade da força F, em N, que age sobre a carga +Q, devida às cargas induzidas na
placa.
b) Determine a intensidade do campo elétrico E0, em V/m, que as cargas negativas induzidas na placa
criam no ponto onde se encontra a carga +Q.
c) Represente, no diagrama, no ponto A, os vetores campo elétrico E+ e E−, causados, respectivamente,
pela carga +Q e pelas cargas induzidas na placa, bem como o campo resultante, EA. O ponto A está a
uma distância D do ponto O da figura e muito próximo à placa, mas acima dela.
d) Determine a intensidade do campo elétrico resultante EA, em V/m, no ponto A.
Para quem faz DNA, a seleção é natural!
14. Um jogador de futebol deve bater uma falta. A bola deverá ultrapassar a barreira formada 10 m à
sua frente. Despreze efeitos de resistência do ar e das dimensões da bola. Considere um ângulo de
lançamento de 45°, g = 10 m/s2, e uma velocidade inicial de lançamento v0 = 5√5 m/s. Determine qual é
a altura máxima dos jogadores da barreira para que a bola a ultrapasse.
15. Acredita-se que desde o século XIV acrobatas chineses já usavam uma versão primitiva do
paraquedas. É certo que, no ocidente, Leonardo da Vinci (1452-1519) já o havia imaginado. Essa bela
invenção utiliza um princípio físico muito simples: a força de resistência do ar ao movimento de um
corpo aumenta com o módulo de sua velocidade, bem como com a área transversal à direção de
movimento do paraquedas. Assim, após algum tempo, essa força se iguala à força-peso do conjunto
(paraquedista e paraquedas), de tal forma que, a partir desse momento, sua velocidade se torna
constante, a chamada velocidade limite. No caso de um salto livre, com o paraquedas fechado, atinge-se
a velocidade limite de, aproximadamente, 40 m/s depois de uma queda de cerca de 400 m. Já com ele
aberto, esses valores são, respectivamente, 5 m/s e 3 m. Calcule a aceleração média no primeiro caso
(paraquedas fechado), supondo que a velocidade inicial do corpo em queda seja nula. Supondo que a
altura inicial do salto seja de 800 m, calcule qual seria o tempo de queda até chegar ao solo após atingir
a velocidade limite no segundo caso (paraquedas aberto).
DESAFIO: Discorra sobre as palavras destacadas em negrito ao longo da sexta aberta.
Para quem faz DNA, a seleção é natural!