Lançamento oblíquo

Mecânica
(Professor: Sidclei)
Lançamento horizontal e lançamento oblíquo
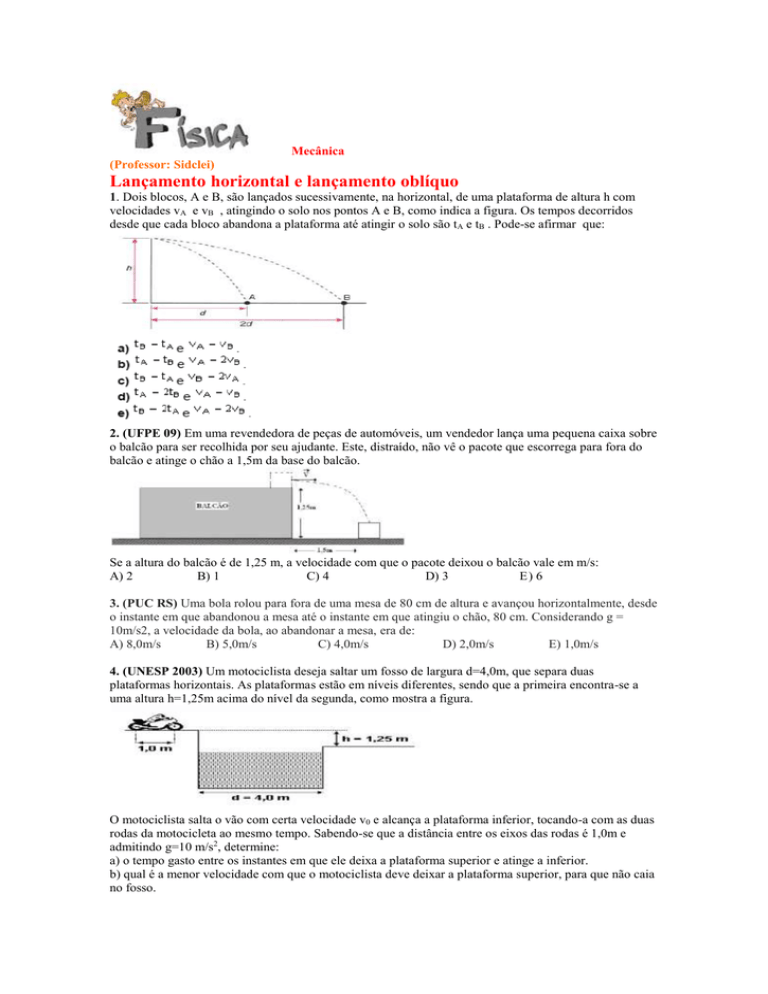
1. Dois blocos, A e B, são lançados sucessivamente, na horizontal, de uma plataforma de altura h com
velocidades vA e vB , atingindo o solo nos pontos A e B, como indica a figura. Os tempos decorridos
desde que cada bloco abandona a plataforma até atingir o solo são tA e tB . Pode-se afirmar que:
2. (UFPE 09) Em uma revendedora de peças de automóveis, um vendedor lança uma pequena caixa sobre
o balcão para ser recolhida por seu ajudante. Este, distraído, não vê o pacote que escorrega para fora do
balcão e atinge o chão a 1,5m da base do balcão.
Se a altura do balcão é de 1,25 m, a velocidade com que o pacote deixou o balcão vale em m/s:
A) 2
B) 1
C) 4
D) 3
E) 6
3. (PUC RS) Uma bola rolou para fora de uma mesa de 80 cm de altura e avançou horizontalmente, desde
o instante em que abandonou a mesa até o instante em que atingiu o chão, 80 cm. Considerando g =
10m/s2, a velocidade da bola, ao abandonar a mesa, era de:
A) 8,0m/s
B) 5,0m/s
C) 4,0m/s
D) 2,0m/s
E) 1,0m/s
4. (UNESP 2003) Um motociclista deseja saltar um fosso de largura d=4,0m, que separa duas
plataformas horizontais. As plataformas estão em níveis diferentes, sendo que a primeira encontra-se a
uma altura h=1,25m acima do nível da segunda, como mostra a figura.
O motociclista salta o vão com certa velocidade v0 e alcança a plataforma inferior, tocando-a com as duas
rodas da motocicleta ao mesmo tempo. Sabendo-se que a distância entre os eixos das rodas é 1,0m e
admitindo g=10 m/s2, determine:
a) o tempo gasto entre os instantes em que ele deixa a plataforma superior e atinge a inferior.
b) qual é a menor velocidade com que o motociclista deve deixar a plataforma superior, para que não caia
no fosso.
5. (UEMA) Imagine-se em um barranco de 5 m acima de um lago de 4 m de largura infestado de
piranhas. Para você não ser devorado pelas piranhas, qual deve ser a velocidade horizontal necessária para
pular o lago? Admitindo g =10 m/s2
a) 4 m/s.
b) 2 m/s.
c) 5 m/s.
d) 3 m/s.
e) 6 m/s.
6. (UNESP 2005) Um balão se desloca horizontalmente, a 80,0 m do solo, com velocidade constante de
6,0 m/s. Quando passa exatamente sobre um jovem parado no solo, um saquinho de areia é abandonado
do balão. Desprezando qualquer atrito do saquinho com o ar e considerando g = 10,0 m/s2, calcule:
a) o tempo gasto pelo saquinho para atingir o solo, considerado plano.
b) a distância entre o jovem e o ponto onde o saquinho atinge o solo.
7. (FUVEST-SP) Num jogo de vôlei, o jogador que está junto à rede salta e "corta" uma bola levantada
na direção vertical, no instante em que ela atinge sua altura máxima, h = 3,2 m.
Nessa "cortada", a bola adquire uma velocidade de módulo V, na direção paralela ao solo e perpendicular
à rede, e cai exatamente na linha de fundo da quadra.
A distância entre a linha de meio da quadra (projeção da rede) e a linha de fundo é d = 9,0 m.
Adote g = 10m/s2e despreze o efeito do ar.
Calcule:
a) O tempo decorrido entre a cortada e a queda da bola na linha de fundo.
b) O módulo V da velocidade que o jogador transmitiu à bola.
8. (UERJ 09) Um avião, em trajetória retilínea paralela à superfície horizontal do solo, sobrevoa uma
região com velocidade constante igual a 360 km/h. Três pequenas caixas são largadas, com velocidade
inicial nula, de um compartimento na base do avião, uma a uma, a intervalos regulares iguais a 1 segundo.
Desprezando-se os efeitos do ar no movimento de queda das caixas, determine as distâncias entre os
respectivos pontos de impacto das caixas no solo.
9. (UEM 08) Um projétil é lançado horizontalmente do alto de um rochedo de 490,0 m de altura, com
uma velocidade inicial de 30,0 m/s. Considere g = 9,8 m/s 2 e assinale o que for correto.
(01) O projétil alcança o solo a uma distância horizontal de 580,0 m de seu ponto de lançamento.
(02) No eixo x, o objeto descreve um movimento retilíneo uniforme, com a = 0,0 m/s2, e, no eixo y, um
movimento retilíneo uniformemente variado, com uma aceleração de 9,8 m/s2, na direção vertical e no
sentido de cima para baixo.
(04) Em t = 5,0 s, o objeto encontra-se nas coordenadas x = 150,0 m e y = 367,5 m.
(08) Em t = 5,0 s, o objeto possui uma velocidade vertical de módulo 30,0 m/s.
(16) Após o lançamento, o objeto alcança o solo em t = 30,0 s
10. (AFA) Um avião voando a 400 metros de altura em relação ao solo, com velocidade de 100m/s, lança
uma bomba que atinge um alvo no topo de uma colina, a 155 metros de altura, também em relação ao
solo. O tempo, em segundos, entre o lançamento e o impacto da bomba, e a distância, em metros, entre o
avião e o alvo, no instante do lançamento, são respectivamente:
a) 4 e 400
b) 7 e 700
c) 8 e 800
d) 10 e 1000
11) Um estudante está parado sobre a beira de um precipício e chuta uma pedra horizontalmente com uma
velocidade de 18,0m/s. O precipício está 50m acima de uma praia plana, como ilustrado na figura abaixo.
Responda:
a) Quanto tempo após ter sido liberada a pedra atinge a praia abaixo do precipício?
b)Qual é a magnitude da velocidade e o ângulo de impacto da pedra?
12- (UFCG PB/2007) Num certo momento, no faroeste Justiça Selvagem de 1933, John Wayne está
prestes a saltar sobre um fora-da-lei espreitando-o sobre uma árvore. A altura do herói, medida
verticalmente, em relação à sela do cavalo, que se move em movimento retilíneo uniforme com
velocidade de 10 m/s, é de 3,2m.
O herói conseguiu deter o fora-da-lei. Considerando que sobre ele atuou, durante todo o tempo da queda,
somente a força peso, pode-se afirmar que,
a) o tempo de queda do herói foi de 0,32s.
b) o herói pulou quando o cavalo estava a uma distância de sua posição, medida horizontalmente, de
8,0m.
c) quando o cavalo estava exatamente abaixo do herói ele pulou gastando 0,80s para atingir o fora-da-lei.
d) desde o instante em que o herói pulou e o instante em que atingiu o fora-da-lei, o cavalo percorreu uma
distância igual a 6,4m.
e) ao atingir o fora-da-lei, a velocidade do herói foi de 4,0m/s.
13 - (FFFCMPA RS/2007) Uma pedra é arremessada horizontalmente, com uma velocidade de 20m/s,
de uma ponte que está a 16m acima da superfície da água. Qual a velocidade da pedra, após atingir a
água? (Considere g = 9,8m/s2)
a) 26,7m/s.
b) 13,5m/s.
c) 713,6m/s.
d) 42,5m/s.
e) 246,4m/s.
14 - (UFV MG/2007) Um projétil é lançado horizontalmente de uma altura de 20 m, com uma velocidade
inicial de módulo igual a 15 m/s. Desprezando-se a resistência do ar e considerando o módulo da
aceleração gravitacional como 10 m/s2, é CORRETO afirmar que o projétil atingirá o solo após ter
percorrido uma distância horizontal igual a:
a) 11 m
b) 15 m
c) 60 m
d) 23 m
e) 30 m
15. (PUC-SP) O esquema apresenta uma correia que transporta minério, lançando-o no recipiente R.
A velocidade da correia é constante. Para que todo o minério caia dentro do recipiente, a velocidade v da
correia, dada em m/s, deve satisfazer a desigualdade:
a) 2<v<3
b) 2<v<5
c) 1<v<3
d) 1<v<4
e) 1<v<5
Lançamento oblíquo
16. Um projétil é lançado com velocidade de 100 m/s segundo um ângulo de 53º com a horizontal.
Considere sen 53º = 0,8 e cos 53º = 0,6. Calcule:
a) a componente horizontal e vertical da velocidade no início do movimento;
b) o tempo de subida;
c) a altura máxima atingida pelo projétil;
d) o alcance do projétil
17. Ao bater um tiro de meta, um goleiro imprime à bola uma velocidade de módulo v 0 = 25 m/s inclinada
de um ângulo θ com a horizontal, tal que sen θ = 0,8 e cos θ = 0,6. Admita que no local a resistência do ar
seja desprezível e adote g = 10 m/s2.
Supondo que a bola retorne ao solo sem ser interceptada por qualquer jogador, determine:
a) a altura máxima (H) atingida por ela;
b) a velocidade da bola no ápice do vôo;
c) o seu tempo total de vôo (T)
d) o seu alcance horizontal (D).
18. Um gato, de um quilo, dá um pulo, atingindo uma altura de 1,25m e caindo a uma distância de 1,5m
do local do pulo.
a) Calcule a componente vertical de sua velocidade inicial.
b) Calcule a velocidade horizontal do gato.
c) Qual a força que atua sobre o gato no ponto mais alto do pulo?
19. Um menino, andando de "skate" com velocidade v=2,5m/s num plano horizontal, lança para cima
uma bolinha de gude com velocidade vo=4,0m/s e a apanha de volta.
Considere g=10m/s2
a) Esboce a trajetória descrita pela bolinha em relação à Terra.
b) Qual é a altura máxima que a bolinha atinge?
c) Que distância horizontal a bolinha percorre?
20-(UNICAMP–SP) Até os experimentos de Galileu Galilei pensavam-se que, quando um projétil era
arremessado, o seu movimento devia-se ao impetus, o qual mantinha o projétil em linha reta e com
velocidade constante. Quando o impetus acabasse, o projétil cairia verticalmente até atingir o chão.
Galileu demonstrou que a noção de impetus era equivocada.
Consideremos que um canhão dispara projéteis com uma velocidade inicial de 100 m/s, fazendo um
ângulo de 30º com a horizontal. Dois artilheiros calcularam a trajetória de um projétil: um deles,
Simplício, utilizou a noção de impetus; o outro, Salviati, as idéias de Galileu. Os dois artilheiros
concordavam apenas em uma coisa: o alcance do projétil.
Considere √3 =1,8; sen 30º = 0,5; cos 30º = 0,9.
Despreze a resistência do ar.
a) Qual é o alcance do projétil?
b) Qual é a altura máxima alcançada pelo projétil, segundo os cálculos de Simplício?
c) Qual é a altura máxima alcançada pelo projétil, calculada por Salviati?
21. Uma catapulta (arma medieval utilizada para lançar objetos) arremessa uma pedra de 60 kg com uma
velocidade de 20 m/s, num ângulo de 60º com o solo. Sabendo que a catapulta está a 20 m da muralha do
castelo que vai ser atacado e a muralha tem 12 m de altura, calcule se a pedra vai bater contra a muralha
ou cair dentro do pátio do castelo.
22. Um bombeiro, combatendo um incêndio, dirige o jato de água de uma mangueira com um ângulo de
30º com a horizontal. Se a velocidade da corrente de água for 40 m/s, no bico da mangueira, e se o
edifício em fogo estiver a 50 m de distância, até que andar aproximadamente poderá ser alcançado pela
água. Considere que cada andar tenha em média 3,0 m.
23. (UFJF-MG) Durante uma partida de futebol, um jogador, percebendo que o goleiro do time
adversário está longe do gol, resolve tentar um chute de longa distância (vide figura). O jogador se
encontra a 40 m do goleiro. O vetor velocidade inicial da bola tem módulo Vo = 26 m/s e faz um ângulo
de 25° com a horizontal, como mostra a figura a seguir.
Desprezando a resistência do ar, considerando a bola pontual e usando cos 25° = 0,91, sen 25° = 0,42 e
g =10m/s2:
a) Faça o diagrama de forças sobre a bola num ponto qualquer da trajetória durante o seu vôo, após ter
sido chutada. Identifique a(s) força(s).
b) Saltando com os braços esticados, o goleiro pode atingir a altura de 3,0 m. Ele consegue tocar a bola
quando ela passa sobre ele? Justifique.
c) Se a bola passar pelo goleiro, ela atravessará a linha de gol a uma altura de 1,5 m do chão. A que
distância o jogador se encontrava da linha de gol, quando chutou a bola? (Nota: a linha de gol está atrás
do goleiro.)
24. (UNICAMP-SP) Uma bola de tênis rebatida numa das extremidades da quadra descreve a trajetória
representada na figura a seguir, atingindo o chão na outra extremidade da quadra. O comprimento da
quadra é de 24 m.
a) Calcule o tempo de vôo da bola, antes de atingir o chão. Desconsidere a resistência do ar nesse caso.
b) Qual é a velocidade horizontal da bola no caso acima?
c) Quando a bola é rebatida com efeito, aparece uma força, FE, vertical, de cima para baixo e igual a 3
vezes o peso da bola. Qual será a velocidade horizontal da bola, rebatida com efeito para uma trajetória
idêntica à da figura?
25. Em um local onde o efeito do ar é desprezível e g =10m/s 2, uma bola de tênis é golpeada adquirindo
uma velocidade de módulo 10m/s quando estava a uma altura de 1,0m acima do chão. A altura máxima
atingida pela bola, medida a partir do chão, foi de 4,75m. Determine o módulo da velocidade da bola no
ponto mais alto de sua trajetória.
26. (UNICAMP-SP) O famoso salto duplo twistcarpado de Daiane dos Santos foi analisado durante um
dia de treinamento no Centro Olímpico em Curitiba, através de sensores e filmagens que permitiram
reproduzir a trajetória do centro de gravidade de Daiane na direção vertical (em metros), assim como o
tempo de duração do salto.
De acordo com o gráfico, determine:
a) A altura máxima atingida pelo centro de gravidade de Daiane.
b) A velocidade média horizontal do salto, sabendo-se que a distância percorrida nessa direção é de 1,3m.
c) A velocidade vertical de saída do solo.
27. (UDESC-SC-2009) Em uma partida de basquete, um jogador tem direito a realizar dois lances livres.
O centro da cesta está situado a uma distância de 4,0 m da linha de lançamento e a uma altura de 3,0 m do
solo, conforme a figura abaixo. A bola é lançada sempre a uma altura de 2,0 m do solo.
No primeiro lançamento, a bola é lançada com velocidade de 5,0 m/s, formando um ângulo de 30° com a
horizontal, e não atinge a cesta. No segundo lançamento, a bola é lançada com uma velocidade
desconhecida, formando um ângulo de 30° com a horizontal, e atinge a cesta.
Dados: cos 30° = 0,86; sen 30° = 0,50; tan 30° = 0,57; cos2 30° = 0,75.
a) Determine o instante em que a altura máxima é atingida pela bola no primeiro lançamento.
b) Demonstre que a bola não atinge a cesta no primeiro lançamento.
c) Determine a velocidade inicial da bola no segundo lançamento
28. Do alto de uma torre de 20m de altura, um artilheiro mira um balão que se encontra parado sobre um
ponto situado a 400m do pé da torre. O ângulo de visão do artilheiro em relação à horizontal é de 15o. No
instante exato em que o artilheiro dispara um projétil (P) os ocupantes do balão deixam cair um objeto
(O), que é atingido pelo disparo. A velocidade do projétil ao deixar o cano da arma é vo = 200m/s.
Despreze a resistência do ar e adote g = 9,8m/s2, sen15o = 0,26 e cos15o = 0,97.
a) Calcule o instante do encontro projétil-objeto;
b) Calcule a altura em que acontece o encontro.
29. O salto que conferiu a medalha de ouro a uma atleta brasileira, na Olimpíada de 2008, está
representado no esquema abaixo, reconstruído a partir de fotografias múltiplas.
Nessa representação, está indicada, também, em linha tracejada, a trajetória do centro de massa da atleta.
Utilizando a escala estabelecida pelo comprimento do salto, de 7,04 m, é possível estimar que o centro de
massa da atleta atingiu uma altura máxima de 1,25 m (acima de sua altura inicial), e que isso ocorreu a
uma distância de 3,0 m na horizontal, a partir do início do salto, como indicado na figura. Considerando
essas informações, estime.
a) O intervalo de t1 em s, entre o instante do início do salto e o instante em que o centro de massa da atleta
atingiu sua altura máxima.
b) A velocidade horizontal média, VH, em m/s, da atleta durante o salto.
c) O intervalo de tempo t2, em s, entre o instante em que a atleta atingiu sua altura máxima e o instante
final do salto.
Gabarito:
1.c
2.d
7.a)0,8s
3.d
b)11,25m/s
11.a) 35,8m/s
4. a)0,5s
b)10m/s
8. 100m
b) 600 em relação á horizontal
16. a) v0x = 60m/s e v0y = 80m/s
b) ts = 8s
17. a) H máx. = 20m
b) v0x = 15m/s
18. a) v0y = 5,0m/s
b) v0x = 1,5 m/s
c) tT = 4s
5.a
9. V (02,04)
12.b
13. a
6. a)4s
b)24m
10) b
14. e
15. d
c)H máx. = 320m d) D = 960m
d) D = 60m
c) P = 10N
19. a) a trajetória é uma parábola b) H máx. = 0,8m c) D = 2m
20. a) D = 960m
b) H máx. = 540m c) H máx. = 125m
21. A pedra vai cair dentro do pátio do castelo, pois ao passar pelo muro em t = 2s ela estará a uma
altura de 14m.
22. 6º andar
23. a) a) A única força que age sobre a bola (a resistência do ar é desprezada) durante todo o
movimento é a força peso, vertical e para baixo.
b) não, quando a bola passa por ele no instante t= 1,69s ela estará a uma altura de h =4,17m
c) considera-se o tempo maior que ocorre quando a bola já está descendo t = 2,042s , nesse instante
a distância horizontal da linha de gol será de D=48,3m.