39 e 40.

ORIENTADOR(A) : LEANDRO ◊ TURNO: Noite ◊ ( S a l a 6 )
DISCIPLINA:MATEMÁT ICA ◊ A U L A S : 3 9 e 4 0 ◊ DATA:23/05/2010
PAUTA DO DIA:
* Apresentação dos grupos: Síntese – Resumo da aula anterior; Coordenação – Pauta do dia;
*Sugestão de dinâmica: Socialização;
PAUTA DO DIA
*APRESENTÇÃO DAS EQUIPES
*PROBLEMATIZAÇÃO
*VIDEO AULA 39
*LEITURA DE IMAGEM
*ATIVIDADES
*VÍDEO AULA – 40
*LEITURA DE IMAGEM
*ATIVIDADES EM GRUPO
*EXERCÍCIOS DO LIVRO
*MEMORIAL
*AVALIAÇÃO
AULA 39 – MEDIDAS DE ÂNGULOS
( É NECESSÁRIO O USO DE TRANSFERIDOR NESSA SALA )
Problematizações :
1) Peça aos alunos que escreva no caderno 5 (cinco) situações onde encontramos ângulos,
em seguida eles devem socializar as respostas..
2) Pergunte a eles o que é um angulo reto, agudo e obtuso .
Resposta : Reto = 90º / obtuso = maior que 90º / agudo =
menor que 90º
3) Desenhe um relógio marcando 2 horas e em seguida
pergunte aos alunos :
Quantos ângulos os ponteiros podem formar ? Resp : 2 Ângulos
Qual é oa medida do menor ângulo formado pelos ponteiros
dorelógio ?
360
= 30
30 x 2 = 60º
12
Vídeo aula 29
Leitura de imagens
Qual instrumento serve para medir um ângulo ? Resp : Transferidor
Para se formar um angulo, o que é necessário ? Resp : Dois segmentos de reta consecutivos.
Em que profissões é secessário se conhecer angulos ? Resp: Engenheiro, arquiteto, pedreiro,
marinheiros e etc.
Como se forma um ângulo ? Resp : Através de um vértice, formado por dois segmentos de
reta
Ângulo é a região de um plano concebida pela abertura de duas semi-retas que possuem uma
origem em comum, chamada vértice do ângulo. A abertura do ângulo é uma propriedade invariante e
é medida em radianos ou graus.
Componentes de um ângulo


Semi-retas - são as duas retas laterais ao ângulo.
Origem ou vértice - ponto onde as duas semi-retas se cruzam.
Ângulo agudo
Ângulo reto
Ângulo obtuso
Ângulo raso
Quanto a complementação

Ângulos Complementares - Dois ângulos são Complementares quando a soma de suas
medidas é igual a 90°. Neste caso, cada um é o complemento do outro.

Ângulos Suplementares - Dois ângulos são Suplementares quando a soma de suas
medidas é igual a 180°. Neste caso, cada um é o suplemento do outro.

Ângulos Replementares - Dois ângulos são Replementares quando a soma de suas
medidas é igual a 360°. Neste caso, cada um é o replemento do outro.

Complemento de x Suplemento de x Replemento de x
90º - x
180º - x
360º - x
Atividade do livro 1 de matemática . Páginas 37 e 38.
Obs : Todos podem ser feitos.
Atividade em grupo
Com o auxílio de um transferidor, divida a turma em grupos ou individualmente e
peça a eles para descubrirem os ângulos formados . EM ANEXO
AULA 40 – A TRIGONOMETRIA DO TRIANGULO RETÂNGULO
Problematização
Um jovem está a uma distancia de 26 metros de um edifício, sabendo que o ângulo formado
entre o pé dele e o topo do edifício mede 30º . Qual é a altura do edifífio
h
30º
Solução :
Tg 30º =
h
26
3
h
=
26
3
3h= 26.1,73
3h = 44,98
h=
44,98
3
h = 14,99  15 metros
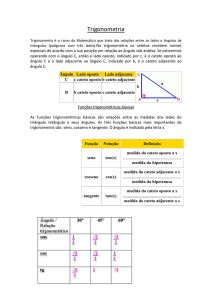
TRIGONOMETRIA NO TRIÂNGULO RETÂNGULO
Em princípio, Trigonometria é o estudo da relações entre as medidas de ângulos e lados nos triângulos retângulos
(trigono = triângulo e metria = medida).
RAZÕES TRIGONOMÉTRICAS
O triângulo é retângulo quando um de seus ângulos internos é reto, ou seja, mede 90°.
Observe-se o triângulo ABC da figura com  = 90° (reto), e seus ângulos agudos
e
.
É importante saber que:
a) Em relação ao ângulo
, temos:
c é o cateto oposto;
b é o cateto adjacente.
b) Em relação ao ângulo
, temos:
b é o cateto oposto;
c é o cateto adjacente.
Seno, cosseno e tangente de um ângulo agudo
Seja
a medida de um ângulo agudo do triângulo acima, temos:
a) Seno do ângulo
(sen
):
É a razão entre a medida do cateto oposto a
b) Cosseno do ângulo
(cos
):
É a razão entre a medida do cateto adjacente
Cos
=
, isto é :
=
a e a medida da hipotenusa, isto é:
b
a
Tangente do angulo
Tg
e a medida da hipotenusa, ou seja:
c
b

( tg
): É a razão entre a medida do cateto oposto a
e a medida do cateto adjacente a
ATIVIDADES :
1) Observando o triângulo retângulo ABC, dê a medida :
a) da hipotenusa ; 5 cm
C
b) do cateto oposto ao  ; 3 cm
c) do cateto adjacente ao Â; 4 cm
3 cm
5 cm
d) do cateto oposto ao C ; 4 cm
e) do cateto adjacente ao C; 3cm
B
2) Exemplo:
senÔ = 3/5 = 0,6
cosÔ = 4/5 = 0,8
tgÔ = 3/4 = 0,75
senÊ = 4/5 = 0,8
cosÊ = 3/5 = 0,6
tgÊ = 4/3 = 1,333....
4 cm
A
3) Uma escada apoiada em uma parede, num ponto distante 4 m dos solo, forma com essa
parede um ângulo de 60°. Qual é o comprimento da escada em metros?
Solução:
4) Calcule o seno, cosseno e tangente dos ângulos
abaixo:
Para obter as razões trigonométricas do ângulo de 45°, considere um quadrado de lado l. A
diagonal divide o quadrado em dois triângulos retângulos isósceles.
No triângulo ABD, temos:
Observação: sen45° = cos45°
ANEXO AULA 39
ATIVIDADE
Calcule os ângulos abaixo .
Exercícios para aa prova
1) Observando o triângulo retângulo ABC, dê a medida :
a) da hipotenusa ;
C
b) do cateto oposto ao  ;
c) do cateto adjacente ao Â;
3 cm
5 cm
d) do cateto oposto ao C ;
e) do cateto adjacente ao C;
B
4 cm
2) Qual é o menor ângulo formado pelos ponteiros do relógio abaixo ?
a) 12º
b) 60º
c) 120º
d)15º
A