CENTRO DE ENSINO SUPERIOR DE CONSELHEIRO LAFAIETE
CURSO DE ENGENHARIA ELÉTRICA
CES-CL
Conversão de Energia
Circuitos Magnéticos
CES- CL Conversão de Energia
Prof. Geraldo Leão Lana
Circuitos Magnéticos
Fluxo Concatenado e Indutância
→ Quando um campo magnético varia no tempo, produz-se um campo elétrico no
espaço de acordo com a lei de Faraday:
d
∫C E ⋅ ds = − dt ∫S B ⋅ da
A equação afirma que a integral de linha da intensidade de campo elétrico E ao
longo de um contorno fechado C é igual à razão, no tempo, da variação de fluxo
magnético que concatena (passa através) aquele contorno. O campo E no fio é
extremamente pequeno podendo ser desprezado, de modo que o primeiro
membro da equação reduz-se ao negativo da tensão induzida e nos terminais do
enrolamento. No segundo membro da equação predomina o fluxo do núcleo,
como o enrolamento concatena o fluxo do núcleo N vezes, a equação reduz-se a:
e=N
dϕ dλ
=
dt
dt
Onde λ é o fluxo concatenado do enrolamento definido como:
λ = Nϕ
Circuitos Magnéticos
Fluxo Concatenado e Indutância
→ Em um circuito magnético, composto de material magnético de permeabilidade
constante ou que inclua um entreferro dominante, a relação entre φ e i será linear
e poderemos definir a indutância L como:
L=
A substituição das equações
λ
i
ℑ
ℑ = Ni = ∫ Hdl; φ =
; λ = Nϕ
ℜtot
na equação anterior nos dá:
N2
L=
ℜtot
Dessa equação, podemos ver que a indutância de um enrolamento em um circuito
magnético é proporcional ao quadrado de espiras e inversamente proporcional à
relutância do circuito magnético associado a esse enrolamento.
Circuitos Magnéticos
Fluxo Concatenado e Indutância
A partir de
µ 0 Ag
ℑ ℑµ 0 Ag
=
= Ni
φ≈
ℜg
lg
lg
supondo que a relutância do núcleo seja desprezível em comparação com a do
entreferro, a indutância do enrolamento será igual a:
L=
(
N2
lg
µ 0 Ag
=
)
N 2 µ 0 Ag
lg
Circuitos Magnéticos
Fluxo Concatenado e Indutância
→ A figura abaixo mostra um circuito magnético com um entreferro e dois
enrolamentos. Neste caso, observe que a FMM do circuito magnético é dada pelo
total de ampéres-espiras que atua no circuito magnético (ambos os enrolamentos) e
que os sentidos de referência das correntes foram escolhidos de modo a produzirem
fluxos no mesmo sentido. A FMM total é
ℑ = N1i1 + N 2i2
Circuitos Magnéticos
Fluxo Concatenado e Indutância
→ Da equação,
µ 0 Ag
ℑ ℑµ 0 Ag
=
= Ni
φ≈
ℜg
lg
lg
desprezando a relutância do núcleo e assumindo que Ac = Ag, o fluxo do núcleo é:
φ = ( N1i1 + N 2i2 )
µ0 AC
lg
Nesta equação φ é o fluxo resultante no núcleo, produzido pela FMM total dos dois
enrolamentos. É esse fluxo resultante que determina o ponto de operação do
material do núcleo. Se esta equação for decomposta em termos relacionados
individualmente com cada corrente, o fluxo concatenado resultante da bobina 1 pode
ser expresso como:
µ 0 AC
λ1 = N1φ = N
lg
2
1
i1 + N1 N 2 µ 0 AC
l
g
Que pode ser escrita como:
λ1 = L11i1 + L12i2
i2
Circuitos Magnéticos
Fluxo Concatenado e Indutância
→ Da equação,
L11 = N
2
1
λ1 = L11i1 + L12i2
µ 0 AC
é a indutância própria da bobina 1 e
L11i1
é o fluxo
lg
concatenado da bobina 1 devido à sua própria corrente i1 .
A indutância mútua entre as bobinas 1 e 2 é:
L12 = N1 N 2
e
L12i2
µ0 AC
lg
é o fluxo concatenado da bobina 1 devido à corrente i2 na outra bobina.
Circuitos Magnéticos
Fluxo Concatenado e Indutância
→ Do mesmo modo, o fluxo concatenado da bobina 2 é
ou
onde
µ 0 AC
λ2 = N 2φ = N1 N 2
lg
λ2 = L21i1 + L22i2
L21 = L12
é a indutância mútua e
L22 = N 22
é a indutância própria da bobina 2.
µ 0 AC
lg
µ 0 AC
2
i1 + N 2
l
g
i2
Exercícios
1) Um núcleo ferromagnético é mostrado abaixo.Três de seus lados têm larguras
uniformes, ao passo que a largura do quarto lado é menor. A profundidade do núcleo
(para dentro da página) é 10 cm e as outras dimensões são mostradas na figura. Uma
bobina de 200 espiras está enrolada no lado esquerdo do núcleo. Assumindo uma
permeabilidade relativa 2500, quanto fluxo será produzido por uma corrente de 1 A?
SOLUÇÃO
Três lados do núcleo têm as mesmas áreas de seção reta, ao passo que o quarto lado
tem uma área diferente. Assim, o núcleo pode ser dividido em duas regiões: (1) um lado
menos espesso e (2) três outros lados tomados em conjunto.
Exercícios
2) O circuito magnético mostrado na figura abaixo tem as dimensões Ac = Ag = 9 cm²,
g = 0,050 cm, lc = 30 cm e N = 500 espiras. Suponha o valor µr = 70.000 para o material
do núcleo. a) Encontre as relutâncias Rc e Rg. Dada a condição de que o circuito
magnético esteja operando com Bc = 1,0 T, encontre (b) o fluxo φ e (c) a corrente i.
SOLUÇÃO
3) Encontre o fluxo φ e a corrente para o Exercício 2 se (a) o número de espiras for
duplicado para N = 1000 espiras, mantendo-se as mesmas dimensões, e (b) se o
número de espiras for N = 500 e o entreferro for reduzido a 0,040 cm.
Exercícios
3) A figura abaixo mostra um núcleo ferromagnético cujo comprimento de caminho
médio é 40 cm. Há um entreferro delgado de 0,05 cm no núcleo, o qual é inteiriço no
restante. A área da seção reta do núcleo é 12 cm2, a permeabilidade relativa do núcleo
é 4000 e a bobina enrolada no núcleo tem 400 espiras. Assuma que o espraiamento no
entreferro aumente a área efetiva da seção reta em 5%. Dada essa informação,
encontre :(a) a relutância total do caminho de fluxo (ferro mais entreferro) ;
(b) a corrente necessária para produzir uma densidade de fluxo de 0,5 T no entreferro.
SOLUÇÃO
Exercícios
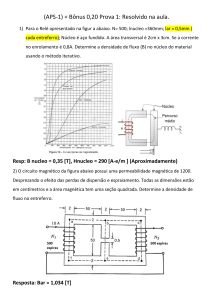
4) A figura abaixo representa o circuito magnético de um relé. A bobina possui 500
espiras e o comprimento médio do núcleo é 360 mm. Quando o comprimento médio de
cada entreferro é 1,5 mm, uma densidade de fluxo de 0,8 T é necessária para a atuação
do relé. O material do núcleo é aço fundido (cast steel).
SOLUÇÃO
a) Calcule a corrente na bobina (utilize a curva B-H fornecida para determinar Hc)
R: 4,19A
b) Calcule os valores da permeabilidade µ e da permeabilidade relativa µr no núcleo
R: µ = 0,00157; µr = 1250
c) Considerando o entreferro igual a zero, calcule a corrente na bobina para a mesma
densidade de fluxo (0,8 T) no núcleo.
R: 0,368A
Exercícios
5) A figura abaixo mostra de forma simplificada o rotor e o estator de um motor CC. O
comprimento do caminho médio do estator é 50 cm e a área de sua seção reta é 12
cm². O comprimento do caminho médio do rotor é 5 cm e pode-se assumir que a área
de sua seção reta é também 12 cm². Cada entreferro entre o rotor e o estator tem 0,05
cm de largura e a área da seção reta de cada entreferro (incluindo o espraiamento) é 14
cm². O ferro do núcleo tem permeabilidade relativa de 2000 e há 200 espiras de fio
sobre o núcleo. Se a corrente no fio for ajustada para 1 A, qual será a densidade de
fluxo resultante nos entreferros?
SOLUÇÃO
Para determinar a densidade de fluxo no entreferro, é necessário calcular primeiro a
força magnetomotriz aplicada ao núcleo e a relutância total do caminho de fluxo. Com
essas informações, pode-se encontrar o fluxo total no núcleo. Finalmente, conhecendo
a área da seção reta dos entreferros, pode-se calcular a densidade de fluxo.
O respectivo circuito magnético dessa máquina está mostrado na figura b. A relutância
total do caminho de fluxo é, portanto,
SOLUÇÃO
Exercícios
6) Uma máquina síncrona de 2 pólos é mostrada abaixo e possui as seguintes
dimensões:
Comprimento de cada entreferro: lg = 2,5 mm
Área da seção transversal dos pólos, Ag = 500 cm²
N = 500 espiras
I=5A
µ=∞
a) Desenhe o circuito magnético equivalente
b) Encontre a densidade de fluxo no entreferro