Departamento de Engenharia Elétrica Conversão de Energia I Lista 1

Departamento de Engenharia Elétrica
Conversão de Energia I
Lista 1
Ex.1) Um circuito magnético como mostrado na figura abaixo, tem dimensões
AC = 9 [cm2]; Ag = 9 [cm2]; lg = 0,050 [cm]; lC = 30 [cm]; N = 500 espiras. Supor o
valor µr = 5.000.µ0 para o ferro. Desprezando os efeitos dos campos de fluxo
disperso e o espraiamento no entreferro. Calcular:
a) A corrente “i” para B = 1 [Wb/m2]; (Resp. I = 0,89 [A])
b) O fluxo concatenado λ = N.Φ. (Resp. λ =0,45 [Wb])
Ex. 2) Um circuito magnético com um único entreferro está mostrado na figura
abaixo. As dimensões do núcleo são:
Área da seção reta Ac = 1,8x10-3 [m2] (lados 1x10-2 [m] por 1,8x10-1[m]);
Comprimento médio do núcleo lc = 0,6 [m];
Comprimento do entreferro g = 2,3x10-3 [m];
N = 83 espiras.
Supondo que o núcleo tenha permeabilidade de µ=2500µ0, e desprezar o
espraiamento no entreferro.
a) Calcule a relutância do núcleo Rc e a do entreferro Rg;
5
5
(Resp. Rc = 1,06.10 [A/Wb]; Rg = 8,17.10 [A/Wb])
b) Para uma corrente de i = 1,5A,Calcule o fluxo total; (Resp. Φ =1,35.10-4 [Wb])
c) Fluxo concatenado da bobina; (Resp. λ =1,12.10-2 [Wb])
d) Indutância L da bobina. (Resp. L =7,47 [mH])
Ex. 3) O circuito magnético da figura abaixo consiste em anéis de material
magnético dispostos em uma pilha de altura h. Os anéis têm raios interno Ri e
externo Re. Suponha que o ferro tenha permeabilidade infinita, e despreze os efeitos
de dispersão e de espraiamento magnéticos. Para:
Ri = 3,4 [cm]; Re = 4,0 [cm]; h = 2 [cm]; g = 0,2 [cm]
a) Calcule o comprimento médio do núcleo lc e a área da seção reta Ac;
2
(Resp. lC = 23,05 [cm]; AC = 1,2 [cm ])
b) a relutância do núcleo Rc e a do entreferro Rg; (Resp. Rc = 0; Rg = 1,33.107 [A/Wb])
Para N = 65 espiras, calcule:
c) a Indutância L; (Resp. L = 0,319 [mH])
d) A corrente “i” requerida para que se opere com uma densidade de fluxo no
entreferro de Bg = 1,35 [T]; (Resp. I = 33,15 [A])
e) o fluxo concatenado correspondente λ da bobina. (Resp. λ =10,5 [mWb])
Ex. 4) O indutor da figura abaixo tem um núcleo de seção reta circular uniforme de
área Ac, comprimento médio lc, permeabilidade relativa µr, e um enrolamento de N
espiras. Escreva uma expressão para a indutância L. (Resp. L =
N 2 ⋅ µ 0 ⋅ AC
)
g + lc µ r
Ex. 5) O indutor do Ex. 4 tem as seguintes dimensões:
Ac = 1,0 cm2; lc = 15 cm; g = 0,8 mm; N = 480 espiras.
Desprezando os campos de espraiamento e de dispersão e supodo µr = 1.000,
calcule a indutância. (Resp. L =30,5 [mH])
Ex. 6) O indutor do Ex. 5 deve operar com uma fonte de tensão de 60 Hz.
a) Supondo uma resistência da bobina desprezível, calcule a tensão eficaz no
indutor que corresponde a uma densidade de fluxo de pico no núcleo de 1,5 [T];
(Resp. V =19,18 [V]
b) Sob essas condições de operação, calcule a corrente eficaz e a energia
armazenada de pico. (Resp. I =1,67 [A], Wpico= 8.50 [mJ])
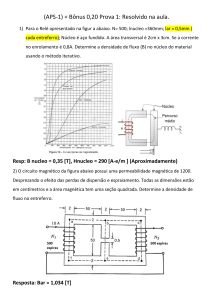
Ex. 7) O desenho apresentado abaixo representa um esquema primitivo de um relé.
A bobina tem 500 espiras e o caminho médio no material magnético é 360 [mm]
(não considerar o entreferro de ar). Quando o entreferro de ar apresenta um
comprimento de 1,5 [mm] cada, uma densidade de fluxo de 0,8 [T] é necessária
para atuar o relé. O núcleo é constituído aço fundido (cast steel). Desprezar o efeito
espraiamento no entreferro.
a) Determine a corrente no enrolamento; (I = 4,19 [A])
b) Calcule o valor da permeabilidade e da permeabilidade relativa do núcleo. (µ =
1,57.10-3 ; µr = 1250 )
c) Se o comprimento do entreferro for zero, qual será a corrente no enrolamento
para a mesma densidade de fluxo (0,8 [T]) no núcleo. ( I = 0,368 [A] )
Obs. A curva BxH do aço fundido e apresentada no Anexo I.
Ex. 8) No circuito magnético apresentado abaixo, a permeabilidade relativa do
material ferromagnético é 1200. Desprezar o fluxo de dispersão e o efeito
espraiamento no entreferro. Todas as dimensões estão em centímetros e o material
magnético tem uma secção quadrada de área. Determine o fluxo no entreferro, a
densidade de fluxo e a intensidade do campo no entreferro. ( Φg = 4,134.10-4 [Wb];
Bg = 1,034 [T]; Hg = 0,822.106 [A/m] )
Ex. 9) A bobina da figura abaixo tem 250 espiras e o núcleo é de chapas de aço
silício (silicon sheet steel). O raio interior e exterior são 20 e 25 [cm]
respectivamente, e o núcleo do toroide tem secção circular. Para uma corrente de
2,5 [A] na bobina, determine:
a) A densidade de fluxo magnético no raio médio do toroide; ( B = 1,225 [T] )
b) A indutância da bobina, assumindo que a densidade de fluxo dentro do núcleo é
uniforme e igual a obtida no raio médio do teroide. ( L = 240,4 [mH] )
Obs. A curva BxH do aço silício e apresentada no Anexo I.
Ex. 10) O circuito magnético apresentado na Fig. 1 e feito com um núcleo de
material ferromagnético, cuja a curva BxH do material é mostradas na Fig. 2, essa
curva foi aproximado para retas. As bobinas N1 = 200 espiras e N2 = 100 espiras.
a) Se I1 = 2 [A], calcule o valor de I2 necessário para produzir uma densidade de
fluxo de 0,6 [T] no circuito magnético (Comente se a corrente está conforme
apresentada na Fig. 1 ou em sentido contrário); ( I2 = -3,1 [A] )
b) Se I1 = 0 [A], qual deve ser o valor mínimo da corrente I2 para levar o núcleo a
saturação. ( I2 = 3,0 [A] )
Obs. Negligenciar a dispersão magnética.
Ex. 12) Suponha que o circuito magnético do Ex. 1 seja construído de aço elétrico
M-5 com propriedades descritas nas figuras apresentadas na Aula. Suponha que o
núcleo esteja operando com uma densidade de fluxo senoidal de 60 Hz e valor
eficaz de 1,1 T. Desconsidere a resistência do enrolamento e a indutância de
dispersão. Obtenha a tensão do enrolamento, a sua corrente eficaz e as perdas no
núcleo, nessas condições de operação. A densidade do aço M-5 é 7,65 g/cm³.
(Vef = 46,7 V, Pc=10,4 W, Ief 29.4 A).
Ex.13) Um Circuito magnético de núcleo toroidal tem raio externo re= 12 cm e raio
interno re= 8 cm e seção reta bruta igual a 16,2 cm². A característica B-H, a de
potência aparente ( Volt-ampère eficazes) e as perdas do material de aço elétrico
M-5 que é usado no núcleo foram apresentadas em aula. O aço ocupa 0,97(fator
de empilhamento) da área da seção reta. Se a fonte de tensão que alimenta a
bobina for ajustada para V(t)= 220
sen(2π60t) e a resistência da bobina de 400
espiras for insignificante, determinar:
a) o volume e a massa do núcleo
b) a femm gerada na bobina pelo fluxo no núcleo;
c) a densidade de fluxo magnético
d) a intensidade de campo magnético aplicado
e) a corrente de excitação em valor eficaz
f) a resistência elétrica que representa ás perdas no núcleo ( ou no ferro)
g) a componente da corrente de excitação associada às perdas no núcleo .
h) a componente da corrente de excitação associada à magnetização.
i) a indutância de magnetização do dispositivo.
ANEXO: A curva B-H de vários materiais ferromagnéticos