ÂNGULOS.

ÂNGULOS
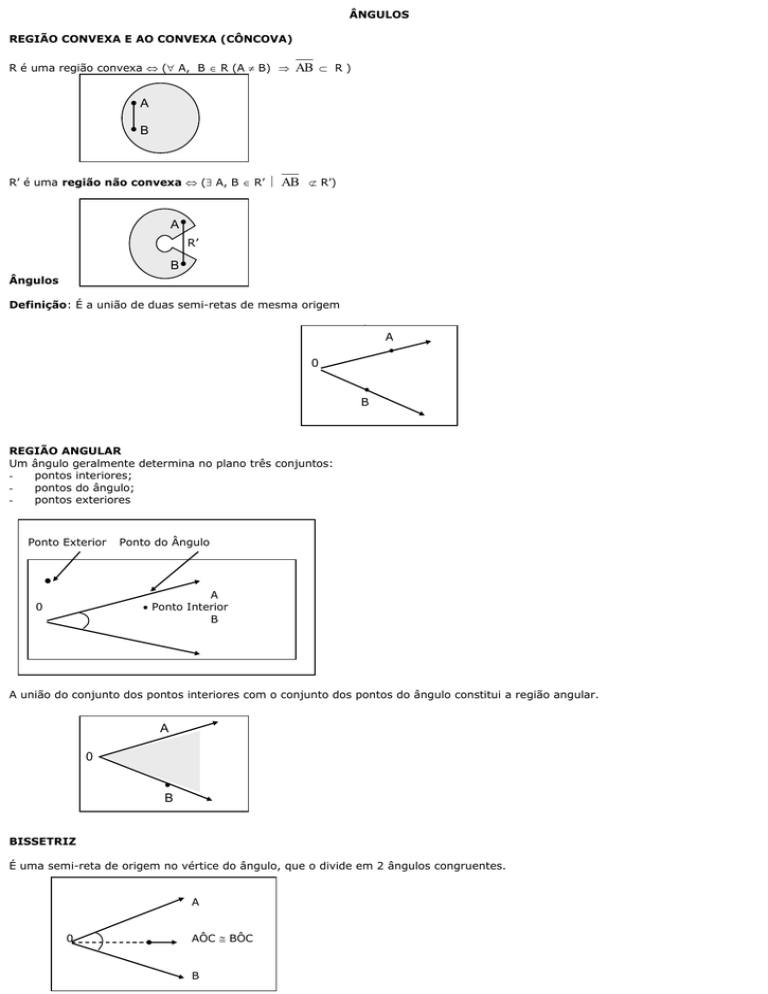
REGIÃO CONVEXA E AO CONVEXA (CÔNCOVA)
R é uma região convexa  ( A, B  R (A  B) 
AB  R )
A
R
B
R’ é uma região não convexa  ( A, B  R’ 
AB  R’)
A
R’
B
Ângulos
Definição: É a união de duas semi-retas de mesma origem
1)
A

0

B
REGIÃO ANGULAR
Um ângulo geralmente determina no plano três conjuntos:
pontos interiores;
pontos do ângulo;
pontos exteriores
Ponto Exterior
Ponto do Ângulo

A
 Ponto Interior
B
0
A união do conjunto dos pontos interiores com o conjunto dos pontos do ângulo constitui a região angular.
A

0

B
BISSETRIZ
É uma semi-reta de origem no vértice do ângulo, que o divide em 2 ângulos congruentes.
A
0
AÔC  BÔC
B
ÂNGULOS CONSECUTIVOS E ADJACENTES
São consecutivos dois ângulos que possuem um lado em comum:
Exemplo:



Os ângulos 1 e 2 , 1 e



3 , e 2 e 3 , da figura são consecutivos.


2
3

1
São adjacentes dois ângulos consecutivos cujas regiões angulares se interceptam no lado comum. Na figura anterior são adjacentes


somente os ângulos 1 e 2 .
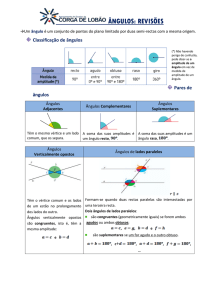
ÂNGULOS OPOSTOS PELO VÉRTICE
São ângulos cujos lados de um são semi-retas opostas aos lados do outro.
a
b
ÂNGULOS: RETO, AGUDO E OBTUSO
reto
agudo
obtuso
ÂNGULOS COMPLEMENTARES, SUPLEMENTARES E REPLEMENTARES

Complementares:
Se aˆ  bˆ  90 º

a
Suplementares:
Se aˆ  bˆ  180 º
b

Replementares:
Se aˆ  bˆ  360 º
EXERCÍCIOS PROPOSTOS
01. O dobro do complemento de um ângulo é igual à quinta parte do suplemento desse ângulo. A medida do ângulo é igual a:
a) 80º
b) 60º
c) 40º
d) 30º
e) 20º
02. O triplo do complemento de ângulo é igual à terça parte do suplemento deste ângulo. Este ângulo mede:
a) 45º
b) 48º30’
c) 56º15’
d) 60º
e) 78º45’
03. Com os dados da figura seguinte, onde r//s, identifique:
a) os pares de ângulos correspondentes (congruentes):
1e
2e
3e
4e
b) os pares de ângulos alternos internos (congruentes):
3e
4e
1e
2e
3e
4e
c) os pares de ângulos alternos (congruentes):
d) os pares de ângulos internos (suplementares):
e) os pares de ângulos colaterais externos (suplementares)
1e
2e
04. Sabendo-se que r//s e t é uma transversal a r e a s, conforme a figura seguinte, é correto afirmar:
a)
b)
c)
d)
e)
x mede 80º, y e z são correspondentes
y mede 100º, x e z são suplementares
z mede 80º, x e y são opostos pelo vértice
y mede 80º, x e z são alternos externos
z mede 100º, y e x são alternos internos.
RETAS PARALELAS
Nomenclatura
Dadas, num plano, duas retas r e s e uma transversal t, obtém-se oito ângulos com as seguintes denominações:

Alternos internos

Alternos externos
cˆ e xˆ;
dˆ eyˆ

aˆ e zˆ; bˆ e wˆ
Colaterais internos cˆ e yˆ ; dˆ e xˆ

Colaterais externos {a e w, b e z}.
Observação:
Se as retas r e s fossem paralelas e a transversal t não fosse perpendicular à r e s, então os oito ângulos determinados seriam tais
que: quatro deles seriam agudos e congruentes, os outros quatro seriam obtusos e congruentes e finalmente cada ângulo obtuso e
cada ângulo agudo, seria um o suplemento do outro, conforme a figura seguinte:
PARALELISMO
Ângulos de lados paralelos possuem nomes e propriedades especiais.

Ângulos correspondentes

Ângulos alternos

Ângulos colaterais

Ângulos de lados paralelos são CONGRUENTES ou SUPLEMENTARES.
PERPENDICULARISMO
Ângulos de lados perpendiculares são CONGRUENTES ou SUPLEMENTARES.
EXERCÍCIOS PROPOSTOS
01.As retas r e s são interceptadas pela transversal “t”, conforme a figura. O valor de x para que r e s sejam paralelas é:
a) 20º
b) 26º
c) 28º
d) 30º
e) 35º
02.Na figura, as retas r e s são paralelas, o ângulo 1 mede 45º e o ângulo 2 mede 55º. A medida, em graus, do ângulo 3 é:
a) 50º
b) 55º
c) 60º
d) 80º
e) 100º
d) 50º
e) 60º
03. Valor de  na figura seguinte é:
a) 20º
b) 30º
c) 40º
04.Demonstre que a soma das medidas dos ângulos internos de um triângulo qualquer é igual a 180º.
05.Para calcular a circunferência terrestre, o sábio Eratóstenes valeu-se da distância conhecida de 800 km entre as localidades de
Alexandria e Siena no Egito (A e S, respectivamente), situadas no mesmo meridiano terrestre. Ele sabia que, quando em Siena
os raios solares caíam vertical-mente, em Alexandria eles faziam um ângulo de 7,2º com a vertical. Calcule, com esses dados, a
circunferência terrestre, isto é, o comprimento de uma volta completa em torno da Terra.
TRIÂNGULOS
Definição
____
____
____
Dados três pontos não alinhados A, B, e C, chama-se triângulo a união dos segmentos AB , BC e C A
A
C
B
 ABC =
____
REGIÃO ANGULAR
É a união do triângulo ABC com o conjunto dos pontos interiores.
A
B
Elementos do triângulo:
C
____
____
AB  BC  CA

Vértices: A, B, C


Lados AB , BC , AC
Ângulos internos:
____
____
____
  BÂC, B̂  AB̂C e Ĉ  AĈB

Ângulo externo: é o ângulo formado por um lado e a reta suporte do outro, suplementar ao ângulo interno. Na figura, por
exemplo, é o ângulo .
PROPRIEDADES IMPORTANTES

Lei angular de Tales
A soma dos ângulos internos de qualquer triângulo é 180º, pois como   Ĉ e   B̂ (alternos internos) e  = Â , resulta:

Teorema do ângulo externo: em qualquer triângulo, cada ângulo externo é igual à soma dos internos não adjacentes.
Êx  Ĉ  180º
  B̂  Ĉ  180º

Assim: Êx  Ĉ  Â  B̂  Ĉ  Êx  Â  B

Soma dos ângulos externos: em qualquer triângulo, a soma dos ângulos externos é 360º.

 +  +  = 360º
2)
Desigualdade nos triângulos: em todo triângulo, ao maior lado se opõe o maior ângulo e vice-versa.
CLASSIFICAÇÃO DOS TRIÂNGULOS

Quanto aos lados:
eqüilátero
isósceles
escaleno
-
Eqüilátero: os três lados são congruentes.
Isósceles: dois lados são congruentes.
Escaleno: os três lados são não congruentes.

Quanto aos ângulos:
C
A 
B
Retângulo ( Â = 90º)
A
B
Acutângulo (
Aˆ , Bˆ , Cˆ < 90º)
C
A
B
-
C
Obtusângulo
Retângulo: possui um ângulo reto.
Acutângulo: possui os três ângulos agudos.
Obtusângulo: possui um ângulo obtuso.
EXERCÍCIOS PROPOSTOS
01. No triângulo ABC da figura seguinte,  é a medida do ângulo externo do vértice A. Os ângulos internos de vértices A, B, e C
medem, respectivamente, x, y e z. Prove que  = y + z
Na figura seguinte, o valor de  é:
a) 90º
b) 95º
c) 100º
d) 110º
e) 120º
02.Na figura abaixo, a = 100º e b = 110º. Quanto mede o ângulo x?
a) 30o
b) 50o
c) 80o
d) 100o
e) 150o
03.No retângulo abaixo, o valor em graus, de  +  é:
a) 50º
b) 90º
c) 120º
d) 130º
e) 220º
04.As retas t e s são paralelas. A medida do ângulo x, em graus , é
a) 30º
b) 40º
c) 50º
d) 60º
e) 70º