exp_magnetizador

Roteiro Experimental n° da disciplina de Materiais Elétricos
Roteiro desenvolvido por: Camila Scalabrini e Ruam Pessoa
“ MAGNETIZADOR”
COMPONENTES DA EQUIPE:

NOTA:


Data: ___/___/___

1. OBJETIVOS:

Mostrar como os domínios magnéticos de comportam em diferentes
materiais;

Porque em materiais moles a magnetização é menor que em materiais
duros;

Como os imãs são magnetizados

Qual a relação dos campos vetoriais B (indução magnética), H (campo
magnético) e M(campo de magnetização) na magnetização dos
materiais;

Comprovar física e matematicamente a dispersão do fluxo magnético;

Fazer a analise da conversão de energia, de uma energia elétrica para
uma magnética.

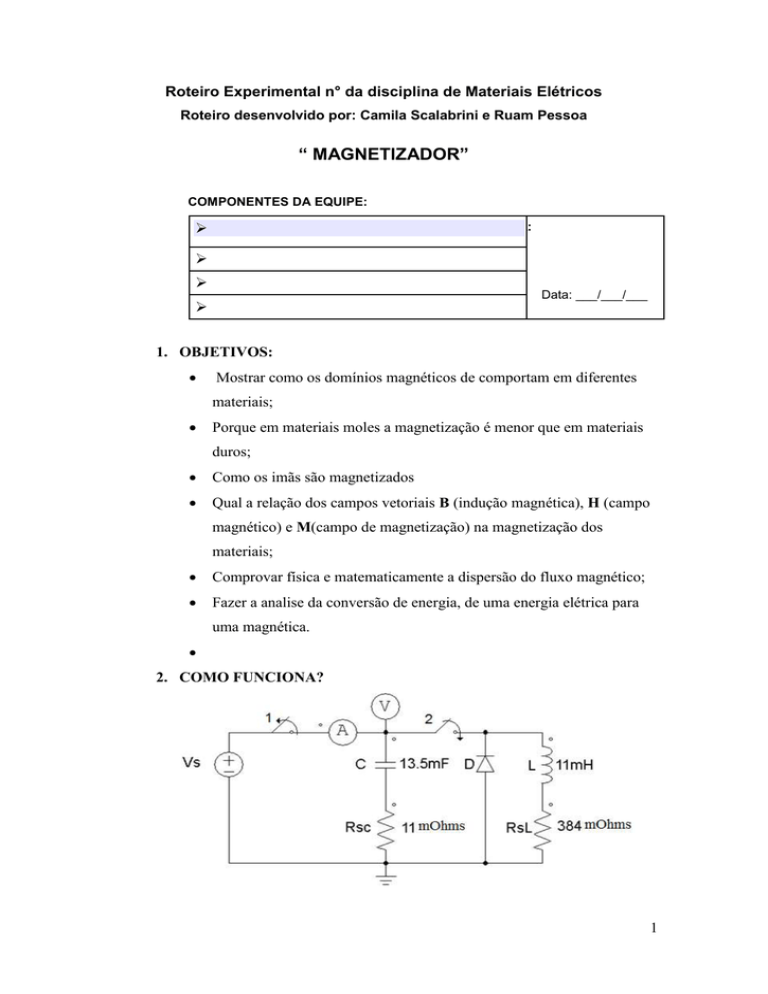
2. COMO FUNCIONA?
1
Figura 1: Circuito elétrico completo do magnetizador
O circuito elétrico do magnetizador esta apresentado na figura 1. Ele funciona da
seguinte forma, carregasse um banco de capacitores lentamente para que não haja danos
ao circuito, com a chave 1 fechada e a chave 2 aberta, quando os capacitores estiverem
carregados, abre-se a chave 1 e fecha-se a chave 2. Nesse instante acontece uma
transferência de energia, a energia armazenada no capacitor vai se transferir para o
indutor, como um pico de corrente, isso gera um campo magnético 𝑯, com um fluxo 𝜑,
uma densidade de fluxo 𝑩. Esse fluxo irá passar pelo ferrite e como o ferrite é um
material magnético-duro irá armazenar parte da energia do capacitor.
3. Análise do circuito
Como temos elementos reais e não ideais, teremos perdas na forma de calor,
principalmente nas resistências série do indutor e do capacitor, essa energia deverá ser
descontada na formula da conversão de energia, Vale lembrar que ainda uma parte da
energia se converterá em dispersão calcular essa energia é um dos objetivos deste
trabalho.
Figura 2: Mostra o comportamento do circuito sem o diodo e com o diodo,
mostrando sua necessidade.
O diodo em roda-livre completa o circuito não deixando que uma corrente de pico
reversa desmagnetize a ferrite, isso poís quando fechar a chave o circuito se comportará
como um circuito de segunda ordem sobreamortecido(figura 2), como veremos no
equacionamento.
2
4. Equacionamento
Para saber qual é a corrente de pico e como ela se comporta iremos equacionar a
carga e descarga no indutor:
Figura 3: Circuito de carga do indutor, já transformado em Laplace
Começando pela carga, circuito da figura 3.
Analise para 𝑡 < 0;
𝑣𝑐 (0) = 𝑉𝑠 ; 𝑖𝑐 (0) = 0.
transformado o circuito em Laplace e aplicando a lei das malhas de kirchoff:
−
𝑣(0)
𝐼
+ 𝑅𝑆𝐶 𝐼(𝑆) +
+ 𝑅𝑠𝐿 𝐼(𝑆) + 𝑆𝐿𝐼(𝑆) = 0
𝑆
𝑆𝐶
Equacionando:
−
𝑣(0)𝐶
𝐿𝐶𝑆 2 + (𝑅𝑠𝐶 + 𝑅𝑠𝐿 )𝐶𝑆 + 1
= 𝐼(𝑆) (
)
𝑆𝐶
𝑆𝐶
𝐼(𝑆) =
𝐶𝑣(0)
(𝑅 + 𝑅 )
1
𝐿𝐶(𝑆 2 + 𝑠𝐶 𝐿 𝑠𝐿 𝑆 + 𝐿𝐶 )
Onde:
𝐶 = 13,5𝑚𝐹, corresponde à soma em paralelo de 9 capacitores de 1500uF
𝐿 = 11𝑚𝐻, corresponde a indutância do indutor medida experimentalmente
𝑅𝑆𝐶 = 11𝑚𝛺, corresponde à o paralelo da resistências serie dos 9 capacitores(data
sheet)
𝑅𝑠𝐿 = 384𝑚𝛺 ,medida experimentalmente
𝑣(0) = 𝑉𝑠 , tensão armazenada no capacitor (regulada com o varivolt)
Substituindo os valores
3
𝐼(𝑆) =
13,5𝑚 𝑣(0)
148,5𝜇(𝑆 2 + 35,91𝑆 + 6,73𝐾)
𝑖(𝑡) = 𝐿−1 {𝐼(𝑆)}
𝑖(𝑡) =
90,9𝑣(0) −𝑡(0,09875−𝑗82) 90,9𝑣(0) −𝑡(0,09875+𝑗82)
𝑒
+
𝑒
0,1317
0,1317
Para sabermos o tempo de pico, derivamos a equação e igualamos a 0
𝜋
𝑡𝑝 = 82 = 0,038𝑠 ; observamos que o tempo de pico não depende da tensão aplicada no
capacitor.
Substituído o tempo de pico na equação da corrente no tempo obtemos a corrente de
pico.
𝑖(𝑡 = 0,038) = 𝑣(0)𝑒 −0,09875 ∙0,038 cos(𝑗82 ∙ 0,038)
Assim, como sabemos que 𝑁 = 130 𝑒 𝑙𝑚 = 18𝑐𝑚:
𝐻=
𝑁𝑖
𝑙𝑚
Substituindo a corrente de pico, sabemos o H.
Figura 4: Circuito de descarga do indutor
Descarga do indutor figura 4.
Para 𝑡 < 𝑡𝑝
𝑣𝐿 = 𝑣𝐶 (0) ; 𝑖 = 𝑖𝑃
Para 𝑡 > 𝑡𝑝 em Laplace:
𝐼(𝑆)𝑅𝑠𝐿 + 𝐼(𝑆)𝐿𝑆 − 𝐿𝑖(0) = 0
4
𝐼(𝑆)(𝑅𝐿 + 𝐿𝑆) = 𝐿𝑖(0)
𝐼(𝑆) =
𝐿𝑖(𝑜)
𝑅
𝐿 (𝑆 + 𝐿𝑠𝐿 )
𝑖(𝑡) = 𝐿−1 {𝐼(𝑆)}
𝑖(𝑡) = 𝑖(0)𝑒 −34,91t
5. Análise da conservação de energia.
𝑊𝑐 = 𝑊𝐻 + 𝑊𝑃
Onde,
𝑊𝑃 = 𝑊𝐷 + 𝑊𝑟𝑒𝑠
Sabendo que a energia de um capacitor é:
1
𝑊𝐶 = 𝑣 2 𝐶
2
Que a energia do campo magnético e dada por
𝑊𝐻 = ∫ 𝐻 𝑑𝐵
E sabendo que podemos calcular H pela lei de amper
∮ 𝐻 ∙ 𝑑𝐿 = 𝑁𝑖
𝑙𝑚
Resolvendo a integral, chegamos em:
𝐻=
𝑁𝑖
𝑙𝑚
Da equação de carga do indutor sabemos quanto vale 𝑖𝑝 , substituindo na
formula, junto com 𝑁 = 130 𝑒𝑠𝑝𝑖𝑟𝑎𝑠 e 𝑙𝑚 = 18𝑐𝑚 Conseguimos calcular qual o valor
máximo do campo magnético.
Sabendo que a energia magnética é a região abaixo da curva BH, tal como na
figura 4. E aproximando essa área a área de um triangulo, para facilitar os cálculos.
Chegamos na seguinte expressão:
1 1
1
𝑊𝐻 ≅ ( 𝐵𝐻) = 𝐵𝐻
2 2
4
5
Figura 4: Curva de magnetização de um imã aproximada
Figura 5: Curva reais de diferentes imãs, mostrando quais são suas características.
6
A indução magnética foi medida experimentalmente com um aparelho chamado
teslômetro, que usa de um sensor hall para medir a indução.
Vs (V)
B+ (mT)
B-(mT)
H (A/m)
50,2
77,8
90,6
100,4
125,4
151,5
176,4
23,2
36,3
22,5
39,5
40,2
26,2
39,1
35,1
25,8
33,4
26,3
26,5
39,8
24,16
166570,6
258151,3
300623,5
333141,3
416094,8
502698,2
585319,9
Tabela 1: Mostra como o campo magnético e a indução magnética se comportam
variando a tensão no capacitor valores de referencia
Tabela 2: Características magnéticas das curvas de diferentes composições para
imãs
E estão apresentadas na tabela 1 conforme a tensão aplicada nos capacitores é
curioso que a indução não tem o mesmo valor do lado positivo e do lado negativo, isso
se deve a dispersão, pois mais linhas ou tubos de fluxo passam pela superfície onde a
indução é negativa do que os da superfície onde a indução é positiva. Outra análise
importante é que a indução não varia muito, isso se deve ao fato de o material já ter
chegado na saturação e então o B remanente não varia muito com muita variação do H.
Com isso conseguimos calcular a energia transmitida diretamente para a ferrite.
1
𝐵𝐻
4
A energia perdida nas resistências, podemos calcular da seguinte forma:
𝑊𝐻 =
𝑑𝑊
= 𝑃 = 𝑅𝑖 2 = (𝑅𝑠𝐶 + 𝑅𝑠𝐿 )𝑖𝑝2
𝑑𝑡
𝑊𝑟𝑒𝑠 = (𝑅𝑠𝐶 + 𝑅𝑠𝐿 )𝑖𝑝2 𝑡
7
Do equacionamento conseguimos 𝑖𝑝 e 𝑡 que é o tempo que a corrente demora para
chegar a 0.
Assim conseguimos que a energia perdida na dispersão é:
𝑊𝐶 = 𝑊𝐻 + 𝑊𝑟𝑒𝑠 + 𝑊𝐷
𝑊𝐷 = 𝑊𝐶 − 𝑊𝐻 − 𝑊𝑟𝑒𝑠
Onde :𝑊𝑐 é a energia armazenada no capacitor, 𝑊𝐻 é a energia armazenada no campo
magnético, 𝑊𝑟𝑒𝑠 é a energia perdida nas resistências e 𝑊𝐷 é a energia dissipada.
2. MATERIAL UTILIZADO
 Magnetizador ;
 Ferrite dura;
 Neodino ferro boro;
3. EXPERIMENTO
Coloque algum material dos sugeridos pelo professor no magnetizador, aplique
uma tensão de 175V (o máximo desses capacitores é 200V, não devemos trabalhar
com essa tensão, se por um acaso o professor não lembrar, avise-o) lentamente
controlando a corrente (cuidado o capacitor pode explodir ou você pode danificar algum
instrumento se carregar o capacitor muito rápido), quando estiver com 175V, abra a
chave 1 (figura1) e feche a chave 2, abaixe a tensão da fonte e repita o experimento com
os outros materiais.
Agora vamos variar a tensão e analisar como a magnetização aumenta, escolha
tensões menores que 200V, não escolha 200V e faça o procedimento anterior.
Questões:
a) Qual é o material que apresentou magnetismo maior? Explique por quê.
b) Existe ferrite mole e dura, explique quais são as diferenças delas, quanto a curva
de histerese, quanto a aplicação, quanto a composição e as propriedades
eletromagnéticas.
8
c) Explique por que o diodo em roda-livre é importante no circuito, qual o
comportamento do gráfico da figura 2 antes do ponto e depois do ponto tanto
para a corrente com o diodo como para a corrente sem o diodo.
d) O que é B remanescente e H coercitivo?
e) Estime, matematicamente qual será a corrente de pico do circuito com uma
tensão de 200V, por que ela não pode ser medida com um multímetro ou com
uma sonda de corrente em um osciloscópio?
f) O que você conclui com a analise de perdas?
g) Aonde se concentra a maior energia no indutor, e por quê?
9