resolução fau2

RESOLUÇÃO – 2º Simulado FAU
ETAPA
01.
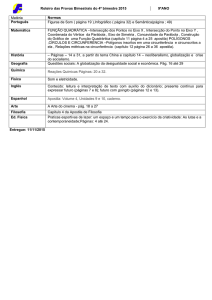
Descrição:
1. Determinar V e X, intersecção da reta PQ com FB e AB, respectivamente.
2. Determinar S e Y, intersecção da reta PR com DH e AD, respectivamente.
3. Determinar U e T, intersecção da reta XY com BC e CD, respectivamente.
4. O Hexágono QRSTUV é a intersecção do plano PQR com o cubo ABCDEFGH.
Justificativa:
Considere as seguintes semelhanças:
∆VFQ ~ ∆VBX ~ ∆PEQ , ∆SHR ~ ∆SDY ~ ∆PER , ∆XAY ~ ∆XBU ~ ∆TDY
Como consequência temos:
3 FV
=
⇔ FV = 6 ⇒ BV = 6 ⇒ V = (12,0,6 )
4
8
3
6
⇔ =
⇔ BX = 8
4 BX
3 HS
⇔ =
⇔ HS = 6 ⇒ DS = 6 ⇒ S = (0,12,6 )
4
8
3
6
⇔ =
⇔ DY = 8
4 DY
Como o triângulo AXY é isósceles, (AX = AY = 20), BU = BX = 8 ⇒ U = (12,8,0 ) e DT = DY = 8 ⇒ T = (8,12,0)
PE
EQ
PE
EQ
PE
ER
PE
ER
FV
FQ
BV
=
BX
HS
=
HR
DS
=
DY
=
⇔
02. a) Construção:
Descrição:
1. Desenhe o quadrado de lado AB eetermine o
ponto médio M, do segmento dado
2. Trace as diagonais do quadrado e a
circunferência de centro O (encontro das
diagonais) e raio AB/2
3. Sendo C o ponto em que a circunferência
intercepta a diagonal AB´, trace uma reta
passando por C e perpendicular a A´B´, cruzando
este último em D.
4. Determine T, encontro da bissetriz do ângulo
B´CD e de A´B´.
5. Trace uma paralela a CD passando por T e
determinando o centro O2 da circunferência
média sobre AB´.
6. Trace a circunferência de centro O2 e raio O2C,
tangente a A´B´ em T e à primeira circunferência
em C.
Justificativa:
Como a circunferência média deve ser tangente
ao quadrado, seu centro deve equidistar dos
lados deste e portanto, deve pertencer a
diagonal AB´. Sabendo ainda que as duas
circunferências são tangentes, seus centros e o
ponto de tangência C devem estar alinhados e
O2C = O2T, em que T é o ponto de tangência da
circunferência média com um dos lados do
quadrado. Logo, o triângulo CTO2 deve ser
isósceles com ângulo da base igual a:
B´O2T 45 º
, que justifica a construção da
=
2
2
bissetriz do ângulo TCD.
b) Construção:
Descrição
1. Trace dois arcos com centros em A e B e raio AB
detreminando C, encontro enetre eles
2. Determine M, ponto médio de AB
3. Com centros em A e M trace dois arcos de raio AM,
detreminando D, ponto de intercecção entre eles.
4. Repita o procedimento 3 para arcos com centro em B e M,
detreminando E.
5. Encontre N, ponto médio de AM
6. Com centros em A e B e raio BN, detremine O, centro da
circunferência tangente aos arcos.
7. Trace as semi-retas AO e BO detreminando T, U, V e W
sobre os arcos traçados em 1, 3 e 4. Trace a circunferência de
centro O e raio OT
Justificativa.
Como os triângulos curvilíneos menores possuem lados
tangentes e centros colineares, os raios para traçarmos seus
arcos são AB/2.
A circunferência traçada em 7 deve ser tangente a todos os
arcos da figura, ou seja, B, T, O e U devem estar alinhados,
assim como A, V, O e W. Desta forma, seu diâmetro mede BU
– BT = AB – BM = BM, ou seja, BO = AO = BM + MN = BN.
03. a)
Construção
1) Num sistema de eixos coordenados de origem A seja AB = 1, B=(1,0). Trace uma semi-circunferência de centro na origem
e raio 4 (no semi plano abaixo do eixo x)
2) Trace um arco com centro em (2,0) e raio 2 e determine C neste arco tal que AC = 2.
3) Trace uma paralela ao eixo x passando por C determinando D, intersecção desta reta com o primeiro arco.
4) Com centro em A e raio BD, determine E e F sobre o eixo x.
5) As paralelas ao eixo y que passam por E e F determinam na semi-circeunferência os pontos P e Q de intersecção das
funções f e g.
6) O gráfico de g pode ser obtido espelhando-se os pontos da parábola y = 4 − x 2 em relação ao eixo x. Note que essa
parábola tem raízes nos pontos (2,0 ) e (− 2,0 ) e vértice em (0,4 )
Justificativa:
O(s) ponto(s) de intersecção dos gráficos de f e g são soluções do sistema
y = − 16 − x
y = −4− x
2
− 4 − x = − 16 − x
2
2
⇔
y = −4− x
t = 0 ou t = 7
⇔ t = x2
(−
2
2
x 2 = 0 ou x 2 = 7
⇔ t = x2
y = − 4 − x2
)
⇔
y = − 4 − x2
4 − x = 16 − x
2
⇔
y = −4− x
2
x = 0 ou x = ± 7
y = −4− x
2
2
(4 − t )2 = 16 − t
⇔ t = x2
y = − 4 − x2
t 2 − 7t = 0
⇔ t = x2
y = − 4 − x2
Ou seja, os pontos de intersecção são (0,−4 ) ,
(
)
7,−3 e
7 ,−3 .
y 2 = 16 − x 2
y 2 + x 2 = 42
, ou seja, o gráfico de f é uma semi-circunferência de raio 4 cujos pontos
y = − 16 − x ⇔
⇔
y ≤0
y ≤0
2
tem ordenada negativa. Como BC é a altura de um triângulo equilátero de vértices A, C e(2,0), BC é perpendicular ao eixo x e
mede
3 . Aplicando o teorema de Pitágoras, BD = 7 , que nos permite encontrar com precisão os pontos de intersecção.
03. b) Construção
h
Descrição e Justificativa
Para determinarmos o gráfico de h : R + → [− 4,+∞[ , definida por h(x ) = x 2 − 4 , utilizamos os pontos C (0,−4 ) , D(1−
, 3) ,
E = (2,0) e F = (3,5 ) . Observe que o vértice a parábola definida por h é C (0,−4 ) , ou seja, como h : R + → [− 4,+∞[ ,
trata-se apenas de “metade” de uma parábola.
Para determinar o gráfico de i (x ) = 3 − h(x + 2) , basta seguir o seguinte roteiro:
a)
b)
c)
d)
04.
Desloque h duas unidades para a esquerda,
Encontre o simétrico do gráfico obtido em a, em relação ao eixo x.
Desloque o gráfico obtido em b três unidades para cima
Desenhe os simétricos dos pontos do gráfico obtido em c que tem ordenada negativa em relação ao eixo x e descarte os
originais.