LISTA 01 DE EXERCÍCIOS – GEOMETRIA PLANA – PROF

11. Um navio dispõe de reservas suficientes para alimentar 14 homens durante 45 dias,
mas recebe 4 sobreviventes de um naufrágio. As reservas de alimento darão para no
máximo quantos dias?
LISTA 01 DE EXERCÍCIOS – GEOMETRIA PLANA – PROF. ROGERINHO
12. Se 16 operários levam três dias para completarem uma certa obra, quantos operários
seriam necessários para completarem essa mesma obra em dois dias?
1º Ensino Médio
(Razão e proporção, potências e radicais, ângulos, paralelismo, ângulos no
 , congruência e polígonos)
13. (UNESP-2011) Os professores de matemática e educação física de uma escola
organizaram um campeonato de damas entre os alunos. Pelas regras do campeonato,
cada colocação admitia apenas um ocupante. Para premiar os três primeiros
colocados, a direção da escola comprou 310 chocolates, que foram divididos entre os
1º, 2º e 3º colocados no campeonato, em quantidades inversamente proporcionais aos
números 2, 3 e 5, respectivamente. As quantidades de chocolates recebidas pelos
alunos premiados, em ordem crescente no campeonato, foram:
a) 155, 93 e 62.
d) 150, 103 e 57.
b) 155, 95 e 60.
e) 150, 105 e 55.
c) 150, 100 e 60.
Nome:__________________________________________ n° _______ turma _________
01. A razão de dois números é 2/3. Ache esses números sabendo que a soma deles é 15.
02. As idades de duas pessoas estão na razão de 6 para 7. Calcule essas idades sabendo
que elas diferem de 8 anos.
03. A largura e o comprimento de um retângulo estão na razão de 3 para 7. Admitindo-se
que o perímetro desse retângulo seja 60cm, calcule as dimensões desse retângulo.
14. Calcule o valor de cada expressão
04. Dividir 360 em partes diretamente proporcionais aos números 2, 5 e 11.
3
05. A soma das medidas dos lados de um triângulo é 24cm. Ache os lados desse
triângulo sabendo que suas medidas são proporcionais a 3, 4 e 5.
06. Michel, Flávio e Anderson formaram uma sociedade. O primeiro entrou com R$
6000,00, o segundo com R$ 8000,00 e o terceiro com R$ 4000,00. Ao fim de seis
meses houve um lucro de R$ 3600,00, que foi dividido entre os três. Quanto coube a
cada um?
2
a)
1 1
(USF - adaptada)       2 3  16 0
2 4
b)
16 0, 25  8

1
3
1
42
15. (FSA) A metade de 4 10 é:
a) 2 19
b) 2 10
07. Os números da sucessão 2, x, y são inversamente proporcionais aos da sucessão 15,
6, 5. Calcule x e y.
c) 2 5
d) 4 5
e) 4 8
16. (FUVEST) Qual desses números abaixo é igual a 0,0064 ?
 1 
a)  
 80 
08. Dividir 45 em partes inversamente proporcionais aos números 3, 4 e 6.
2
1
b)  
8
2
2
c)  
5
3
 1 
d) 

 800 
2
09. Abrindo completamente 4 torneiras idênticas consegue-se encher um tanque com
água em 72 minutos. Se utilizarmos 6 dessas torneiras em quanto tempo encheremos
o tanque?
17. (PUC-SP)Se a  16 e x  1,25 , quanto vale a x ?
10. Um trem, rodando a uma velocidade constante de 50 km/h vai de São Paulo ao Rio
em 8 horas. Em quanto tempo fará a mesma viagem se a velocidade passar para 80
km/h?
19. (GV) Se x  3200000 e y  0,00002 , calcule o valor do produto x. y .
18. Calcule o número de algarismos do produto 517  4 9 .
20. (MACK) Calcule o valor de 2 x 0  x
1

3
4
 18x  0,5 para x  81 .
8
e)  
 10 
3
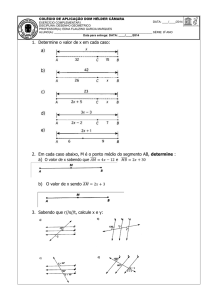
31. Determine o valor de  em cada caso:
a)
b)
0,003 10 4 0,0002  0,03 10 5

0,01
0,001
21. (GV) Determine o valor da expressão
=x+40°
22. (UNICAMP)
3
3
a) Calcule as potências: a  3 3 , b   2 , c  3 2 , d   2 .
b) Escreva os números a, b, c e d em ordem crescente.
23. A representação decimal de 0,01 é:
a) 0,03 b) 0,0001 c) 0,00000001
e) 0,000001
24. Escreva na notação científica o resultado do produto 2000 0,00000003 .
26. A expressão
a)
5
10
8  72  5 2
b)
c)
50  8  4 4
23 5 é igual a:
b)
6
c)
40
5
d) 8 10
40
e) 6 10
a)
7  17  7  17
 1
1 

c) 


3 1
 3 1
b)
3 1

32. Calcule o complemento de:
a) 25°
b) 47°
c) 37°25’
33. Calcule o suplemento de:
a) 72°
b) 141°
c) 93°15’

2x-y
35. Determine a medida do ângulo igual ao triplo do seu complemento.
27. Calcule o valor de:
3 1
x+y
34. Dado um ângulo de medida x, indique:
a) seu complemento;
f) a sétima parte do complemento;
b) seu suplemento;
g) a quinta parte do suplemento;
c) o dobro do seu complemento;
h) o complemento da sua terça parte;
d) a metade do seu suplemento;
i) o triplo do suplemento da sua quinta parte.
e) o triplo do seu suplemento;
25. Simplifique as expressões:
a) 2 3  2 12  2 75

4x-2y
x+35°
2x -10°
3
d) 0,001
3x-15°
c)
36. Calcule um ângulo cuja quarta parte do seu suplemento vale 36°.
3 1
3 1
37. Qual é o ângulo que excede o seu complemento em 76°?
2
d)
8  14  3 6  4
38. Determine o ângulo cujo suplemento excede o próprio ângulo em 70°.
39. O complemento da terça parte de um ângulo excede o complemento desse ângulo em
30°. Determine esse ângulo.
28. Determine o valor da expressão 8

2
3
 0,25  4  0,5 .
4
40. Dois ângulos estão na razão de
29. Simplifique as expressões:
4
. Se a sua soma é de 130°, calcule o complemento
9
do menor.
2 13  2 16
a) (ESPM)
2 15
b)
3
2 28  2 30
10
41. O complemento de um ângulo está para o seu suplemento assim como 2 está para 7.
Calcule a medida do ângulo.
30. Se OP é bissetriz de AOˆ B , determine x sabendo que BOˆ C  2 y , BOˆ P  y  10º e
AOˆ P  x  30 .
B
P
C
O
42. (UFES) O triplo do complemento de um ângulo é igual à terça parte do suplemento
desse ângulo. Quanto mede esse ângulo?
A
2
43. As retas r e s de cada figura são paralelas. Determine x e y.
a)
b)
c)
70°
r
r
x
r
y
3x-10°
105°
47. (UFES) Na figura, determine o ângulo α,
em graus.
4x
60°
y
y
s
3x
2x
s
s
44. (FGV) Considere as retas r, s, t, u
todas num mesmo plano, com r //s.
determine o valor em graus de 2x +
3y.
48. Na figura, o ângulo x mede a sexta parte do
ângulo y, mais a metade do ângulo z. Calcule a
medida do ângulo y.
45. Na figura, a reta ED é paralela à reta BC .
Sendo BAˆ E igual a 80° e ABˆ C igual a 35°,
calcule a medida de AEˆ D .
A
E
D
r
r
3
110°
100º

2

s
d)
51. (PUC) Na figura, a = 100° e b = 110°. Quanto mede o
ângulo x?
c)
30°
112°
50. Na figura, considere que r // s. Determine o
valor de x.
C
46. Sendo r//s, calcule o valor de  em cada caso:
a)
b)
r
z
y
49. Calcule os ângulos de um triângulo, sabendo que eles são proporcionais aos números
1, 3 e 5.
B
40°
x
s
s
e)
f)
r
r
52. Calcule x e y indicados na figura.

r
B
30°
130º
80°

y
60°
110°
50°
55° 30°
70°
s

s
x
A
2
s
3
40°
E
C
53. A figura mostra um triângulo ABC isósceles de
base BC . Sendo BD bissetriz de ABˆ C , CD
bissetriz de ACˆ B e BAˆ C  80 , calcule o
valor de x.
A
A
B̂  60 e
Ĉ  20 . Qual o valor do ângulo HAˆ S formado
pela altura AH e a bissetriz AS ?
59. No triângulo ABC da figura,
D
x
B
C
B
54. Na figura, BD e CD são bissetrizes dos
ângulos ABˆ C e ACˆ B . Sabendo-se que o
triângulo ABC não é isósceles e que BAˆ C
C
60. Num quadrilátero ABCD de diagonal AC , temos que ADˆ C  ABˆ C e DAˆ C  BAˆ C .
Se AB  2 y  17 , BC  x  5 , AD  3 y  2 e DC  15 , mostre que o triângulo
ABC é congruente ao triângulo ADC e calcule x e y.
D
x
B
C
61. Os segmentos AB e CD interceptam-se no ponto E. Se AD  BC , BAˆ D  DCˆ B ,
AE  2 y  5 , DE  4 y  2 , BE  x  5 e CE  3x  1 , prove que os triângulos ADE
e CBE são congruentes e calcule x e y.
A


E
 80º
B
62. Num quadrilátero ABCD traça-se a diagonal BD e verifica-se que ABˆ D  CDˆ B e
BDˆ A  DBˆ C . Sabe-se que AB  2 y  1 , BC  5x  2 , AD  4 y e CD  2 x  y .

Prove que o ABD é congruente ao CDB e calcule x e y.
x
C
D
63. Num ADC , AD  CD . Toma-se o ponto B no lado AC de modo que BD seja
perpendicular a AC . Sabe-se que AD  10 , CD  3 y  1 , AB  x e BC  2 y  1 .
Prove que ABD  CBD e calcule x e y.
56. Na figura, AB  AC e AD  BD  BC . Calcule a medida do ângulo de vértice A.
D
S
A
mede 100°, calcule a medida do ângulo BDˆ C .
55. Na figura, calcule o ângulo x, sendo  o
triplo de  e  o sêxtuplo de .
H
C
A
64. Seja B o ponto médio de AC . Por B conduz-se um segmento BD , perpendicular ao
segmento AC .
a) Justifique a congruência dos triângulos ABD e CBD.
b) Se AB  x , BC  2 y , AD  2 x e CD  3 y  8 , calcule x e y.
B
57. No triângulo ABC da figura, se AH é altura e BS é
bissetriz do ângulo ABˆ C , determine BSˆC , sendo
dados BAˆ H  30 e ACˆ B  40 .
A
65. Os segmentos AB e CD interceptam-se em M, que é o ponto médio dos dois
DAˆ M  2  6º ,
BCˆ M  4  3º
CBˆ M  2 ,
segmentos.
Sendo
e
ˆ
ADM  3  9º , justifique a congruência dos triângulos ADM e BCM e calcule 
S
B
58. Da figura, sabemos que AH é altura e AS é
bissetriz do ângulo BAˆ C do triângulo ABC. Se
B̂  70 e HAˆ S  15 , determine Ĉ .
H
C
e .
66. Na figura, AM  MD e CM  MB . Sabendo
que DAˆ B  20 , CBˆ A  30 e ADˆ B  46 ,
calcule as medias dos ângulos   BMˆ D e
  ACˆ B .
A
B
H
S
C
M
A
C
4
D
B
67. O ponto M é ponto médio dos segmentos distintos AB e CD . Sabe-se que
DAˆ M  2  118' , ADˆ M  2  410' , CBˆ M    908' e BCˆ M  3  544' .
Demonstre a congruência dos triângulos ADM e BCM e calcule  e .
76. (PUC) Determine o ângulo interno de um polígono regular de 170 diagonais.
77. (MACK) Num polígono regular, a medida de um ângulo interno é 150°. Determine o
número de lados desse polígono.
68. Calcule o número de diagonais de um icoságono.
78. Determine o número de diagonais de um polígono regular convexo cujo ângulo
externo vale 24°.
69. Determine o polígono cujo número de diagonais é o triplo do número de lados.
70. Determine o polígono que tem 14 diagonais.
79. (MACK) Determine o polígono regular convexo cujo ângulo interno é 7/2 do seu
ângulo externo.
71. Determine o valor de x.
a)
b)
x
80. A razão entre um ângulo interno e um ângulo externo de um polígono regular é nove.
Determine o número de lados desse polígono.
c)
2x
150°
x+15°
85°
E
P
81. Determine a medida do ângulo agudo formado pelos prolongamentos dos lados AB
e CD de um polígono regular ABCD... de 20 lados.
x-60°
82. As mediatrizes de dois lados consecutivos de um polígono regular formam um
ângulo de 24°. Determine o número de diagonais desse polígono.
130º
C
x
x-30°
120º
72. Sendo AP e CP bissetrizes, calcule o valor de x em cada caso:
B
E
a)
b)
A
x
2
x
x+20°
x+30º
60º
F
65°
3x
150°
x
83. Calcule o número de diagonais de um polígono regular ABCD... de n lados, sabendose que a bissetriz do ângulo B̂ forma com a mediatriz do lado CD um ângulo de
45º.
84. Três polígonos convexos têm n, n  1 e n  2 lados, respectivamente. Sendo de
2700° a soma dos ângulos internos dos três polígonos, determine o valor de n.
D
2x
P
x
C
140°
D
A
85. Aumentando o número de lados de um polígono em 3, seu número de diagonais
aumenta em 21. Determine o número de diagonais desse polígono.
B
73. Qual é o polígono cuja soma dos ângulos internos é igual a 1800°?
86. ABCD... é um polígono convexo regular. Sabendo-se que o ângulo
144º, determine o número de diagonais desse polígono.
74. Determine o número de diagonais de um polígono cuja soma dos ângulos internos e
externos vale 1800°.
75. (PUC) Determine a medida de cada ângulo interno de um decágono regular.
5
ACˆ D mede
GABARITO
01.
02.
03.
04.
05.
06.
07.
08.
09.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
6e9
48 anos e 56 anos
9cm e 21cm
40, 100, 220
6, 8 e 10
Michel: R$ 1200,00
Flávio: R$ 1600,00
Anderson: R$ 800,00
x=5; y=6
20, 15, 10
48 minutos
5 horas
35 dias
24 operários
alternativa c
17
a)
b) 4
16
alternativa a
alternativa c
32
18 algarismos
64
31
3600
a) a  27, b  8,
1
1
c  ,d  
9
8
b) b, d , c, a 
23. alternativa e
24. 6,0 10 5
25. a)  8 3
b)
26. alternativa b
2
38.
39.
40.
41.
42.
c) 6 2
27. a) 4 2
b) 4
1
c)
d) 2 3
3
28. 1
3
29. a)
ou 1,5 b) 2 9 ou 512
2
30. 10°
31. a) 60° b) 120° c) 120°
32. a) 65° b) 43°
c) 52° 35’
33. a) 108° b) 39°
c) 86°45’
34. a) 90º  x
b) 180  x
180º  x
c) 2(90  x)
d)
2
90  x
e) 3(180º  x)
f)
7
180º  x
x
g)
h) 90 
5
3
x

i) 3180  
5


35. 67º30’
36. 36°
37. 83°
55°
45°
50°
54°
78°45’ ou 78,75’
43. a) x  120; y  75
b) x  20; y  50
c) x  10; y  150
44. 500°
45. 115°
46. a) 72°
b) 100°
c) 52°
d) 100º
e) 20°
f) 40°
47. 144º
48. 135°
49. 20°, 60° e 100°
50. 22º
51. 35º
52. x  70; y  125
53. 130°
54. 140°
55. 50°
56. 36°
57. 110°
58. 40°
59. 20°
60. LAAo ; x  10; y  19
61. LAAo; x  3; y  2,5
6
62. ALA; x  2; y  3
63. HC; x  5; y  3
64. a) LAL
b) x  16; y  8
65. LAL;   15;   18
66.   50º ;   84
67. LAL;   19º18' ;   2810'
68. 170 diagonais.
69. eneágono.
70. heptágono.
71. a) 70° b) 90° c) 120°
72. a) 52°30’
b) 50°
73. dodecágono.
74. 35 diagonais.
75. 144º
76. 162º
77. 12 lados.
78. 90 diagonais.
79. eneágono.
80. 20 lados.
81. 36°
82. 90 diagonais.
83. 54 diagonais.
84. 6
85. 14 diagonais.
86. 90 diagonais.