Resolução do teste 4

Resolução do teste 4 (turmas A e B)
Nota: As resoluções apresentadas podem não ser as únicas corretas
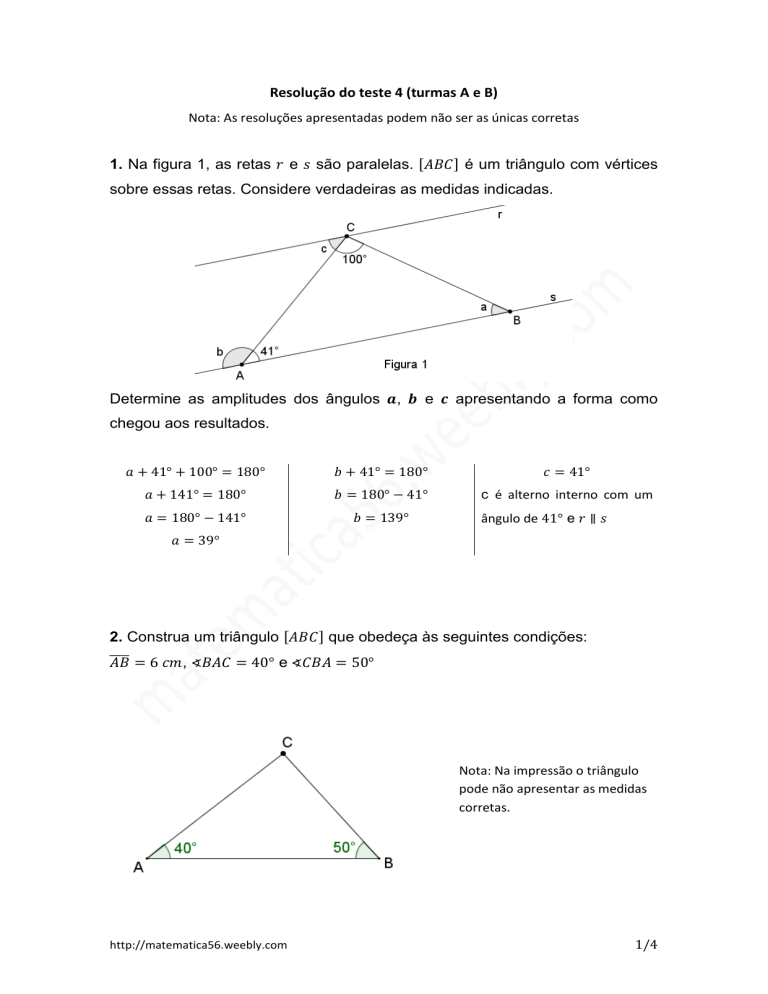
1. Na figura 1, as retas 𝑟 e 𝑠 são paralelas. [𝐴𝐵𝐶] é um triângulo com vértices
sobre essas retas. Considere verdadeiras as medidas indicadas.
Determine as amplitudes dos ângulos 𝒂, 𝒃 e 𝒄 apresentando a forma como
chegou aos resultados.
𝑎 + 41° + 100° = 180°
𝑏 + 41° = 180°
𝑐 = 41°
𝑎 + 141° = 180°
𝑏 = 180° − 41°
c é alterno interno com um
𝑎 = 180° − 141°
𝑏 = 139°
ângulo de 41° e 𝑟 ∥ 𝑠
𝑎 = 39°
2. Construa um triângulo [𝐴𝐵𝐶] que obedeça às seguintes condições:
̅̅̅̅
𝐴𝐵 = 6 𝑐𝑚, ∢𝐵𝐴𝐶 = 40° e ∢𝐶𝐵𝐴 = 50°
Nota: Na impressão o triângulo
pode não apresentar as medidas
corretas.
http://matematica56.weebly.com
1/4
3. Na figura 2, considere verdadeiras as medidas indicadas, e use-as na sua
resolução.
a) Determine a amplitude do ângulo assinalado com a letra 𝒙 e mostre como
chegou ao resultado.
𝑥 = 30° + 95°
𝑥 = 125°
b) Em relação ao triângulo da figura 2, qual das seguintes afirmações é
correta? Assinale com x a sua resposta.
O triângulo é acutângulo porque tem um ângulo agudo.
O triângulo é acutângulo porque tem dois ângulos agudos.
X O triângulo é obtusângulo porque tem um ângulo obtuso.
O triângulo é obtusângulo porque tem todos os ângulos obtusos.
O triângulo é obtusângulo porque todos os ângulos são obtusos
4. Na figura 3 está representado um paralelogramo [𝑁𝑀𝐿𝐾]. Um dos seus
O triângulo é obtusângulo porque todos os ângulos são obtusos
ângulos internos tem 108° de amplitude.
Calcule as amplitudes dos ângulos 𝒃, 𝒄 e 𝒅.
Mostre como chegou aos resultados.
𝑐 = 𝑎 = 108°. Num paralelogramo ângulos opostos
são iguais.
𝑎 + 𝑏 = 180°
𝑏 = 180° − 108°
Num paralelogramo ângulos
consecutivos são suplementares.
𝑏 = 72°
𝑏 = 𝑑 = 72°, porque são opostos no paralelogramo.
http://matematica56.weebly.com
2/4
5. Os dois lados menores de um triângulo medem 6 cm e 9 cm.
Qual é o maior número inteiro que pode medir o terceiro lado?
Justifique a sua resposta.
O lado maior tem que ser menor do que a soma dos outros dois.
6 + 9 = 15
Então o maior lado pode medir, no máximo, 14 𝑐𝑚.
6. Na figura 4 estão representados dois triângulos: [𝑄𝑂𝑆] e [𝑃𝑅𝑆].
Sabe-se que ̅̅̅̅
𝑆𝑃 = ̅̅̅̅
𝑆𝑂 e que ̅̅̅̅
𝑆𝑄 = ̅̅̅̅
𝑆𝑅
a) Justifique que os ângulos internos dos triângulos com vértice no ponto 𝑆
(assinalados na figura) são iguais.
Os ângulos são iguais porque são verticalmente opostos.
b) Mostre, usando um critério de igualdade de triângulos, que os triângulos
[𝑄𝑂𝑆] e [𝑃𝑅𝑆] são iguais.
̅̅̅̅ = 𝑆𝑂
̅̅̅̅ , 𝑆𝑄
̅̅̅̅ = 𝑆𝑅
̅̅̅̅ e 𝑅𝑆̂𝑃 = 𝑄𝑆̂𝑂,os triângulos são iguais pelo critério
Atendendo a que 𝑆𝑃
𝐿𝐴𝐿.
http://matematica56.weebly.com
3/4
7. Na figura 5 está representado o triângulo [𝑇𝑈𝑉], com algumas medidas
indicadas, que deve considerar verdadeiras.
a) Determine a amplitude do ângulo 𝑚. Explique como chegou ao resultado.
𝑚 = 69°
Num triângulo a lados iguais opõem-se ângulos iguais.
b) Classifique o triângulo quanto ao comprimento dos lados, e justifique a sua
resposta.
O triângulo é isósceles pois tem (pelo menos) dois lados iguais.
c) Com base nos valores indicados na figura, justifique que [𝑈𝑉] é o menor
lado do triângulo.
O ângulo interno no vértice T tem 180° − (69° + 69°) = 42°, logo é o menor ângulo.
Ao menor ângulo opõe-se o menor lado, então [𝑈𝑉] é o menor lado.
8. Determine o valor das seguintes expressões numéricas.
Apresente a resolução.
a) 5 × (6 + 4) − 12 =
b) 15 − 4 × 5 ÷ 2 =
= 5 × 10 − 12 =
= 15 − 20 ÷ 2 =
= 50 − 12 =
= 15 − 10 =
= 38
=5
http://matematica56.weebly.com
4/4